Participer à la recherche contre le covid

Cette section sera courte, parce que ce n’est pas du tout là où j’ai mon expertise. Je souhaite simplement donner un peu de contexte, pour que les explications qui suivent soient plus faciles à comprendre.

Qu’est-ce qu’un virus ?

Le coronavirus est donc un virus. Le « but » ultime d’un virus est de se répliquer. C’est pas forcément très recherché, mais on a fait pire, comme vous pouvez le voir sur la vidéo ci-dessous. Le virus est peut-être vivant, sûrement pas, ça dépend un peu des définitions. Et il peut être bénin ou tout dérégler dans un corps humain, ce qui n’est pas idéal, vous en conviendrez.

Un virus, et vous pouvez en lire beaucoup plus sur wikipedia ou d’autres sites, est composé d’un acide nucléique avec l’information génétique, entouré par une capside composée de protéines. Cette capside a plusieurs fonctions, comme protéger l’acide nucléique, favoriser l’attachement à une cellule et permettre de pénétrer à l’intérieur d’une cellule. Et certains virus ont une autre enveloppe tout autour, composée de lipides et de protéines. Dans le cas du coronavirus, il y a une enveloppe, et l’acide nucléique est sous la forme ARN.

Pour se répliquer, un virus a besoin d’infecter une cellule, qu’il va corrompre pour qu’elle produise les protéines nécessaires. Il réplique son génome, réassemble tout pour faire un nouveau virus, et sort de la cellule. Il ne peut aucunement se répliquer seul, sans l’aide d’une cellule.

Dans le cas du coronavirus, ou SARS-CoV-2, il y a quatre types de protéines, dont celles appelées protéine S, pour spike, protéine de pointe en français. Ce sont celles-ci qui permettent, en résumé, de pénétrer dans la cellule à infecter.

Un médicament contre les virus

L’idée d’un médicament peut être d’aider à arrêter la multiplication du virus, de l’empêcher de créer des réactions négatives dans le corps humain, ou plus simplement de l’exterminer. Et pour se faire, on va chercher dans un premier temps comment le virus performe ces actions néfastes, et ensuite, comment l’en empêcher.

On vient de le dire, le virus n’est probablement pas vivant, ne cherche pas du tout à vous tuer, mais peut le faire en cherchant à se répliquer. Ses fonctions sont entièrement déterminées par sa composition. Il ne peut s’adapter que grâce à des mutations aléatoires, et qui dans l’extrême majorité des cas, seront néfastes pour le virus. Et donc, des chercheurs très intelligents, certainement plus que moi, ont déterminé que si on connait la forme et la composition des protéines qui composent le virus et qui participe à son action, on comprendra comment il agit, et donc indirectement, comment le neutraliser.

On a été un peu vite sur la dernière phrase, en particulier sur ce qu’on apprend de la composition et de la forme de la protéine : reprenons. Un virus est composé de nombreuses protéines, comme on l’a vu plus haut. Ces protéines se replient sur elle-mêmes, ce qui va créer des sites topologiques qui vont permettre différentes fonctions. C’est illustré sur l’image juste en dessous. Ces sites vont permettre de bien positionner les réactifs (du virus et de la cellule cible) pour que la réaction correspondant à une fonction (rentrer dans la cellule, se répliquer, …) se produise.

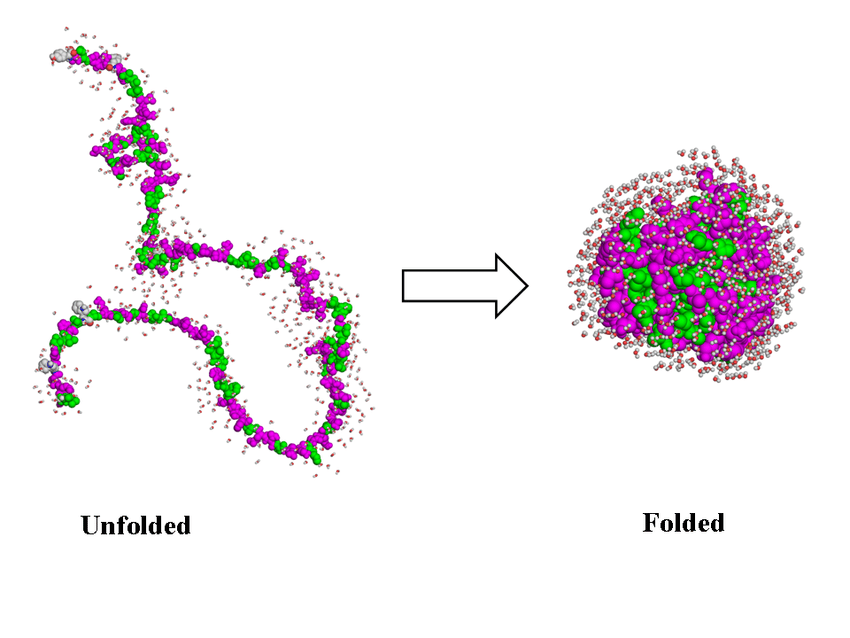
Donc, une fois que ces protéines sont repliées, l’idée est d’observer les atomes qui en forment l’enveloppe, et leur forme, trouver ce qui permet au virus d’être dangereux, et d’ensuite proposer une molécule qui s’y fixera, ou une manière de déplier et replier différemment la protéine, et ce-faisant, rendre le virus innoffensif. Facile, non ?

Du coup vous l’aurez compris, le nerf de la guerre est de simuler une protéine et peut-être une molécule additionelle pour voir son effet sur ladite protéine. Et peut-être des millions de fois cette étape, pour trouver une molécule qui pourrait marcher. Et une fois que c’est fait, recommencer sur toutes les protéines utiles du virus. La première question est donc de savoir comment on sait comment une molécule va se replier, et comment on le prédit.

Et bien ici, la réponse est à la fois simple et extrêmement complexe : la partie simple, c’est que comme pour toute chose dans l’univers, plus l’énergie est basse, plus c’est stable. Il suffit donc de calculer l’énergie de la protéine dans différentes configurations. La partie compliquée, c’est de calculer l’énergie de la protéine.

On est à l’échelle atomique, là où la physique quantique reigne sans partage. On va donc tout simplement partir de l’équation de Schrödinger.

Avec $H$ l’Hamiltonien, $\psi$ la fonction d’onde et $E$ l’énergie.

En a rarement vu équation plus simple. Bon, bien sûr, la fonction d’onde $\psi$ est vraiment compliquée à écrire pour une molécule de la taille d’une protéine moyenne. Et l’hamiltonien $H$, ou l’opérateur de l’énergie (la fonction qui va nous donner la valeur propre correspondant à un état propre) est aussi complexe, avec des termes pas loin d’être impossibles à estimer. Vous n’avez pas besoin de comprendre cette partie, comprenez seulement que $H$ va permettre de trouver l’énergie d’un système) devient aussi extrêmement complexe dans des systèmes larges (plus que quelques particules) à cause des effets multicorps.

Les écritures de $H$ et $\psi$ sont très en dehors du champ de cet article, mais modéliser quelques centaines d’atomes en utilisant cette méthode peut prendre plusieurs heures sur quelques centaines de processeurs. Il existe des algorithmes qui permettent d’atteindre l’énergie la plus basse de manière systématique, mais ils ne fonctionnent que si on a une bonne idée de ce qu’on veut trouver (ou si on est d’accord pour faire des milliers de simulations).

Résoudre tout ça, vous l’aurez compris, se fait sur des superordinateurs, et une fois de plus, vous ne pouvez pas aider. Mais qu’en serait-il si on simplifiait tout ? Si au lieu de la physique quantique, on utilisait de la physique classique ? Qu’on se contentait d’utiliser un potentiel qui donne une idée correcte sans être exceptionnelle de ce qui se passe ? Et bien dans ce cas-ci, oui, une configuration pourrait être calculée en une fraction de seconde même sur un ordinateur portable bas de gamme. Et ça tombe bien, puisqu’il faudrait calculer des centaines de milliers de cas, au bas mot. Différentes méthodes sont disponibles et seront détaillées plus tard, mais on va déjà voir les principes généraux.

Et pour ces principes généraux, on va se concentrer sur un atome (contre un éléctron en physique quantique). Si vous avez besoin d’un rappel sur le sujet, je vous invite à aller lire ce court tutoriel. On a donc un atome, entouré d’autres atomes, et ce qu’on aimerait bien savoir, c’est son énergie. Et on va l’obtenir grâce à un potentiel.

Un potentiel que vous connaissez instinctivement, c’est celui d’un ressort. Si vous tirez dessus, ça vous demande de l’énergie, et pareil si vous voulez le compresser. Il y a une position d’équilibre où l’énergie est minimale, et où le ressort est stable.

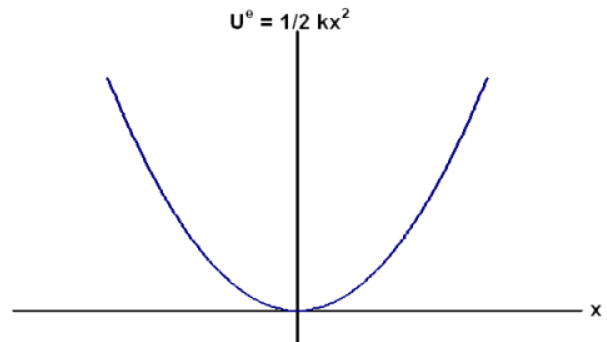
Maintenant, retournons à l’échelle atomique. Un potentiel tout simple est de mettre des ressorts entre tous les atomes.

Pour un cristal, ça donnerait quelque chose comme ça.

Ce serait donc un potentiel tout simple, que l’on appelle "binaire", qui va uniquement associer une énergie à deux éléments chimiques (qui peuvent être les mêmes) et une distance. Par exemple, si deux atomes de fer sont à une distance de 5 Ångströms, il contribueront une énergie X au total du système, et X+dX si il sont à une distance plus petite ou plus grande que 5Å. D’autres sont plus compliqués, et prendront en compte des triplets d’atomes, les angles entre les atomes, différents types d’intéraction, différentes distances maximales d’intéraction, etc. Au final, on cherche à avoir une représentation de l’énergie en tout point de l’espace, comme sur la figure ci-dessous (sauf que c’est pour un plan, parce que j’ai du mal à dessiner en 4D). Les atomes chercherait à être dans les parties ou le potentiel est le plus bas.

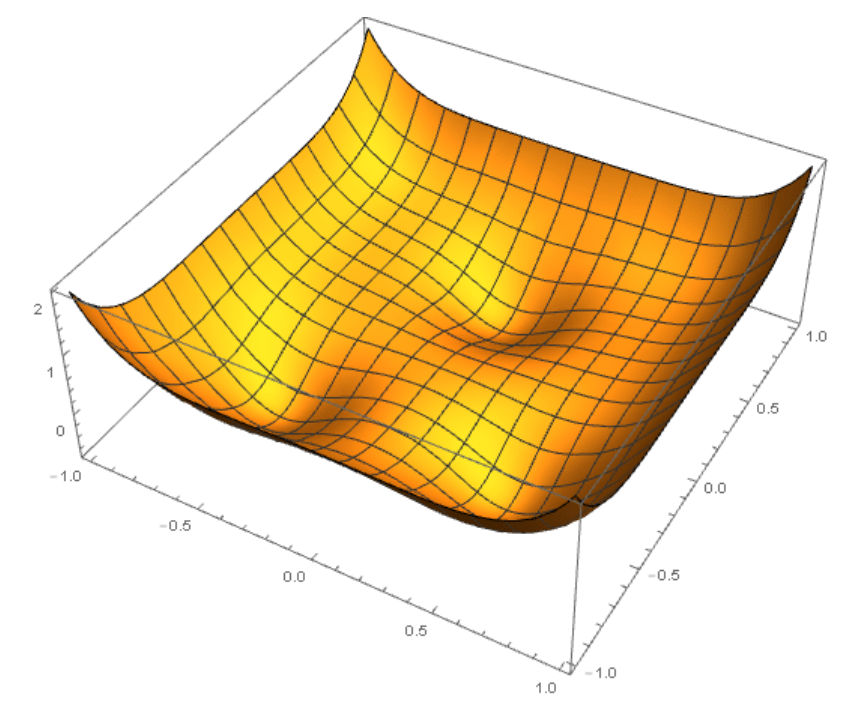
Un potentiel de bonne qualité peut prendre des années ou des décennies à être créé, et bien souvent, ce qu’on recherche, c’est quelque chose de "suffisament bon" pour donner une idée. Ensuite, les meilleures idées seront simulées avec une méthode beaucoup plus lente, mais beaucoup plus précise.

Le calcul distribué consiste à prendre une tâche gargantuesque et à la séparer en de nombreuse petites tâches. Ensuite, ces tâches sont envoyées vers les ordinateurs de volontaires, qui vont travailler dessus dès qu’ils seront oisifs. Vous pourrez ainsi utiliser votre ordinateur de manière transparente, au maximum de ses possibilités, mais quand vous irez manger ou aux toilettes, lui ne se reposera pas et travaillera pour faire avancer la science.

Il existe à ce jour plusieurs initiatives de calcul distribué, pour trouver un médicament contre le coronavirus.

Je vais ici en citer trois, parce qu’elles sont les plus connues et les plus à même d’obtenir des résultats exploitables.

Rosetta at Home

Rosetta at Home (RaH) va essayer de déterminer l’état fondamental (c’est à dire l’état avec l’énergie la plus basse, l’état dans lequel le système se met spontanément) des différentes protéines qui constituent le coronavirus. Pour ce faire, il va employer la méthode Metropolis Monte Carlo. Cette méthode part d’une configuration initiale, et essaie de changer la position de certains atomes. À chaque fois, l’énergie totale du système est recalculée, et de là, deux possibilités :

• L’énergie a baissé, et la nouvelle configuration est retenue.
• L’énergie n’a pas baissé, et soit un rejette la nouvelle configuration, soit on l’accepte avec une probabilité basse, qui dépend de l’augmentation de l’énergie.

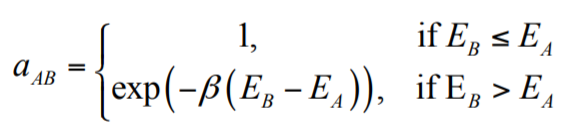
Il est utile de ne pas avoir une probabilité nulle quand l’énergie augmente pour eviter de se trouver dans un minimum énergétique local, qui passerait toutes les vérifications, mais donnerait des résultats non-explotables (voir la figure plus bas). Cette méthode est "rapide", mais ne donne aucune information sur la cinétique de la protéine, seulement sur l’état fondamental. La parallélisation extrême est faite d’une part avec des configurations initiales différentes, et d’autre part avec des algorithmes différents pour favoriser la baisse de l’énergie.

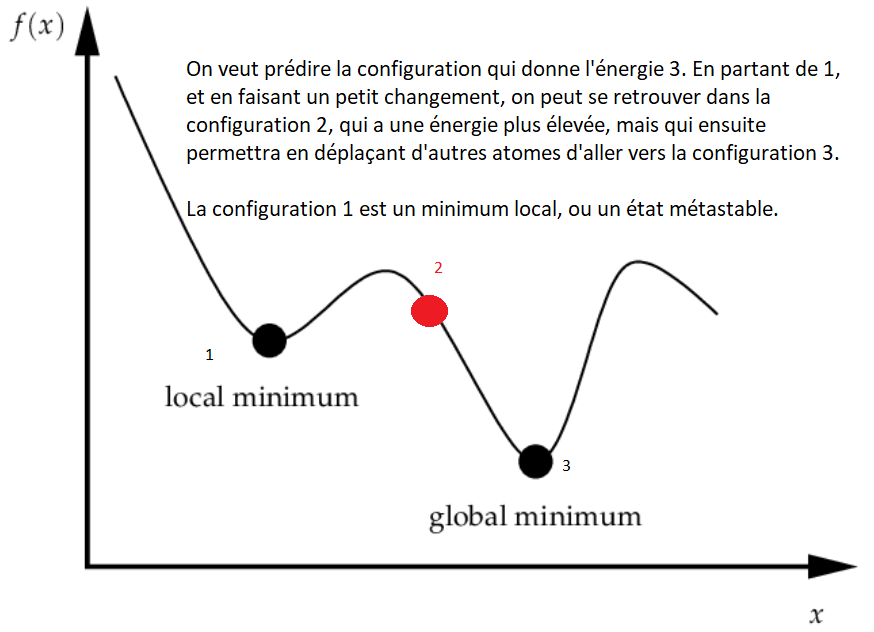
Grâce à RaH, l’état fondamental des protéines (la manière de se replier) peut être déterminé. Vous pouvez y contribuer à travers BOINC, disponible par ici.

Folding at Home

Folding at Home (FaH) va pour sa part essayer de simuler l’évolution d’une protéine avec le temps et la température. De cette manière, l’évolution des différents sites peut être connue, et une molécule qui ne serait peut-être pas efficace sur l’état fondamental pourrait l’être sur un état presque fondamental, que l’on rencontrera parfois.

Ces simulations ont pour petit nom "dynamique moléculaire", et prennent une éternité pour atteindre ne serait-ce qu’une micro-seconde. Même un millième de ça. Du coup, demander de l’aide était tout naturel. Pour aller plus loin, vous pouvez consulter les liens suivants sur les différents champs de force (plus ou moins les potentiels définis plus haut) utilisés par FaH : AMBER and CHARMM.

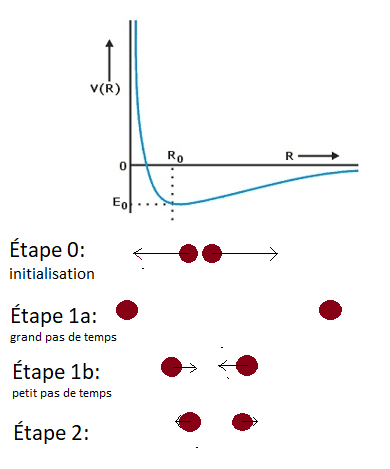
Sur l’image au dessus, vous pouvez voir comment la dynamique moléculaire fonctionne. Dans un premier temps, les atomes sont placés là où vous le souhaitez. En utilisant le potentiel, des forces sont calculées, et grace à celles-ci, on va pouvoir déplacer les atomes. Comme vous pouvez le voir sur l’étape 1a, si votre pas de temps est trop grand, les atomes vont être déplacés sur de trop grandes distances, et arriver à une situation peu réaliste : dans ce cas-ci, le lien entre les atomes est cassé, et ils sont indépendants. Par contre, plus votre pas de temps est petit, plus les positions de l’étape suivante seront réalistes. Mais ça prendra bien plus d’étapes, et donc de puissance et de temps de calcul, pour arriver à des durées qui nous intéresse. Il faut trouver le juste milieu, et en général on le fait en essayant des pas de temps différents, et en regardant quand une grandeur physique converge, c’est à dire à partir de quel pas de temps elle ne change plus assez pour justifier le coût de calcul additionel.

Pour la parallélisation, c’est plus subtil. En effet, en dynamique moléculaire, pour calculer l’étape suivante, il faut les positions et forces de l’étape présente. Le fait qu’il faille les position empêche une parallélisation temporelle simple, tandis que les forces dépendent de l’environnement et empêchent là aussi de simplement découper le système et d’en envoyer une partie à chacun, simplement.

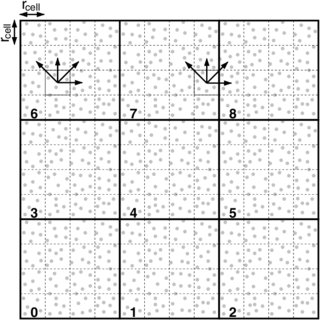
Ici, il y a une technique qui consiste a simuler beaucoup de systèmes, mais avec des vitesses initiales sur chaque atome différentes. Et ensuite, selon la fréquence de transitions (aller d’une configuration à une autre) observée, il est possible de retrouver l’écolution la plus probable de la molécule pour une durée bien plus longue que chaque volontaire ne l’aura calculée.

Vous pouvez commencer à contribuer en vous rendant ici.

World Community Grid

Le projet OpenPandemics vient apparement de commencer (NDLR: au moment où l’auteur écrit cet article, vers la mi-avril), et se base sur AutoDock. Cette méthode prédit comment une molécule va se fixer sur une structure 3D connue. Il va utiliser la méthode Force Field, mentionnée au dessus, pour cette fois essayer des millions de molécules différentes sur des structures prédéfinies. La méthode étant la même, nous ne nous attarderons pas dessus.

Tout au plus, nous mentionnerons que la structure est rigide, c’est à dire qu’elle ne se déforme pas, pour que les simulations aillent plus vite (référence). Ensuite, l’idée est de définir un score reflétant la compatibilité à partir de la simulation pour chaque molécule, et d’en essayer d’autres. Ici, des tas d’optimisations sont possibles, pour ne pas essayer les molécules de manière complètement aveugle. Par example, des algorithmes génétiques sont fréquemment utilisés, pour proposer des molécules proches de celles qui ont eu un bon score.

Pour participer, c’est par ici !