Combien de temps faut-il pour bloquer un iPad pendant 48 ans ?

Déjà pour commencer, l’iPad affiche 25 000 000 et des poussières de minutes. Vérifions donc si les 48 ans correspondent à cette valeur.

$48*365*24*60 = 25\ 228\ 800$

Nous sommes effectivement sur la bonne grandeur. Cependant, dans la vidéo on peut voir sur une image servant à illustrer les propos et on peut lire "25 536 442 minutes". Nous allons donc partir de ce nombre de minutes pour la suite de nos calculs.

$25\ 536\ 442 \div 60 \div 24 \div 365 \approx 48,6$

On est donc sur du 48 ans et demi.

Ensuite, nous allons définir une fonction qui nous donne le nombre de minutes qu’il faut attendre pour la n-ième tentative. Pour la première tentative, il faut attendre 1 minute, ensuite 5 puis 10, etc (ça augmente de 5 en 5). Ce qui se formule comme suit :

$f(n) = \begin{cases} 1,& n = 1\\ 5(n-1), & n > 1 \end{cases}$

Ensuite, on veut pouvoir définir une autre fonction qui nous retourne le temps total après x tentatives (et non seulement le temps à la x-ième tentative).

$T(x) = \sum_{k\ =\ 1}^ {x} (f(k))$

Si vous voulez un exemple plus visuel, voici l’évolution de ces fonctions :

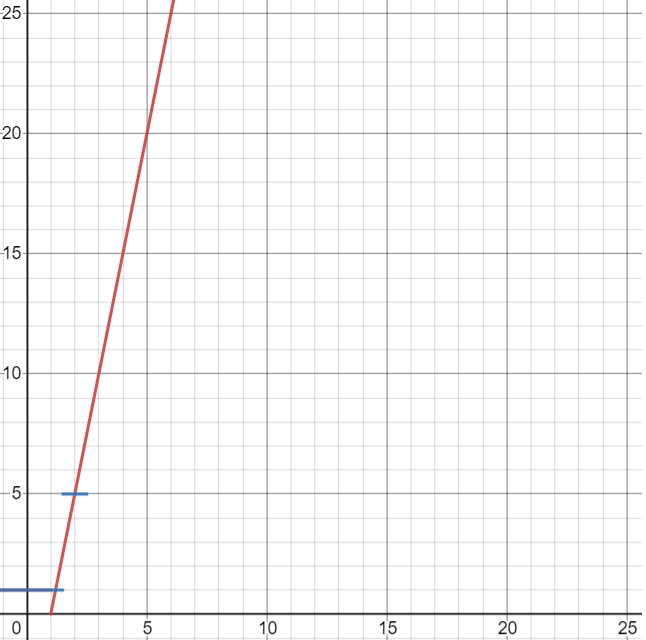
Maintenant, pour calculer le temps total pour aller jusqu’à 25 536 442 minutes, il faut savoir combien de tentatives il faudrait pour attendre ce temps. Mais l’iPad ne peut afficher ce nombre de minutes par défaut. Nous allons prendre l’arrondi à 5 juste au dessus soit 25 536 445 minutes pour que ce soit possible. Nous devons résoudre l’équation $f(n) = 25 536 445$.

$5(n-1) = 25 536 445$

$\frac{5(n-1)}{5} = \frac{25\ 536\ 442}{5} = 5107289$

$n-1 = 5107289$

$n-1+1 = 5107289+1$

$n = 5107290$

Soit plus de 5 millions de tentatives (ce fils était vraiment déterminé). Nous allons donc calculer T(5107290).

$T(5107290) = \sum_{k\ =\ 1}^ {5107290} (f(k)) = 1+5 \cdot 1 + 5\cdot 2 +...+5 \cdot 5107290 = 65\ 211\ 015\ 092\ 026$

On est sur l’ordre du billiard de minutes (juste gigantesque). Donc rien que pour arriver jusqu’à 25 536 442 minutes, il faut $65\ 211\ 015\ 092\ 026-25\ 536\ 445 = 65\ 210\ 989\ 555\ 581$ minutes. Convertissons cela en années :

$65\ 211\ 015\ 092\ 026 \div 60 \div 24 \div 365 \approx 124\ 069\ 615$

Il nous faut plus de 124 millions d’années, au moment où ce fils a commencé à essayer différentes combinaisons, nous étions en l’an $2\ 022-124\ 069\ 615 = -124\ 067\ 593$. Donc avant la sortie de l’iPad (2010) et même avant la date de fondation d’Apple (1976) ils étaient donc plutôt en avance sur leur temps . Cela s’est passé bien avant le Paléolithique (-1.76 millions d’années), et même avant les premiers humains (en -7 millions d’années ¹), pour se repérer, les premiers dinosaures sont apparus vers -230 millions d’années ².

On peut aussi se poser la question de si son fils a utilisé une méthode optimale pour dévérouiller l’iPad. Le code d’un iPad est chiffré avec un cryptage AES 256 bits, le seul moyen de trouver le bon code est d’utiliser la méthode de force brute dit "brut force" en anglais (parce que ça fait plus cool ). Cette méthode consiste simplement à essayer toutes les possibilités, le code d’un iPad est composé de 6 chiffres ¹. Nous avons donc $10^6 = 1\ 000\ 000$ possibilités. On devrait pouvoir trouver le code en 5 fois moins de tentatives que ce qu’à utiliser le fils. Ce qui signifie que le fils à entrer au moins 5 fois ou plus les mêmes nombres pour essayer de dévérouiller l’iPad (ce qui est une très mauvaise méthode). Calculons donc le temps qu’il faudrait pour essayer toutes ces tentatives : $T(1000000) = \sum_{k\ =\ 1}^ {1000000} (f(k)) = 2\ 499\ 997\ 500\ 001$

Près de 2.5 billiards de minutes (contre 65 précédemment). Et si nous voulons convertir cela en années, il suffit de faire :

$2\ 499\ 997\ 500\ 001 \div 60 \div 24 \div 365 \approx 4\ 756\ 464$.

Ce qui signifirait toujours que le fils a commencé à essayer les codes avant les premiers êtres humains.