Chaque année depuis trois ans, j’aide à organiser une marche ADEPS pour le compte de l’association caritative dont je fais partie et dont je suis par ailleurs le webmaster à mes heures perdues. Vu que notre but est de, grâce à cet événement, renflouer les caisses de l’association (parce que malheureusement, les dons n’y suffisent pas), la question est de savoir quand est-ce que nos marcheurs reviennent de leur promenade, et s’ils viennent alors consommer dans notre buvette.
Et bien que la question parait simple, la réponse demande de faire un peu de statistiques. Bref, ce billet est l’occasion pour vous comme pour moi de réviser ces statistiques en cette période estivale 🏖️
L'ADEPS est un service public belge (et plus précisément wallon, fédéralisation oblige) chargé de la promotion du sport (ainsi que de l’encadrement des formations sportives et de la gestion des athlètes). Dans ce but, des marches sont co-organisées tous les dimanches de l’année avec des associations locales. Tous les groupes et associations peuvent ainsi proposer d’organiser, un dimanche de leur choix, des promenades dans leur commune. Moyennant le respect d’un cahier des charges, l’ADEPS sponsorise l’événement et se charge de sa promotion. La marche est gratuite, mais les ventes de boissons et de nourriture permettent aux associations de rentrer dans leurs frais, voir de dégager un bénéfice comme c’est le cas ici.
Posons le problème
À la question combien l’événement nous rapporte-t-il, il est facile de donner une réponse: l’état du stock est connu et l’argent en caisse en début et fin de journée également, quelques opérations simples suffisent.
Ce que je voudrais savoir, c’est par exemple de savoir quelle est la proportion des gens qui reviennent consommer, disons, sur le temps de midi. Il ne m’est pas possible d’avoir directement accès à cette information car on ne s’amuse pas à compter le nombre de personnes qui rentrent de promenade. Par contre, je me suis amusé à relever, manuellement et toutes les heures:
- Le nombre de marcheurs qui avaient démarré une promenade durant la dernière heure (car les marcheurs doivent s’inscrire avant de commencer le parcours, question d’assurance), et
- Le nombre de boissons et de nourritures vendu durant la dernière heure (pareil, on a l’info, cette fois grâce au bon vieux système du ticket boisson™ et du guichet unique).
Autrement dit, si j’arrive à estimer quand les marcheurs reviennent, je peux aligner ces chiffres avec ceux du nombre de consommations vendues1 et avoir une réponse à ma question. À priori, c’est relativement facile et ça ne mérite pas vraiment un billet. On connait la distance des parcours (en plus se sont des multiples de 5 km) et on peut estimer qu’un marcheur marche à du 5 km/h en moyenne (vide infra). Autrement dit, on connait le temps que va prendre un marcheur pour faire le parcours, et yapluka.
Sauf que si je fais ça, j’ai de grosse différence avec la vente de consommations. Typiquement, j’estime un pic de retours vers 11h (tout les marcheurs du matin sur les différents parcours), tandis que les chiffres indiquent un pic de consommation entre 12 et 13h. Nos marcheurs seraient-ils rentrés manger chez eux ?
Avant de sauter sur les conclusions, il convient d’examiner les prémisses :
- En procédant comme indiqué plus haut, je pars du principe que tous les marcheurs comptabilisés pour une heure donnée sont partis en même temps. Dans les faits, on est plus proches de marcheurs qui partent régulièrement (ne serait-ce que parce que le nombre de personne au bureau des inscriptions limite le nombre de départ simultanés). Le profil des retours devrait donc être quelque chose d’assez étalé.
- Par ailleurs, le profil des marcheurs est très varié, et va de la famille nombreuse avec enfants et poussettes aux marcheurs chevronnés qui font ça tous les dimanches: la vitesse moyenne de ces deux groupes n’est probablement pas la même. Ce qui a pour effet d’étaler d’autant plus le profil des retours sur les longs trajets.
Bref, disons carrément des gros mots: le temps de départ d’un marcheur peut être modélisé par une distribution uniforme, (un marcheur peut partir n’importe quand dans l’intervale ), tandis que la vitesse des marcheurs peut être modélisée par une distribution normale: (en km/h). Et donc, la distribution de l’heure de retour est donnée par:
où est la distance du parcours (en km).
Ok, bon, est une distribution comme une autre … Non ?

- En partant par exemple du principe que chaque personne qui revient consomme alors une boisson. Même si on a quand même eux deux ou trois piliers de comptoir. Soit.↩
Faisons des stat's, donc
Si vous avez peur des maths, pas de problème, rendez vous à la section suivante pour les résultats
Rappels de statistique
Soit une variable aléatoire . La fonction de densité de probabilité (FDP), donne, pour un donné, la probabilité de sa réalisation (si est discrète, on parle de fréquence):
La fonction de répartition (FR) calcule la probabilité que prenne une valeur inférieure ou égale à (si est discrète, on parle de fréquence cumulée):
On peut alors remarquer que
Par ailleurs, la probabilité que soit compris entre et est donnée par:
Si , c’est à dire si est une variable aléatoire représentant le résultat d’un dé, alors:
- , c’est à dire qu’il y a une chance sur 6 de faire un 2,
- , c’est à dire qu’il y a une chance sur 3 de faire un chiffre inférieur ou égal à 2, et
- , c’est à dire qu’il y a 2 chances sur 3 de faire un chiffre compris entre 2 et 5.
Autrement dit, si je veux connaitre la probabilité qu’un marcheur parti après 9h sur un parcours de 5 km revienne entre 11 et 12h, je dois calculer , en utilisant la notation de la section précédente.
À la bourrin
Pour estimer la FDP puis la FR de , on peut s’amuser à générer un grand nombre de valeurs en choisissant au hasard une valeur pour et pour . L’histogramme des valeurs ainsi obtenues (c’est à dire la fréquence de leur apparition) sera alors une estimation de la densité de probabilité. Mieux encore, on peut demander à un ordinateur de le faire pour nous. En utilisant ensuite l'intégration de Riemman, on peut approximer la FR.
J’ai pris une estimation issue de ce papier, qui estime la vitesse moyenne d’un piéton à 1.36 m/s (=0.19 m/s) dans une zone avec large trottoir, ce rapprochant d’une situation avec faible densité de piéton, ou les marcheurs vont à leur rythme. Notez ceci dit que la valeur pourrait être encore plus élevée, comme indiqué dans d’autres articles (voir figure 8 de celui-ci ou un peu tout le papier mais en particulier la figure 5 de celui-là).
On pourrait s’amuser à discuter le fait que sur les parcours plus courts, le profil des marcheurs est plus familial, là ou les parcours plus longs sont prisés par des personnes plus aguerries, et probablement plus rapides.
Par exemple, pour un parcours de 5 km et un départ après 9h (entre 9h et 10h, donc), en tirant 1 million de valeurs au hasard à l’aide de ce code …
import numpy
import matplotlib.pyplot as plt
distance = 5 # km
t0 = 9 # h
# vitesse moyenne et déviation standard issue de https://dx.doi.org/10.1016/j.sbspro.2013.11.160
vitesse_moyenne = 4.896 # km/h
vitesse_std = 0.684 # km/h
# tire au hasard des nombres suivant la loi de probablité
# voir https://numpy.org/doc/stable/reference/random/index.html#module-numpy.random
gna = numpy.random.default_rng()
N = 1_000_000
Tr = gna.uniform(t0, t0 + 1, N) + distance / gna.normal(vitesse_moyenne, vitesse_std, N)
# calcule la fonction de densité de probabilité (FDP, ça ne s'invente pas)
FDP, bin_edges = numpy.histogram(Tr, bins=200, range=(t0,t0 + 3), density=True)
# plot
figure = plt.figure(figsize=(10, 6))
ax1, ax2 = figure.subplots(1, 2)
ax1.scatter(bin_edges[:-1], FDP)
ax1.set_ylabel('Densité de probabilité')
ax1.set_xlabel('Heure de retour')
# on "integre" la FDP pour obtenir la FR
ax2.scatter(bin_edges[:-1], numpy.cumsum(FDP) * numpy.diff(bin_edges))
ax2.set_ylabel('Fonction de répartition')
ax2.set_xlabel('Heure de retour')
plt.tight_layout()
plt.show()
… On obtient quelque chose qui ressemble à:
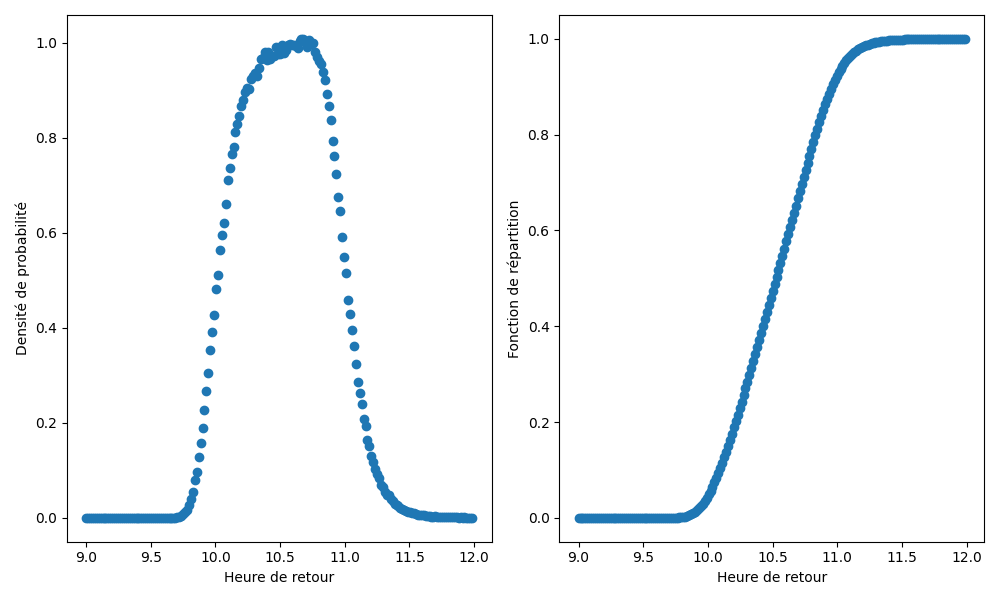
Tandis que le graphe de gauche représente la répartition des probabilités individuelles (et a un profil un peu différent de ce qu’on a l’habitude de voir, puisqu’il s’agit d’une somme de lois normales inverses), c’est le graphe de droite qui permet de répondre à des questions intéressantes. Tout d’abord, puisqu’il s’agit d’une probabilité, les valeurs de celui-ci varient entre 0 et 1. Par ailleurs, il permet par exemple d’estimer que:
- La probabilité de rentrer avant 10h30 est d’environ 48%, puisque . Il s’agit simplement de la valeur correspondant à 10.5 sur le graphe de droite.
- La probabilité de rentrer entre 11h et 12h est d’environ 8%, puisque , avec et (valeurs lues, une fois encore, sur le graphe de droite).
- S’il y a des marcheurs qui sont partis peu après 9h et qui marchent vite, ils peuvent arriver avant 10h: .
Plus de subtilité, donc plus de maths
Il est tout de fois possible d’obtenir des résultats plus précis en arrêtant de jouer aux dés et en sortant du papier et un crayon. Tout d’abord, on peut remarquer que pour ce qui est de la vitesse, on calcule en fait une distribution normale inverse, donc il est possible de connaitre la FDP.
Soit une variable aléatoire et soit une seconde variable aléatoire définie comme , on a que la FR de est donné par:
Et dès lors, en utilisant la dérivation de fonction composées,
Autrement dit, la FDP pour une loi inverse normale, que je vais noter , est:
On peut ensuite gérer le produit d’une variable aléatoire par une constante:
Soit une variable aléatoire et soit une seconde variable aléatoire définie comme avec , on a que la FR de est donné par:
Et donc, en dérivant,
Et donc, on peut trouver la FDP pour le temps de parcours [noté plus haut] comme:
Et finalement, si on veut une expression pour la FDP de , il va falloir additioner et une distribution uniforme sur .
Soit deux variables aléatoires et , indépendantes, et soit une troisième variable aléatoire définie comme , la FDP est donnée part le produit de convolution des FDPs de et :
La démo est un peu plus compliquée, mais suis le principe de "travailler sur la FR puis dériver pour obtenir la FDP" qu’on a vu avant.
Autrement dit, pour évaluer la FDP de , on doit évaluer
où j’ai utilisé le fait que la FDP de est de zéro en dehors de . Malheureusement, évaluer cette intégrale est un petit peu au delà de mes compétences, d’autant vu la forme de qui n’est pas une "simple" Gaussienne. Notez que c’est néanmoins possible pour la somme de distributions plus simples. Je vais donc opter pour une convolution numérique issue des méthodes de nos amis de la manipulation du signal.
En utilisant ce code implémentant la formule ci-dessus pour , on peut obtenir le résultat suivant:
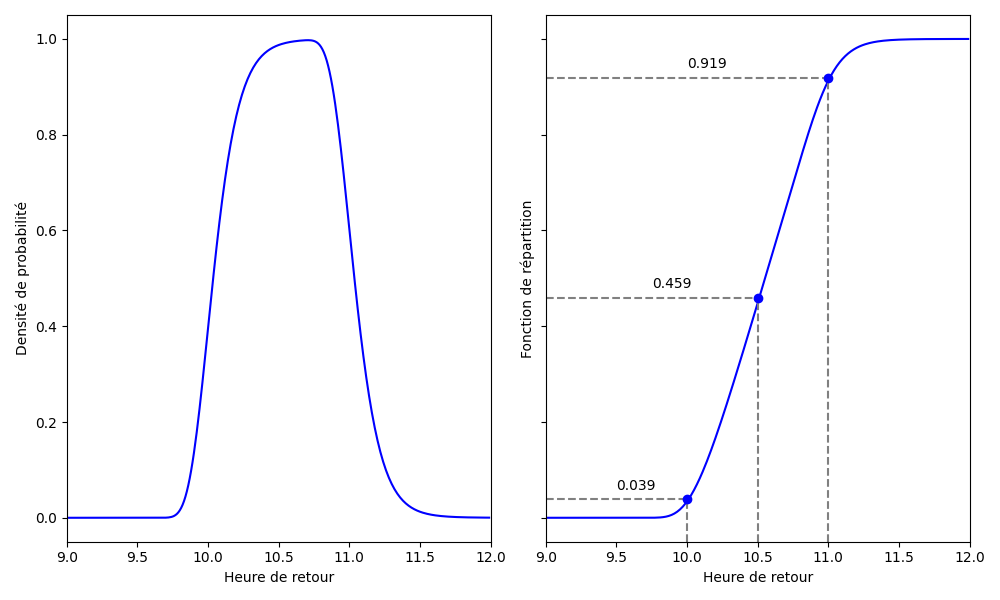
On constate que cette approche donnne des résultats équivalents à la précédente, quoi que plus rapidement et de manière un peu plus précise. Et que la forme de la FDP n’est définitivement pas commune
Ça y ressemble et on pourrait imaginer modéliser le nombre de marcheur revenant de marche avec, mais ce n’est pas exactement les mêmes prémisses.
Et donc ?
Grâce aux quelques développements de la section précédente, on sait évaluer la probabilité qu’un marcheur rentre dans un certain intervalle de temps. Voyons ce que ça donne avec les 4 parcours de la marche:
| Période | 5.6 km | 10.7 km | 16.0 km | 20.0 km |
|---|---|---|---|---|
| 0.9 | 0 | 0 | 0 | |
| 81.5 | 3.5 | 0 | 0 | |
| 17.6 | 70.7 | 5.4 | 0 | |
| 0 | 25.2 | 59.2 | 15.4 | |
| 0 | 0.6 | 32.1 | 56.5 | |
| 0 | 0 | 3.1 | 24.1 | |
| 0 | 0 | 0.2 | 3.5 | |
| 0 | 0 | 0 | 0.4 | |
| 0 | 0 | 0 | 0.1 |
Les chiffres correspondent à peu près à l’estimation qu’on aurait pu faire en utilisant simplement la distance et la vitesse moyenne (à savoir qu’un parcours de 16 km prend à peu près 3h), mais la distribution obtenue tient donc compte des départs différés et du profil de vitesse des marcheurs.1 Dit autrement, si on compte que 20 marcheurs se lancent sur le parcours de 16 km entre 9h et 10h, on aura statistiquement, 1 marcheur (motivé !) qui reviendra avant midi, 12 qui reviendront entre midi et 13h, et les 7 derniers reviendront après 13h.
Bref, si on additionne tout ça en utilisant le nombre de départs, on obtient ceci:
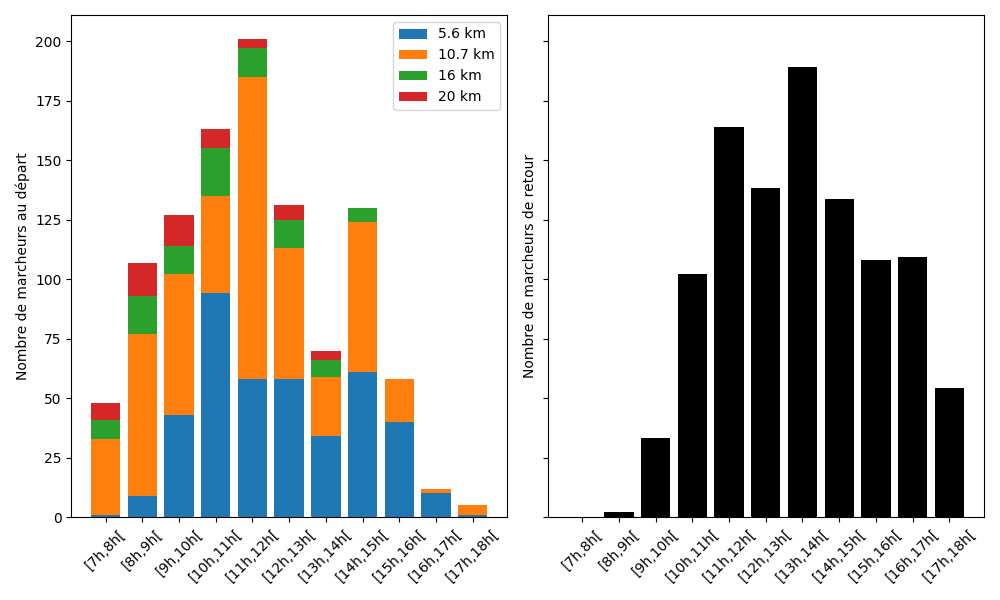
On peut observer différentes choses sur ce graphe. En vrac, que 80% de nos marcheurs viennent en matinée (avant 12h) pour faire des longs parcours (et sont plutôt motivés, avant 9h!), mais que les retours sont plutôt étalés sur le midi et l’après-midi (11h-17h). Il y a également un petit rebond des départs en début d’après-midi (après 14h, généralement pour des parcours plus court) qui vient s’ajouter à la vague des retours de milieu/fin de l’après-midi. On observe également qu’il y a des gens qui la joue stratégique en partant un peu avant midi pour éviter le rush. Manque de pot, 2h plus tard, les pains saucisses avaient bien diminué2
Plus qu’à comparer avec les chiffres de vente (mais, au doigt mouillé, je dirais qu’environ 25% des gens consomment ensuite).
Eeeeeeeeeeeeeeeeeeet … Tout ça pour ça, en fait
Prenez-le comme moi qui m’amuse un peu avec les chiffres (j’aime bien les statistiques) sans trop de prétentions non plus (d’ailleurs, si j’ai fait des bêtises, n’hésitez pas à me le signaler).
Et sinon, faites du sport, c’est bon pour la santé.
L’icone du billet est issue d’une image de Silvia Natalia sur the Noun Project
