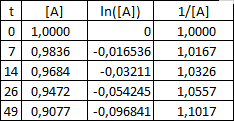
Dans mes données j’ai en fait beaucoup plus de A que de E ce qui semble logique vu qu’il faut une toute petite quantité de catalyseur, non?
Ah oui ! Nan mais c’est logique t’as raison pour un catalyseur ces approximations ne sont pas valables. 
j’ai pas bien reflechis.
Si j’avais tes valeurs j’pourrais mieux te guider j’pense, par ce que sans valeurs la seule manière de faire à ma connaissance est assez longues… Et je ne suis pas sûre qu’ici ça nous mêne quelque part :
Tu écris toutes tes équations étapes élémentaires par étapes élémentaires :
$$\mathrm{ A + E \xrightarrow[]{k_{1}} AE}$$
Dès lors ton adduit $\mathrm{AE}$ va pouvoir subir deux nouveaux équilibres.
Régénérer le catalyseur en se dissociant du réactif.
$$\mathrm{ AE \xrightarrow[]{k_{-1}} A + E}$$
Régénérer le catalyseur en donnant le produit d’interet.
$$\mathrm{ AE \xrightarrow[]{k_{2}} B + E}$$
Ensuite on devrait écrire les vitesses de chaques étapes :
$$\mathrm{v_1 = k_1 [A][E]}$$
$$\mathrm{v_{-1} = k_{-1}[AE]}$$
$$\mathrm{v_2 = k_2 [AE] = v_{tot}}$$
Ensuite il faut réussir à réunir les termes par rapport aux dérivés temporelle qui nous préoccupent. Par exemple la création de $\mathrm{[AE]}$ se fait grâce a $\mathrm{v_1}$, mais à cause des vitesses $\mathrm{v_{-1}, v_2}$ on va perdre du $\mathrm{[AE]}$ :
$$\mathrm{\dfrac{d[AE]}{dt} = v_1 - v_{-1} - v_2}$$
$$\mathrm{\dfrac{d[E]}{dt} = v_{-1} - v_{1} + v_2}$$
Si ton adduit catalyseur-réactif est très labile, on peut considérer l’approximation des états quasi-stationnaires. En gros ça nous permet d’écrire la chose suivante, car on considère que la réactivité de cette espèce est ultra-rapide, donc elle arrive en même temps qu’elle disparaît :
$$\mathrm{\dfrac{d[AE]}{dt} = 0}$$
$$\mathrm{0 = v_1 - v_{-1} - v_2}$$
$$\mathrm{v_{-1} + v_2 = v_1 }$$
$$\mathrm{v_{tot} = v_2 = k_2[AE] }$$
Donc on recherche l’expression mathématique menant à $\mathrm{[AE]}$ :
$$\mathrm{v_{-1} + v_2 = v_1 }$$
$$\mathrm{k_{-1}[AE] + k_2 [AE] = k_1 [A][E] }$$
$$\mathrm{[AE] (k_{-1} + k_2) = k_1 [A][E] }$$
$$\mathrm{[AE] = \dfrac{k_1}{(k_{-1} + k_2)} [A][E] }$$
On reprend l’expression de notre vitesse totale :
$$\mathrm{v_{tot} = k_2[AE] = \dfrac{k_2k_1}{(k_{-1} + k_2)} [A][E]}$$
Sachant que l’ordre global correspond à $\mathrm{m+n}$ :
$$\mathrm{v_{tot} = \dfrac{k_2k_1}{(k_{-1} + k_2)} [A]^m[E]^n}$$
$$\mathrm{[A]^m[E]^n = [A]^1[E]^1}$$
$$\mathrm{m+n = 2}$$
)
