Bonjour,
Considérons un modèle stochastique à un paramètre à valeurs réelles. Autrement dit, une variable aléatoire à valeurs réelles et paramétrée par un réel. Informatiquement, on aurait quelque chose de ce genre :
1 2 3 | def model(p, seed=None): random.seed(seed) return p * random.random() |
Considérant ce modèle comme une boîte noire, je souhaite étudier l’influence de $p$ sur le résultat. En particulier, je me pose deux questions :
- Comment évolue la sortie en fonction de $p$ ?
- Comment se comporte mon modèle pour $p$ suivant telle distribution (par exemple $\mathcal N(10, 1)$) ?
Comme mon modèle a en fait deux paramètres, je travaille dans un plan et peux mener mon exploration de multiples façons :
- Pour $p$ fixé, faire varier la seed
1 2 3 4 5 | seed | x x x | x x x | x x x |_x__x____x___> p |
1 2 3 4 | outputs = { p: [model(p) for _ in range(N_RUNS)] for p in [1, 4, 10, 11] } |
- Pour la seed fixée, faire varier $p$
1 2 3 4 5 | seed | x x x x x | | x x x x x |_____________> p |
- On fait varier les deux
1 2 3 4 5 | seed | x x | x x x | x x x |_x__x____x___> p |
1 2 3 4 | outputs = { p: model(p) for p in normal(10, 1, size=n) } |
Et j’ai du mal à déterminer dans quel cas quelle approche est souhaitable ou non. Déjà, cela fait-il sens de modéliser l’aléatoire par un axe réel que je peux explorer ou devrais-je simplement considérer que je n’ai que l’axe de $p$ ?
Merci.
+0
-0



 Faire 100 essais avec une graine fixe, ce serait choisir une graine puis lancer ton test 100 fois. Là, avec ta fonction
Faire 100 essais avec une graine fixe, ce serait choisir une graine puis lancer ton test 100 fois. Là, avec ta fonction 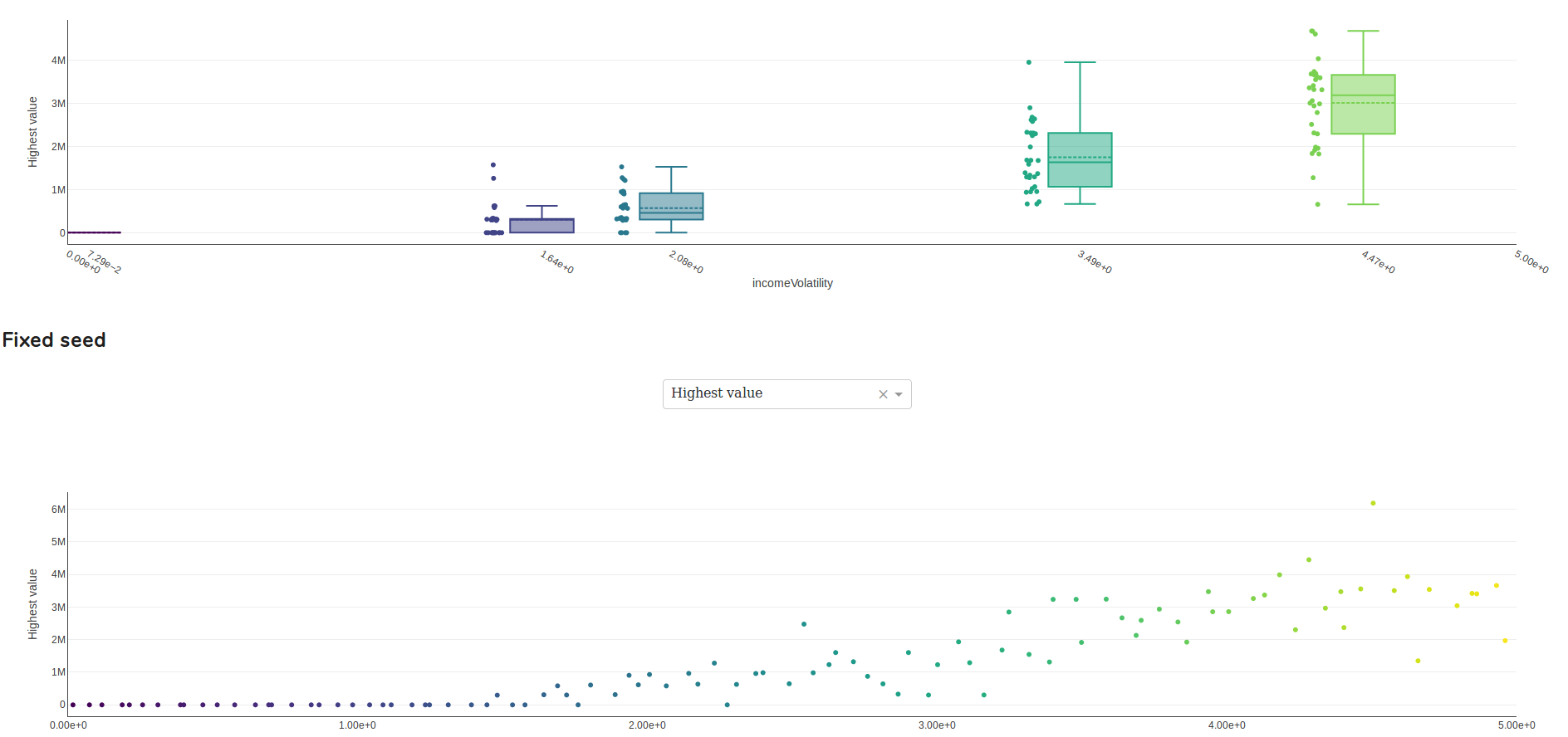
 Je ne peux que te recommander de fouiller internet avec le mot-clé
Je ne peux que te recommander de fouiller internet avec le mot-clé