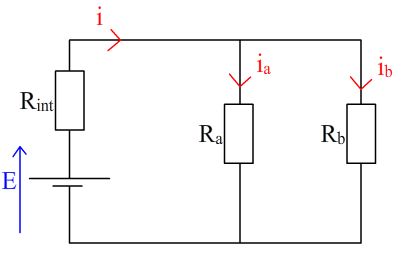
Problème de calcul d'une résistance interne

a marqué ce sujet comme résolu.

Bonsoir, je cherche à calculer la résistance interne d’une alimentation grâce à la formule Rint = (E-U)/I (avec E la tension à vide)

J’ai E = 19,4V Sachant que mes résistance ne supportent pas plus de 0,25W je mets une résistance de 3,3K ohms Ce qui nous donne théoriquement P=19,4^2/3300=0,114W < 0,25W

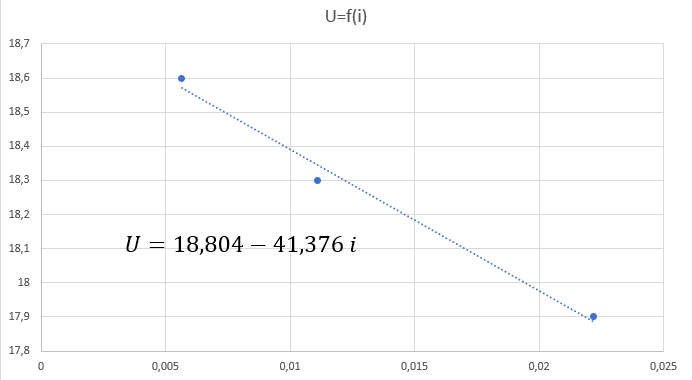
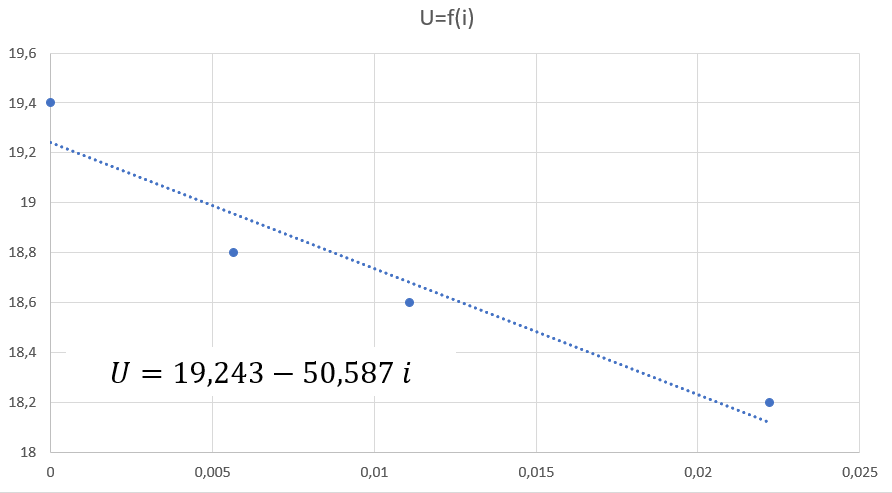
Je mesure l’intensité et je trouve I=5,65mA puis je mesure la tension U=18,6V Ce qui nous donne Rint = (19,4–18,6)/0,00565 = 141,6 ohms

Pour vérifier je répète l’experience en rajoutant des résistances en parallèle :

  • Pour 2R de 3,3k omhs en // soit R = 1,65k ohms : U = 18,3 et I = 11,1mA Donc Rint = 99ohms

  • Pour 4R de 3,3k ohms en // soit R=825 ohms U = 17,9 et I = 22mA Donc Rint = 68,2 ohms

On remarque que la résistance change à chaque fois… Auriez vous une idée de la raison pour laquelle cela se produit ou des erreurs que j’ai commises dans ma démarche.

Mercie de votre attention !

+0 -0

Si on reformule ta manière de faire, il y a forcément un soucis. Tu reproche à ta formule de te donner, pour chaque UiU_i différent, un R_{int} différent lui aussi.

Rint=E−U1i=19,4−18,60.00565R_{int} = \dfrac{E-U_1}{i} = \dfrac{19,4-18,6}{0.00565}
Rint=E−U2i=19,4−18,30.0111R_{int} = \dfrac{E-U_2}{i} = \dfrac{19,4-18,3}{0.0111}
Rint=E−U3i=19,4−17,90.0111R_{int} = \dfrac{E-U_3}{i} = \dfrac{19,4-17,9}{0.0111}

Entre les deux premiers, ton intensité ii est presque la seule à changer. Ton résultat forcément ne pourra pas donner :

19,4−18,60.00565≈19,4−18,30.0111\dfrac{19,4-18,6}{0.00565} \approx \dfrac{19,4-18,3}{0.0111}

Entre les deux derniers, ton potentiel UU est le seul à changer. Ton résultat forcément ne pourra pas donner :

19,4−18,30.0111≈19,4−17,90.0111\dfrac{19,4-18,3}{0.0111} \approx \dfrac{19,4-17,9}{0.0111}

Donc ce n’est pas du coté mathématique que ça bug. Le problème vient de l’exploitation des données à mon avis. J’ai vérifié tes résistances en parallèles, ton calcul de la résistance total est bon.

+0 -0

Pour la troisième mesure mea culpa j’ai fait une faute de frappe, ce n’est pas 11,1mA mais 22mA (logique on divise la résistance par deux donc on double le courant)

J’ai refais mes mesures de tension et j’obtiens 18,8 18,6 et 18,2

+0 -0

Premier essaie

Du coups bah j’ai tracé tes trois premières valeurs (du poste original), la courbe ainsi obtenu donne une belle droite :

On en tire l’équation de droite :

U=E−Rinti=18.804⎵E−41.376⎵RintiU = E-R_{int}i = \underbrace{18.804}_{E} - \underbrace{41.376}_{R_{int}} i

Avec les nouvelles valeurs

Si j’essaye de forcer la main avec les trois dernières tensions que tu m’as filé, et que je rajoute E=19.4VE=19.4V à i=0Ai=0\;A, j’obtiens ceci :

U=E−Rinti=19.243⎵E−50.587⎵RintiU = E-R_{int}i = \underbrace{19.243}_{E} - \underbrace{50.587}_{R_{int}} i
+0 -0

Generalités

Intuitivement je dirais que si on a un système "boite noire", on ne sait pas comment ça marche, mais on aimerai avoir accès à un truc inconnu dedans, il va falloir résoudre ça avec toutes les expériences mis à disposition.

Lorsque l’on souhaite en savoir plus sur une boite noir, on y rentre des paramètres (tes différentes résistances) on y analyse ce qui se passe en sortie (courant et potentiel obtenues). Et lorsque l’on fait ça assez de fois, on obtient un résultat cohérent avec la réalité intrinsèque de la boite noire.

En chimie quand on ne connait pas la réaction, on peut être amené à changer de type d’acide, de solvant, sans grande raison, juste pour voir comment le système réagit et ainsi en tirer une logique après de multiples expériences.

Dans le cas précis

La formule que tu as employé est la suivante : Rint=E−UiR_{int} = \frac{E-U}{i}, qui n’a rien de différent avec U=E−iRintU = E-iR_{int}. Donc ton équation était juste ! Mais inéluctablement, tu l’auras remarqué, les valeurs ponctuelle que tu obtenait n’étaient pas constante, il te fallait obtenir une moyenne.

D’où la régression linéaire d’Excel ici, qui a fait tout le travail pour determiner le coefficient directeur.

PS : J’ai trouvé la méthode sur internet, à travers ce site en deux clics.

+0 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte