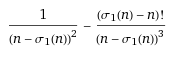Lister les valeurs entières d'un rapport mathématique

Bonjour,

Je cherche à avoir la liste des valeurs entières du rapport suivant :

$\sigma(n)$ désigne la somme des diviseurs de n (n compris).

On remarque que si n est un nombre premier alors ce rapport vaut 2 mais ce cas ne m’intéresse pas. Je cherche d’autres valeurs entières. Par exemple avec n=27 ou n=35 on a $\sigma(n)-n = 13$ et le rapport vaut 2834329.

Je cherche à savoir s’il existe d’autres entiers que 2834329.

Un programme informatique peut-il m’aider ? En quel langage ? Car je ne vois pas du tout comment faire.

Merci à vous.

Un programme informatique peut-il m’aider ? En quel langage ?

Oui, et ça n’a pas d’importance. Note que si aucune autre valeur n’est possible, le programme ne te l’indiquera pas.

Comme je fais du python, j’ai pondu ça :

from math import *
from fractions import Fraction # Pour éviter les problèmes de précision

def div(n):
    ll = []
    for i in range(1, n+1):
        if n % i == 0:
            ll.append(i)
    return sum(ll)


print(div(27)-27) # On vérifie qu'on a bien 13
print(div(35)-35)

for i in range(2, 10000): # teste tous les entiers jusqu'à 10 000
    divi = div(i)-i
    res = Fraction(1, divi**2) + Fraction(factorial(divi), divi**3)
    if res.denominator==1 and res.numerator!=2: # Affiche quand entier et pas 2
        print(i, res)

Et on trouve

27 2834329
35 2834329
2785 35589035604432841558793821402119019737974369288452691271032789347807267225115554990629467467914966631094671912238751777896970216886087385532929840450436494478956117074317743267437410021409036173314212913427526136720547650575286748830059332599415792762724507959945387930493207626803181525024058770919483723487219028459368136723198603599151473045950159382362322059804417058262854239248692150597873025901125531528079338619230957978263655990929022565515849021263321521089105933430977253232172657373624973595146591494954737394994974778902144739323520046521710241861952517016987761007828760472886465942344213677453897216006141407713481045650524985498349152559385767071294134185254021648567736769271620928236954222395961469541301006628577161193188371066526137920038592036214927719195211119405960618808552373433293583393824257277766666746778406522158371286146246444409451316822772434815284977576599090446284212435970091290699835854402785160685974604228083983600683463792495702567463421556541962289861018878916313839054174499747695918292075303041470957081109735335290634233393969807122937348548285944360861618227025286642136758557031485493220576155709150941560522239618957210326561903529998201716887140382813461253308683183528988639267562443014932059602043102006820856298249986591748719906363082825134319129

Sauf si les fractions en python sont de fausses fractions et que je suis tombé sur une erreur d’arrondi (je ne pense pas, le module de fraction sert à ça, justement), il existe bien d’autres valeurs qui marchent.

Je ai poussé un peu plus loin (pas beaucoup, c’est long), et je trouve que 21361, 26977 et 29677 marchent, avec la même valeur que 2785.

Amusant, comme propriété.

Merci, je vais analyser ton code !

J’avais remarqué que 2834329 était premier. Peut-être que tous les entiers renvoyés sont premiers (même si ce serait étonnant) ?

Je ne sais pas s’il est possible de vérifier la primalité de ce grand nombre.

En tout cas oui c’est bizarre, je ne sais pas si c’est trivial à démontrer ?

Peut-être que tous les entiers renvoyés sont premiers (même si ce serait étonnant) ?

Non, ce nombre n’est pas premier. Sur le pourquoi du comment, il faut appeler les matheux à la rescousse. @holosmos ?

Hem, attention à la limite de caractères qu’on peut donner à WolframAlpha…

En effet il y a une limite. Je viens d’essayer ce test en ligne : https://www.alpertron.com.ar/ECM.HTM

Quand j’entre le nombre et que je mets factor il semble ne rien trouver (j’ai laissé tourner 30 minutes). Quand je remplace le 9 de la fin par un 1 par exemple il trouve directement quelques facteurs. Il y a donc des chances qu’il soit premier mais je n’en ai pas la preuve définitive.

Peut-être qu’il y a d’autres moyens car ça peut prendre longtemps.

Tiens en effet, Wolframalpha a tronqué le nombre !

@Craw Le lien que tu as mis est pour factoriser un nombre, ce qui prend plus de temps que de juste tester la primalité.

Sage donne la réponse en une fraction de seconde, le nombre n’est pas premier. En notant $n$ le nombre, on peut voir que $2^n$ n’est pas congru à $2$ modulo $n$, donc $n$ n’est pas premier.

Merci pour la réponse.

Après je ne sais pas comment expliquer pourquoi on trouve souvent les mêmes entiers. J’ai pu aller plus loin avec le code python (et en réduisant le temps de recherche en remplaçant $\sigma(n)$ par $\mu(n)$) et j’ai retrouvé le grand nombre avec des nombres proches de 36000, 41000 et jusque 50000 (je n’ai plus les valeurs exactes). Pour tous ces nombres j’avais $\sigma(n) - n = 563$

On dirait que ça marche quand $\sigma(n)-n$ est un nombre premier finissant par 3.

Bonjour à tous,

Je reviens avec de nouvelles informations. En fait il s’agit d’une reformulation de la conjecture de l’infinité des nombres de Mersenne premiers (conjecture non résolue, même si les mathématiciens pensent qu’ils sont infinis).

La formule de mon premier message est en fait $B = \frac{A}{(\sigma(n)-n)}$ avec $A = \frac{(\sigma(n)-n) + (\sigma(n)-n)!}{(\sigma(n)-n)^2}$ Donc B est un entier si A est un entier.

Or pour que A soit un entier (différent de 2) il faut que $\sigma(n)-n$ soit un nombre premier (et donc que n soit un entier naturel composé).

On ne sait pas s’il y a une infinité de $\sigma(n)-n$ premiers car cela reviendrait à prouver l’infinité des nombres de Mersenne premiers. Donc on ne sait pas s’il y a une infinité d’entiers naturels différents de 2 pour l’expression A. Par conséquent, on ne sait pas s’il y a une infinité d’entiers naturels différents de 2 pour l’expression B (celle de mon topic). Le consensus actuel des mathématiciens serait de dire que oui mais il n’y a pas de preuve définitive.

Pour ceux que ça intéresse, une démonstration que je propose utilisant le théorème de Wilson :

Soit $\sigma(n)$ la somme des diviseurs d’un entier naturel n (n compris). On cherche à savoir s’il y a une infinité de n pour lesquelles $\sigma(n)-n$ est un nombre premier.

Si n est un nombre premier alors $\sigma(n)-n = 1$, cela élimine l’ensemble des nombres premiers comme valeurs potentielles de n. Si n est pair alors $\sigma(n)-n = 1+2+...$ Si n est impair et composé alors $\sigma(n)-n = 1+...$

D’après le théorème de Wilson : $(1+2+...)$ est premier SSI $((1+2+...)-1)! \equiv -1 \pmod {(1+2+...)}$

Donc SSI $(2+...)! \equiv -1 \pmod{(1+2+...)}$

SSI $(2+...)! = k*(1+2+...)-1$

SSI $((2+...)!+1) = k*(1+2+...)$

On remarque que $\sigma(n)-n = (1+2+...)$ et $\sigma(n)-(n+1) = (2+...)$ donc en remplaçant dans l’expression ci-dessus on a :

SSI $( ((\sigma(n)-(n+1))! +1 ) = k*(\sigma(n)-n)$

SSI $\frac{( ((\sigma(n)-(n+1))! +1 )}{(\sigma(n)-n)} = k$

SSI $\frac{( (\sigma(n)-n) + (\sigma(n)-n)!)}{(\sigma(n)-n)^2} = k$

Donc si k est un entier naturel différent de 2 on a n tel que $\sigma(n)-n$ est premier. Si k = 2 on a $\sigma(n)-n = 1$ et n est premier (cas trivial).

Maintenant il faut donc montrer qu’il y a une infinité de n tels que $\frac{( (\sigma(n)-n) + (\sigma(n)-n)!)}{(\sigma(n)-n)^2}$ est un entier naturel différent de 2. Cela montrerait qu’il y a une infinité de nombres de Mersenne premiers car l’infinité de nombres de Mersenne premiers est liée à l’existence de l’infinité de $\sigma(n)-n$ premiers (on le voit en développant simplement l’expression de $\sigma(n)$).