Chimie quantique et péricyclique

Diels-Alder

Le problème exposé dans ce sujet a été résolu.

Bonjour les copinous,

C’est noël et bien sûr on révise comme des foufous :lol: … Ahah ah… ah… j’espère que ce n’est pas le cas pour tout le monde :'( … Bon du coups le nom dans le perfectionnement de la chimie organique j’ai un 'tit soucis contre intuitif que j’aimerais balayer avec l’appuis des experts :

la règle des gros ↔\leftrightarrow gros et petit ↔\leftrightarrow petit

Dans cette règle on fait intervenir les volumes les plus gros des orbitales avec les plus gros et les plus petit avec les plus petit.

En effet dans les réactions péricycliques on essaye d’expliquer la régioselectivité et la diastereoselectivité à l’aide des orbitales.

  • Diastereoselectivité expliquée par la stabilisation d’un approche endo- plutot que exo- par exemple
  • Regioselectivité expliquée avec ces notions de coefficients/volume des orbitales moléculaire

Dans cette dernière on doit étudier et prévoir le volume des orbitales selon les groupements attracteur ou donneur ramifiés sur le diène et le diènophile :

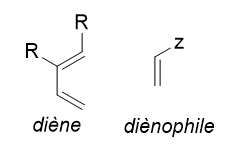
illustration
illustration

Par exemple on peut étudier la réaction suivante :

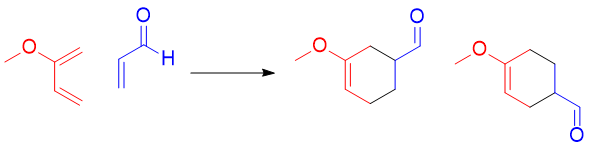
illustration
illustration

Alors on devra deviner lequel des deux est plus probable en s’essayant aux jeu de coefficient mis à disposition :

ΨOM=c1φ1+c2φ2+c3φ3+...\Psi_{OM} = c_1 \varphi_1 + c_2 \varphi_2 + c_3 \varphi_3 + ...
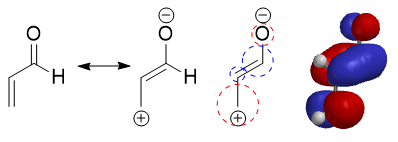
illustration
illustration

Et sur Spartan’16, cela confirmerais que sur une charge positive nous ayons plus de densité electronique. Autrement dit, une lacune electronique participe d’avantage à l’orbitale moléculaire que la charge négative ! Et là, dans ma tête ça débloque.

J’ai bien essayé de me dire, ok dans une LUMOLUMO on doit fonctionner à l’inverse que dans une HOMOHOMO et peut-être que ça a toujours un sens de parler de densité électronique avec un rapport à la mésomérie ? Et bien j’ai aussi eu de mauvaises expérience avec la simulation d’un benzaldéhyde où aucun site n’était franchement positif ni négatif…

Du coups j’aurais bien besoin d’un coups de main ! @Pierre_24 si tu passes dans le coin coin… :-°

+0 -0

Déjà, il ne faut pas oublier que les coefficients LCAO n’ont pas forcément le sens que tu entends. En particulier quand les molécules ne sont pas gentilles. Ici, t’a de la chance que les orbitales atomiques qui composent ta HOMO sont grosso modo les orbitales pzp_z, mais c’est pas donné que ce soit le cas (et à mon avis, dans tes coefficients LCAO t’a aussi des ss). Ce qui à du sens, c’est le carré de tout ça, qui te donne la densité, ici celle de trouver tes deux électrons de ta HOMO si tu prenais le carré de ton orbitale. C’est aussi grosso modo comme ça que sont calculées les charges partielles (mais évidement, ça fait intervenir toutes les orbitales occupées).

Note: j’ai essayé de faire des Diels-Alder faire un TP pour mes étudiants cette année, et j’ai vite arrêté quand je me suis rendu compte que ça marchais pas des masses, en fait. Quand on cherche un peu, on se rend compte que ça marche bien quand on fait du Hückel (étendu), plus du tout après. Et y’a une bonne raison (y’en a plus d’une, mais ici y’en a une bonne): tu part ici du principe que ta molécule est représentée par une fonction d’onde, qui est celle donnée ici par Spartan, et exploitée pour te donner la HOMO. Alors certes, mais là, t’a 2 formes de résonances ("neutre" et "zwitérioniques") relativement significatives, donc .. Deux fonctions d’ondes différentes, à priori. Dans les molécules toutes carbonées habituelles, c’est la forme de résonance "neutre" qui contribue principalement, et t’es tranquille, parce que ce que tu calcules est relativement juste. Une fois que tu tapes des hétéroatomes, t’a plus qu’à prier pour que il y aie une forme de résonance principale, et que ce soit celle que tu espères.

+0 -0

Donc toi tu dis qu’on peut mettre en relation la (cn)2(c_n)^2 avec la mésomérie du coups ? Mais c’est juste une question de modèle ?

Le problème c’est que les coeff de Spartan '16 vont dans le sens des illustrations donnés dans mes notes de cours.

Sauer et Sustmann, Angewandte Chemie International edition in English, 1980, 19, 779–807

+0 -0

J’ai du mal à te suivre … C’est les schémas pour le diene, là :o

Donc toi tu dis qu’on peut mettre en relation la (cn)2(c_n)^2 avec la mésomérie du coups ? Mais c’est juste une question de modèle ?

Blackline

Non, justement, que la mésomérie est mal décrite par une méthode de chimie quantique basée sur une unique fonction d’onde (ce qui est le cas des méthodes "de base"). Il y a bien entendu des manières de corriger ça, mais in fine, c’est pas forcément la solution.

+0 -0

Dans la publi que je cite il y a l’étude pour les diènophile aussi pardon. Mais voilà le type de modèle qu’on m’as montré et je ne comprend toujours pas comment les comprendre/interpréter. Ils vont dans le sens contraire de la mésomérie selon moi.

Là où il y a une charge positive qui PEUT apparraitre, on est censé y trouver une densité plus faible et donc :

  • Un potentiel electrostatique positif
  • un coefficient d’orbitale faible pour la contribution de cette orbitale atomique

?

Table Sauer
Table Sauer
+0 -0

Le parallèle entre l’orbitale atomique (HOMO) et la position d’une charge n’est pas forcément évident: la charge est calculée à partir de la densité électronique totale (comprenant toutes les orbitales occupées), tandis qu’une orbitale moléculaire est une représentation de la fonction d’onde correspondante, n’ayant pas spécialement de sens (son carré en a), et indiquant les endroits ou se trouvent possiblement les deux électrons qui la compose. Le lien entre la forme mésomère et le dessin de la HOMO est tentant, mais également risqué (parce qu’en vrai, une forme mésomère indique la position de la densité électronique de manière globale, pas simplement des deux malheureux électrons que tu déplaces).

Ceci sans compter qu’on est loin du monde idéal de la théorie de Huckel, ou seul les orbitales pzp_z comptent. L’orbitale que tu représentes n’est probablement pas 100% π\pi. Par contre, les résulats de la publis sont probablement issus

De plus, comme la méthode que tu utilises (et c’est pas de la faute de Spartan, c’est comme ça) représente la fonction d’onde (donc la densité électronique) par une unique fonction d’onde1, la densité électronique que tu observes est une moyenne des deux formes de résonances que tu dessines, avec, probablement, un gros impact de la forme neutre (on va pas se mentir, la forme avec deux électrons totalement délocalisés, ça existe, mais c’est faible). La publi dont est issue l’image que tu utilises en parle d’ailleurs un peu (colonne juste à côté de l’image).

  1. Un unique déterminant de Slater, en vrai.

    ↩
+1 -0

la méthode que tu utilises

En fait c’est juste à titre illustratif, mes profs m’ont donné des dessins qui ressemblent à ceux de la publi. Moi j’ai juste essayé de retrouver ces dessins, Spartan va dans ce sens.

Mais je n’arrive pas à prédire ces dessins sans logiciel c’est ça mon soucis.

Comment faire si la mésomérie ne sert à rien ? Comment prévoir la participation des lobes et de chacunes des orbitales ?

+0 -0

la méthode que tu utilises

En fait c’est juste à titre illustratif, mes profs m’ont donné des dessins qui ressemblent à ceux de la publi. Moi j’ai juste essayé de retrouver ces dessins, Spartan va dans ce sens.

C’est normal ;)

(comme je disais, Spartan doit utiliser une méthode qui est proche de celle qui a servi à générer les dessins de ta publi).

Comment faire si la mésomérie ne sert à rien ? Comment prévoir la participation des lobes et de chacunes des orbitales ?

Blackline

Autant le dire tout de suite, t’a plus de chance de retenir les dessins par coeur ^^ Objectivement, tu ne peux pas. Le mieux que t’a sous la main pour le faire, c’est Hückel, et tu devrais normalement la tuner un peu pour intégrer des atomes qui ne sont pas des carbones. Je crois me souvenir qu’à un moment, on dit aussi fuck la FMO et qu’on regarde plutôt les formes mésomères, mais c’est un peu loin dans ma tête (je me souviens plus exactement du contexte).

+1 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte