Bonjour,
Je m’intéresse un peu aux bases de la théorie des graphes mais je trouve la terminologie assez compliquée sur Internet.
Prenons par exemple un graphe (complet?) avec 5 noeuds:
Est-ce que le cardinal de ce graphe est bel et bien 5 car c’est le nombres de "segments" à l’extérieur? La longueur du chemin le plus court entre deux noeuds est bien de 1 ?
J’ai représenté ce graphe comme ceci (je ne sais pas si c’est bien ce qu’on appelle un graphe complet à 5 noeuds par contre):
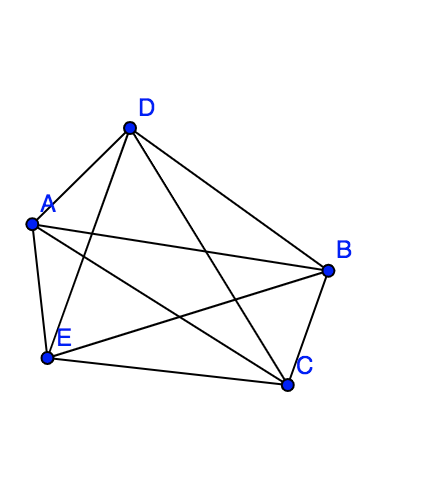
Merci d’avance pour votre aide!
+0
-0
