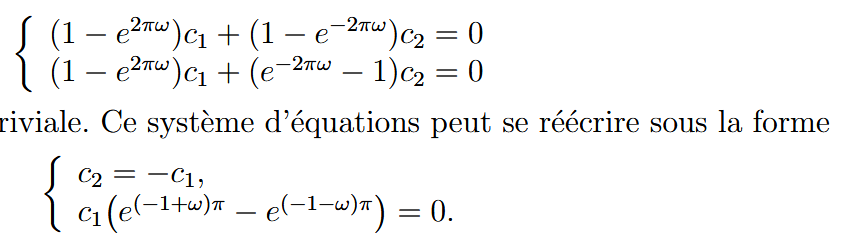Problème algèbre tout simple

Bonjour à tous !

Je coince sur comment ils ont réussi à montrer que $c_1 = -c_2$ :

ça a l’air trivial pourtant je n’ai toujours pas réussi à trouver, auriez-vous une piste ?

Si on avait $(1 - e^{2\pi\omega})c_2$ dans le deuxième terme de la première équation (c’est-à-dire, sans le signe «moins» dans l’exponentielle), ce serait effectivement trivial : faire passer le deuxième terme à droite du signe égal, puis diviser par $(1-e^{2\pi\omega})$.

Pour ton système actuel, je vois comme un problème : en faisant passer le deuxième terme de chaque équation à droite du signe égal, en multipliant par $-1$, puis en utilisant la transitivité de l’égalité, je trouve que :

$(1-e^{-2\pi\omega})c_2 = (e^{-2\pi\omega}-1)c_2.$

(Notons $(\ast)$ la relation ci-dessus.) Maintenant, quitte à supposer que $c_2$ est non-nul, on peut diviser par $c_2$ de part et d’autre de l’équation pour trouver :

$1-e^{-2\pi\omega} = e^{-2\pi\omega}-1,$

ce qui est faux en général. En effet, c’est une équation de la forme x=-x, elle ne peut être vraie que pour $x=0$. Donc, cette égalité n’est vérifiée que pour les valeurs de $\omega$ qui annulent les deux quantités de part et d’autre du signe «égal». Si tel est le cas, n’importe quelle valeur de $c_2$ est solution de l’équation $(\ast)$ !

L’autre possibilité est $c_2=0$, ce qui implique $c_1=0$, sauf pour les valeurs de $\omega$ qui annulent $1-e^{2\pi\omega}$, au quel cas $c_1$ peut prendre n’importe quelle valeur.

Je peux me tromper quelque part (je ne suis pas le meilleur du monde en calcul), mais j’ai quand même l’impression qu’il y a anguille sous roche.

(Edits : GuilOooo apprend le markdown.)

Le corrigé de mon exo doit avoir une faute probablement alors, merci !

Mmh… Si d’autres agrumes pouvaient venir confirmer que je ne me suis pas pris les pieds dans le tapis avec mes calculs, ça me rassurerait.

Ce serait possible de voir l’exercice et le corrigé complet ?

Pour $\omega$ général en tout cas la somme des deux équations montre plutôt que $c_1=0$. Et ça implique $c_2=0$.

Après je sais pas si y a plus d’hypothèses sur $\omega$

@GuilOooo : En sommant les deux égalités, on obtient $2(1-e^{2\pi\omega})c_1=0$, ce qui équivaut à $w\equiv 0[mod 1]$ ou $c_1=0$. Alors :

• Si $w\in\mathbb{N}$, pour tout $c_1$ et $c_2$, l’égalité est vérifiée
• Sinon, $c_1=0$ et $(1-e^{-2\pi\omega})c_2=-(1-e^{-2\pi\omega})c_2$, donc $c_2=-c_2$, d’où $c_2=0$

S’il n’y a pas de condition préalable sur $\omega$, donc si le cas $1-e^{2\pi\omega}=0$ n’est pas exclus, affirmer $c_1=-c_2$ semble donc faux.

EDIT: mince, doublon avec le précédent

Salut,

Pour enrichir ce que dit Holosmos, on a deux cas : oméga entier ou non entier.

Dans le cas cas entier, tous les coefficients devant les inconnues s’annulent et donc tout couple de complexes est solution.

Dans l’autre cas, seul (0,0) convient. Ça se montre très facilement par combinaison linéaire des équations du système.

Maintenant, il semblerait que le corrigé ait résolu un autre système, avec que des plus dans les exponentielles et en faisant l’hypothèse d’oméga non entier.

@CH4 : tu peux tenter de résoudre les systèmes (avec et sans altération) avec les indications pour te convaincre de ce qu’on dit.

Pour revenir à des choses simples, le 1er système est :

a+b=0
a-b=0

avec a et b … faciles à identifier.

Et donc, trivialement pour reprendre l’adverbe du document : a=0 et b=0.

Il me semblait bien que je n’avais pas les yeux tout à fait en face des trous. Merci les ami·e·s !