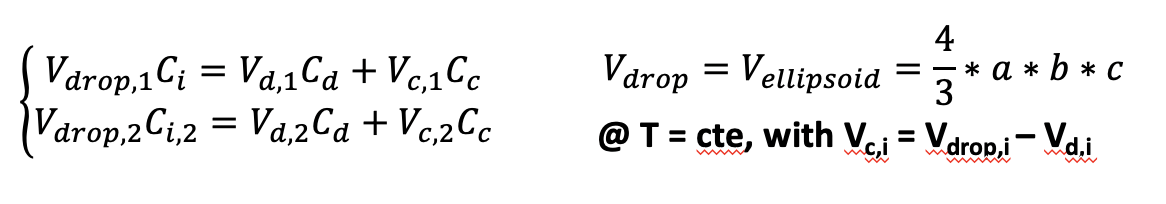Bonjour à tous,
Je dois résoudre un système d’équation linéaire très simple, 2 équations avec 2 inconnues. Mon soucis c’est que c’est basé sur des données expérimentales et donc, dans un premier temps, j’ai 4 set de données (ie. 4 équations peuvent être écrites) mais toujours pour les deux inconnues que je cherche. Plus tard, je rajouterai encore des set de données afin de pouvoir avoir un résultat robuste (que mes 2 inconnues soient proches de la réalité).
Je ne sais pas bien quelle méthode serait la plus facile à implémenter ? Évidemment avec 3 ou 4 set de données je peux remplacer et vérifier si ça fonctionne manuellement mais quand j’en aurai une dizaine (ou plus) ça va devenir long.
Avez-vous une méthode en tête qui pourrait être satisfaisante ?
Merci!