Equipartition de l'énergie : solide d'Einstein

Oui c’est cela, explication : Édit à non faut pas diviser faut mettre à la puissance.

Non, mais "presque", explication :

La fonction de partition est un facteur de normalisation.

Quand on fait la supposition que les états se repartissent selon la distribution de Boltzmann on sait que la probabilité d’être dans un état $P_i \propto e^{-\beta E_i}$. Si j’appelle le coefficient de proportionnalité $A$ et que l’on remarque que le systeme est forcement dans un et un seul état on sait que $\sum_i P_i = A \sum_i e^{-\beta E_i}= 1$.

D’où :

$A = \frac{1}{\sum_i e^{-\beta E_i}}$

On appelle $Z$ la fonction de partition et elle vaut $1/A = \sum_i e^{-\beta E_i}$.

Il est important de voir que les $i$ désignent le $i-eme$ etat. Les sommes sur $i$ sont donc des sommes sur tous les états.

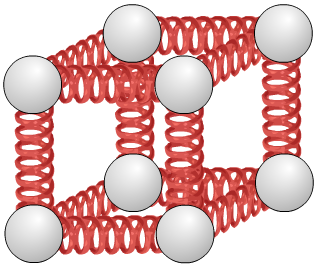
La fonction de partition que tu donnes est la fonction de partition de l’oscillateur harmonique en 1D. Dans le cas 3D de ton cristal il y a, avec une approximation aux petites perturbations, 3 oscillateurs harmoniques découplé (indépendant) selon $x$, $y$ et $z$ (c’est une approximation car en vérité ils ne sont pas découplé et les états sont plus compliqué).

Edit: Voila la bonne version (c’était bien sur une multiplication et non une addition).

Donc qui dit 3 oscillateurs indépendants dit qu’il existe $N_x \times N_y \times N_z$ états :

$Z = \sum_i e^{-\beta E^x_i} \times \sum_j e^{-\beta E^y_j} \times \sum_k e^{-\beta E^z_k}$

J’ai pris des indices différents $i,j$ et $k$ juste pour montrer qu’on somme pas sur les même états ($i$ sur les états de l’oscillateur selon $x$, $j$ sur $y$ et $k$ sur $z$) mais mathématiquement c’est équivalent. De plus comme on fait la supposition que les oscillateurs selon $x$, $y$ et $z$ sont les même (même potentiel, ie même "raideur") on sait que $E^x_i = E^y_i = E^z_i =E_i$. Finalement on peut donc écrire :

$Z = (\sum_i e^{-\beta E_i})^3$

Par contre sur un cristal anisotrope on a $E^x_i \neq E^y_i \neq E^z_i$, on doit donc rester avec le produit initial.