Gestion de dépendances

Hello,

Je sens que je suis face à un problème classique, mais impossible de trouver de l'état de l’art à ce sujet, probablement faute à avoir pile poil les bons mots clés.

J’ai des chaines de transformation avec des résultats intermédiaires qui sont cachés sur disque, et même si le produit intermédiaire n’est plus là, et qu’il y un produit plus avancé dans les transformations, ça me va très bien, inutile de régénérer le produit intermédiaire.

Avec des gros mots, cela donne que j’ai un Graphe Acyclique Direct (DAG), qu’il est déjà réduit. Voire même si j’ai bien compris, j’ai un joli polytree…

Mon objectif est d’enregistrer les tâches de transformations qu’il reste à réaliser, et de ne pas refaire ce qui n’est plus utile. Mon impression est qu’avec une approche naïvo-simple où je trie topologiquement mon DAG, si j’enregistre directement mes tâches, je vais me retrouver à faire des trucs inutiles alors que je devrais pouvoir être capable de simplifier en amont — typiquement si je suis la démarche de ce notebook, ou l'exemple de base chez Dask.

Un petit dessin pour illustrer la situation.

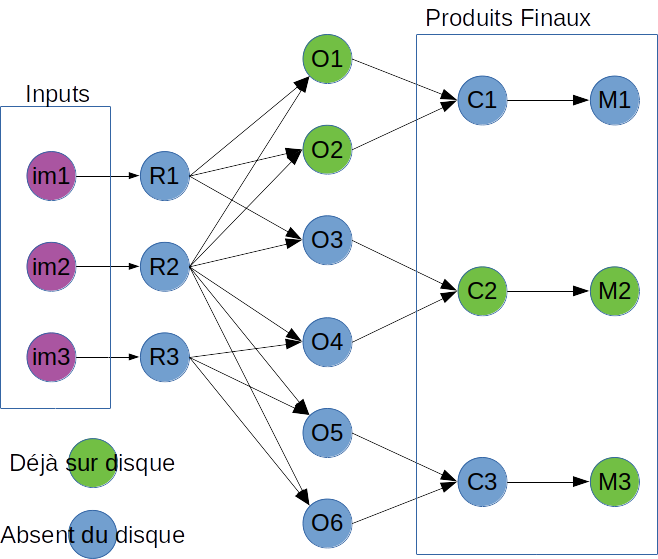
Avec les hypothèses suivantes:

• im_i sert à produire R_i
• La production de O1 nécessite R1 et R2
• (à partir de mes images d’inputs je suis capable de générer le graphe générique complet)
• en vert sont les choses qui sont déjà produites et sur disque
• en bleu les choses qui ne sont pas là (jamais été là, ou effacé, peu importe)
• Le produits finaux sont nécessaires,
• les trucs du milieu n’ont pas besoin d’être produits, voire c’est mieux de l’éviter s’ils ne servent plus.
• (le nettoyage est hors périmètre)

Ce qui veut dire que :

• C1, M1 et C3 doivent être produits ici.
• toutes les dépendances de C1 sont là (O1 et O2), donc il ne faut pas déclencher le calcul de leurs tâches amont, en particulier R1
• C2 et M2 sont là, donc nul besoin de déclencher O3 ni O4, et donc vraiment pas besoin de R1
• C3 doit être produit, donc O5 et O6 aussi et donc R2 et R3 — même s’ils n’étaient pas nécessaires pour C1 ou C2.

C’est à dire qu’après simplifications, mon nouveau DAG devrait être

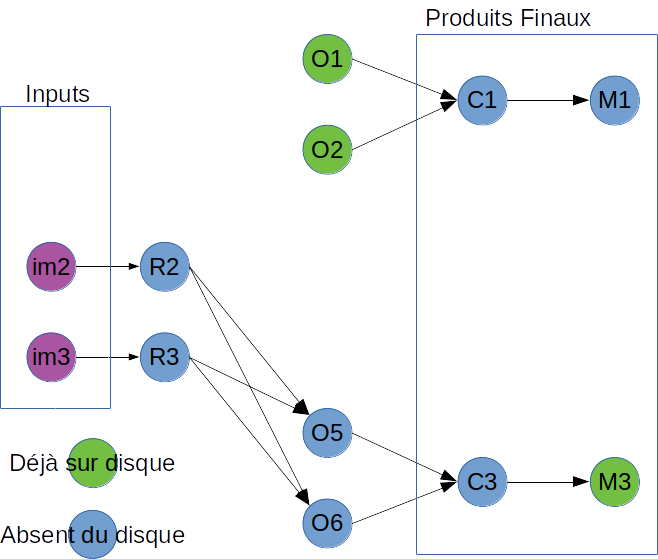
J’ai raté/oublié quoi d’évident, ou (super?) connu ?

Salut,

J’ai déjà eu ce genre de problématique, et le mot clé qui revient souvent est pipeline. Ça pourrait t’aider dans tes recherches. J’avais un besoin autour d’un outil très spécifique, donc malheureusement, les résultats de mes recherches ne te seront pas très utiles.

Et pour ce que tu veux faire, il ne faut pas nécessairement trier, mais seulement remonter le graphe et mettre à "à faire" les tâches devant être mises à jour.

C’est exactement ce que fait un système de build. As-tu envisagé d’utilister un système de build au lieu d’en réimplémenter un toi-même ? Tu peux prendre ton graphe de dépendance, générer dynamiquement un Makefile qui le représente, et appeler make; par exemple (ou ninja, etc.).

Sur l’algorithme: une façon de faire qui me semble assez naturelle est de partir des sorties, et d’avoir un algorithme récursif: pour construire chaque nœud, s’il est déjà à jour tu t’arrêtes, sinon tu construis récursivement les dépendances et tu le génères (ou, version pré-traitement, tu le marques comme devant être reconstruit).

Merci pour vos réponses.

J’ai déjà eu ce genre de problématique, et le mot clé qui revient souvent est pipeline. Ça pourrait t’aider dans tes recherches. J’avais un besoin autour d’un outil très spécifique, donc malheureusement, les résultats de mes recherches ne te seront pas très utiles.

pipeline ne m’a pas beaucoup recadré dans mes trouvailles à part me faire sortir airflow encore plus. C’est ça ton framework ?

C’est exactement ce que fait un système de build. As-tu envisagé d’utiliser un système de build au lieu d’en réimplémenter un toi-même ? Tu peux prendre ton graphe de dépendance, générer dynamiquement un Makefile qui le représente, et appeler make; par exemple (ou ninja, etc.).

Je sais bien que c’est ce qu’ils font d’où que j’espérai pouvoir trouver une lib ou un algo prêt à l’emploi qui correspond à cela. Après, je suis sur des systèmes qui détestent les micro-accès au disque. D’où que je pars pars d’un pré-scan du disque pour maintenir les états suivants en mémoire et minimiser les accès inutiles si je le peux. Je tenais aussi à éviter les allers-retours entre Python et bash vu que les process des transformations seront parallélisés ensuite avec Python, potentiellement sur des nœuds de calcul multiples.

Sur l’algorithme: une façon de faire qui me semble assez naturelle est de partir des sorties […]

C’est ce que j’ai commencé à faire. Partir de la fin pour identifier ce qui doit être généré.

Comme je disais, on avait un besoin très particulier et on avait testé ça : http://psom.simexp-lab.org/, mais ça ne te sera a priori d’aucune aide.

J’ai trouvé une immense liste d’outils qui font le genre de chose que tu cherches (on y retrouve AirFlow). Par contre, j’ai peur qu’avec que ce tu décris, ton besoin soit assez spécifique et nécessite de l’adaptation pour avoir vraiment ce que tu cherches.

Je plaide coupable pour les mots-clés peu informatifs, on trouve beaucoup plus de choses avec "processing pipeline".

Si tu as déjà ton graphe de calcul comme une structure de donnée en python, l’algorithme récursif dont je parlais est très simple à implémenter, c’est un parcours de graphe classique. On parle de 100 lignes de code max. Je ne suis pas sûr que tu aies besoin de chercher une bibliothèque spécialisée pour faire ça, à moins que tu aies des besoins poussés derrière en monitoring, etc. (Mais dans ce cas tu serais plutôt sur une exécution en direct des calculs et pas un pré-traitement.)

Une solution en OCaml:

type graph = rule list (* graphs as just lists of rules *)
and rule = { output: target; input: target list; }
and target = string

type problem = {
  graph: graph; (* the dependency graph *)
  up_to_date : target -> bool; (* which targets are already built *)
  required: target list; (* which targets we want to build *)
}

module TMap = Map.Make(String) (* sets of targets *)
module TSet = Set.Make(String) (* associative maps of targets *)

(* represent graphs as associative maps instead of lists *)
let graph_deps graph : target list TMap.t =
  List.to_seq graph
  |> Seq.map (fun {input; output} -> (output, input))
  |> TMap.of_seq

let need_to_build problem : TSet.t =
  let deps = graph_deps problem.graph in
  let not_needed target todo =
    problem.up_to_date target || TSet.mem target todo in
  let rec require target todo =
    if not_needed target todo then todo
    else TSet.add target (require_all (TMap.find target deps) todo)
  and require_all targets todo =
    List.fold_right require targets todo
  in
  require_all problem.required TSet.empty

Par exemple, on peut partir de l’exemple de départ:

let example =
  let im1, im2, im3 = "im1", "im2", "im3" in
  let r1, r2, r3 = "R1", "R2", "R3" in
  let rall = [r1; r2; r3] in
  let o1, o2, o3, o4, o5, o6 = "O1", "O2", "O3", "O4", "O5", "O6" in
  let c1, c2, c3 = "C1", "C2", "C3" in
  let m1, m2, m3 = "M1", "M2", "M3" in
  let graph =
    let mk output input = { output; input; } in
    [
      mk im1 [];
      mk im2 [];
      mk im3 [];

      mk r1 [im1];
      mk r2 [im2];
      mk r3 [im3];

      mk o1 rall;
      mk o2 rall;
      mk o3 rall;
      mk o4 rall;
      mk o5 rall;
      mk o6 rall;

      mk c1 [o1; o2];
      mk c2 [o3; o4];
      mk c3 [o5; o6];

      mk m1 [c1];
      mk m2 [c2];
      mk m3 [c3];
    ]
  in
  let up_to_date target =
    List.mem target [o1; o2; c2; m2; m3]
  in
  let required = [m1; m2; m3] in
  { graph; up_to_date; required }

et on a

# TSet.elements (need_to_build example);;
- : TSet.elt list = ["C1"; "M1"]

(Ici j’ai demandé seulement M1/M2/M3 comme produits finaux pour avoir une sortie plus courte, mais ça marche aussi si on demande C1/C2/C3 et M1/M2/M3 comme dans l’exemple de départ.)

Etant en train de réaliser cela dans un langage de glu, je ne cache pas que j’espérai trouver quelque chose de près à l’emploi. D’autant que le besoin me parait assez classique. Effectivement, ça s’implémente très bien, mais cela implique des tests supplémentaires, etc. Je profiterai de mon implémentation manuelle pour l’ajuster à d’autres petites spécificités incrémentales de ma situation exacte.

Pour le monotoring, cela viendra dans un second temps. Mon premier objectif était de simplifier/nettoyer le DAG des dépendances avant de confier le résultat à un framework qui me dispatchera les tâches correspondantes, typiquement Dask.

Merci pour la solution OCaml. Maintenant j’avoue que c’est un langage que je ne parle pas du tout ^^’. J’y jetterai un coup d’oeil à tête reposée.

En pseudo-code:

• tu maintiens un todo, un ensemble des cibles que tu as prévu de compiler
• si tu as besoin d’une cible, si elle est déjà buildée ou déjà dans le todo, tu n’as rien à faire
• sinon, tu l’ajoutes au todo, et tu visites toutes ses dépendances (tu en as besoin aussi)

Effectivement, ça s’implémente très bien, mais cela implique des tests supplémentaires, etc.

Oui enfin des tests il faut en faire aussi si on utilise une bibliothèque tierce. Et comme ce sont plutôt des tests d’intégration, ils peuvent être plus difficiles à bien faire.