Salut,
Voilà qui éclaircit pas mal de choses !
C’est une histoire de calcul des moments des force non?
En effet !
Je n’ai pas ce qu’il faut pour faire des dessins sous la main, donc je vais essayer avec juste du texte, si ce n’est pas assez clair j’essayerai de faire un schéma.
Ta question, c’est "à partir de quelle masse l’électro-aimant va lâcher".
Je commence par la découper en deux parties :
- Quelle est la force appliquée à l’électroaimant qui correspond à une masse posée sur la charnière ?
- Est-ce que cette force suffira à faire lâcher l’électroaimant ?
La deuxième question est assez triviale, et je vais donc me concentrer sur la première.
Tu l’as dit toi-même, c’est une question de moment.
Dans un système à l’équilibre, la somme des moments autour d’un axe est nulle :
i∑Mi=0
Ici, en se plaçant sur la pièce qui contient les bras, on a 3 moments :
- le moment créé par l’aimant Ma
- le moment créé par la masse posée sur la charnière Mc
- le moment de la réaction du sol sur les bras Ms
Un moment doit se calculer par rapport à un axe, et est nul lorsque la force à son origine est appliquée à cet axe. Donc, pour simplifier, je vais me placer à l’endroit où les bras touchent le sol.
Ce qui nous donne Ms=0, et donc :
Mc+Ma=0
Ici, nous sommes dans un cas particulier où toutes les forces sont appliquées dans la direction haut-bas, ce qui fait que les moments peuvent se calculer de cette manière :
Mi=Fidi ; avec Fi la force correspondant au moment Mi, et di la distance horizontale entre l’axe de calcul du moment et le point d’application de Fi.
On se retrouve alors avec :
Fcdc+Fada=0
Le jeu, maintenant, c’est de calculer da et dc.
dc est la longueur horizontale qui sépare le bout des bras de la charnière. Tu nous donne la longueur L de ce bras, et θ l’angle de ce bras à la verticale, ce qui avec un petit bout de trigo donne dc=Lsin(θ).
da est la longueur horizontale qui sépare le bout des bras de l’électroaimant. Tu nous donnes la longueur qui sépare la charnière de l’aimant (dac pour moi), on a donc : da=dac+dc, soit :
da=dac+Lsin(θ)
On remplace dans l’expression des moments :
FcLsin(θ)+Fa(dac+Lsin(θ))=0
Avant-dernière étape, on doit transformer la masse que tu poses en force (le poids) : Fc=mg
mgLsin(θ)+Fa(dac+Lsin(θ))=0
Expression finale
En retournant un peu l’expression :
Fa=−dac+Lsin(θ)mgLsin(θ)
Avec, je le rappelle :
- Fa la force exercée sur l’aimant
- m la masse posée sur la charnière
- g l’accélération gravitationnelle de la Terre
- L la longueur des bras
- θ l’angle des bras à la verticale
- dac la distance entre la charnière et l’aimant
On peut aussi voir la chose dans l’autre sens : à telle force (la force qui fait lâcher l’électroaimant), quelle masse.
m=−FagLsin(θ)dac+Lsin(θ)
(On retrouve ton intuition, qui est que si l’angle θ est nul, la masse peut être théoriquement infinie)
Comme je n’ai pas d’outil de calcul pratique pour faire celui-ci, je te laisse le soin de le faire, ça m’évitera de m’emmêler les pinceaux.
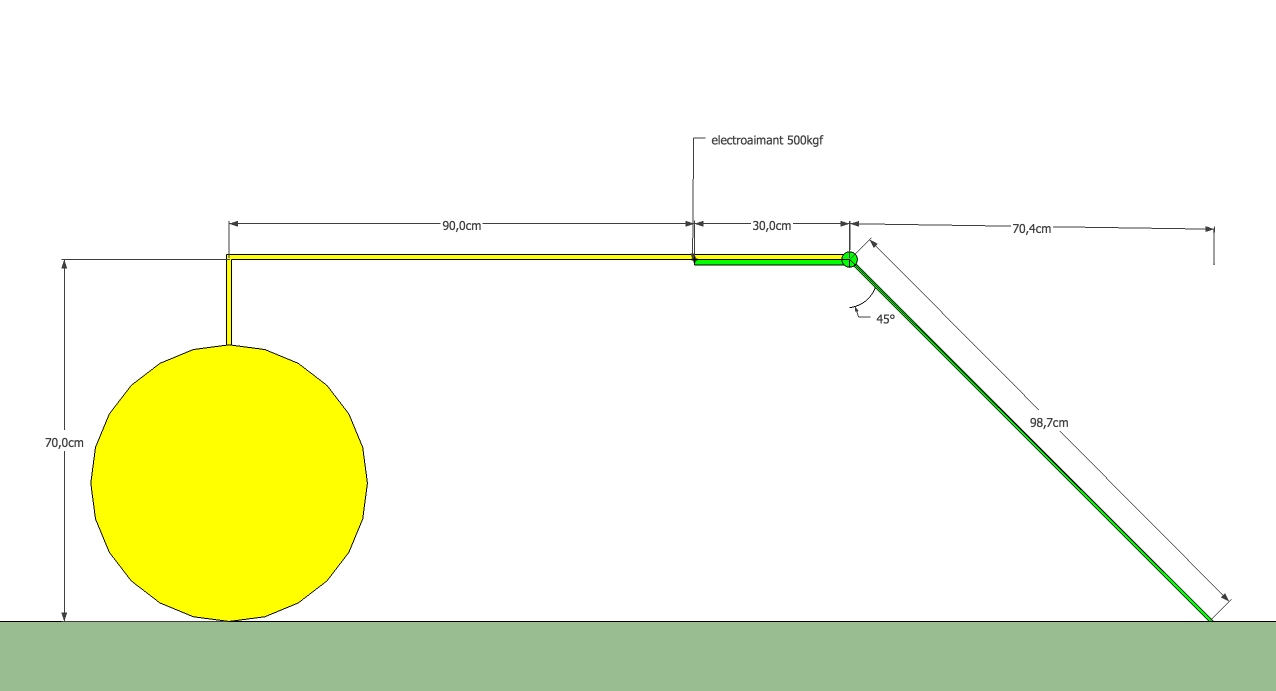
je suis en train de réaliser une charrette avec un mécanisme pour un spectacle de théâtre. je vous ai fait un petit schéma
|