Trigonaliser une matrice

Bonjour,

j’essaye de comprendre comment résoudre la question suivante :

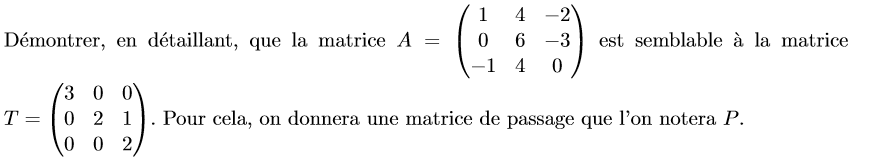
J’ai réussi à déterminer le polynôme caractéristique, et les sous-espaces propres de A. Les valeurs propres sont 3 (simple) et 2 (double). J’ai pu ainsi trouver la matrice de passage :

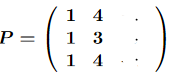
Mais je ne comprends pas comment trouver la dernière colonne, j’ai donc regardé un corrigé que je ne comprends pas non plus :

Je ne vois pas pourquoi w doit vérifier Aw = v + 2w. Je vois un lien avec Ker(A-2In) et le vecteur v (qui a un lien avec la valeur propre 2), mais je n’arrive pas vraiment à percevoir son origine.

Merci d’avance pour votre aide

Sources :

Enoncé sujet CCP 2011 MP MATHEMATIQUES 2

Corrigé de Omar SADIK

Ils sont tous deux disponibles sur ce site : https://concours-maths-cpge.fr/

Merci pour ta réponse, donc si la matrice T est de la forme : $\begin{pmatrix} 3 & 0 & 3 \\ 0 & 2 & 0 \\ 0 & 0 & 2\end{pmatrix}$

On chercherait un vecteur qui vérifie $A(w)= 2w + 3u$ ?

Ouip

Merci beaucoup