Former des identifiants pour retrouver des combinaisons d'index

Bonjour,

Sur un programme que je développe, j’ai le problème suivant :

Soit un ensemble de groupe d’éléments. Tous ces éléments sont numérotés de 1 à nb_element. Un groupe a au moins 1 élément et au plus max_element_per_group. Parmi ces groupes, je choisi soit un élément, soit aucun.

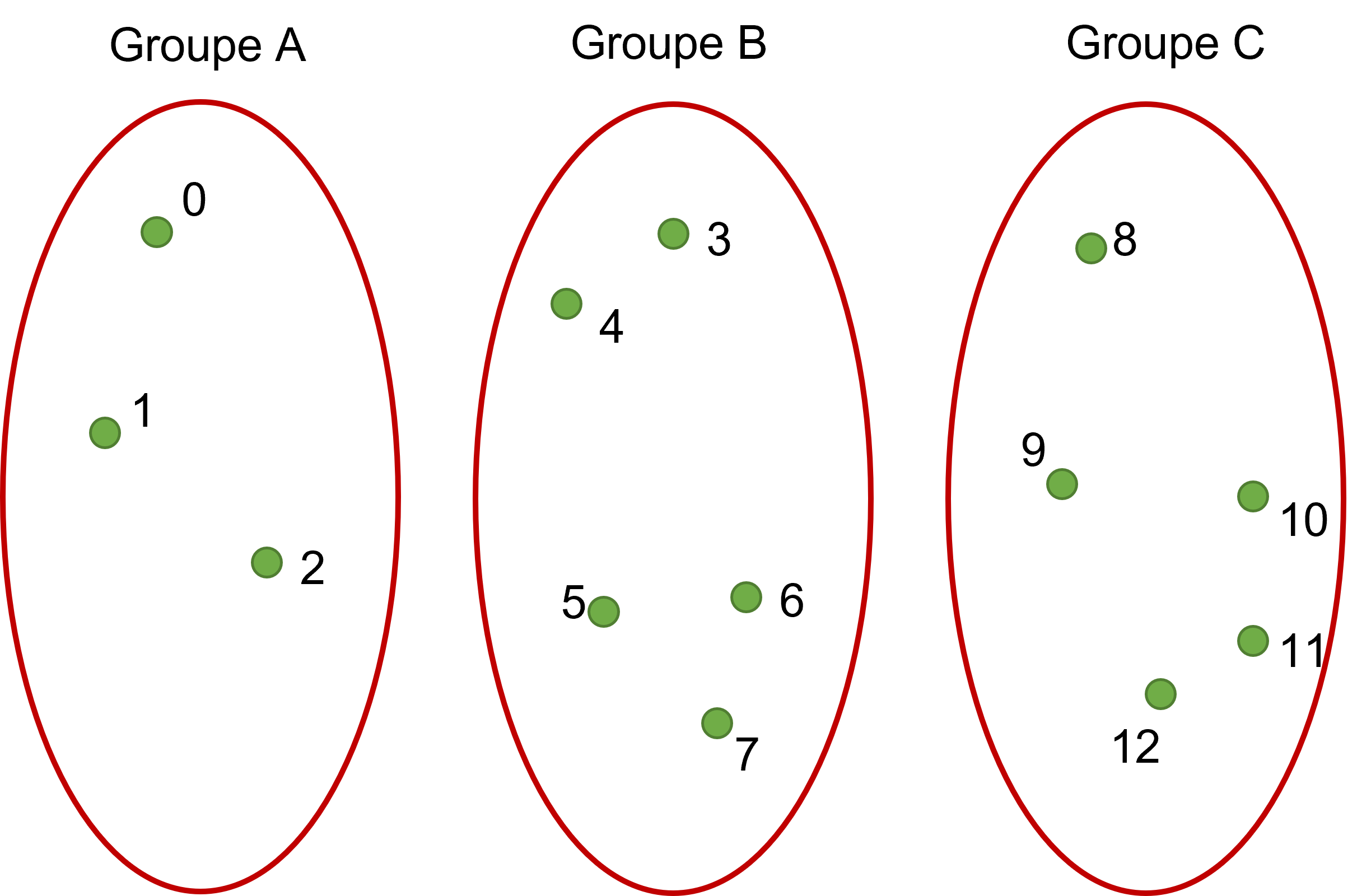
Par exemple sur le schéma précédent, j’ai 3 groupes, $A$, $B$ et $C$. Les éléments ont chacun un index, de telle sorte que nb_element = 13 et max_element_per_group = 5.

Maintenant je souhaite produire un identifiant unique (int32) pour indiquer les éléments que j’ai choisi parmi ces groupes. Par exemple dans le groupe $A$ j’ai choisi l’élément 1. Dans le groupe $B$ j’ai choisi aucun élément et dans le groupe $C$ j’ai choisi l’élément 9, mon identifiant serait par exemple 654895 (j’invente). Et à partir de ce nombre je saurai retrouver la sélection.

Ce problème vient du fait que je travaille sur GPU et qu’aujourd’hui je me retrouve à produire une liste d’index d’éléments. Mon programme serait beaucoup plus rapide si j’arrive à remplacer cette liste par un entier me permettant de recalculer cette liste d’index au besoin.

J’ai pensé à représenter ce problème sous forme matricielle, avec l’axe $x$ représentant les groupes et l’axe $y$ l’indice du plot dans le groupe (de 0 à max_element_per_group). J’ai ainsi une matrice de 1 et de 0. N’y a t-il pas un moyen, connaissant les dimensions de cette matrice, de l’exprimer avec un entier ?

Je sais bien qu’il est possible que ce problème n’ai pas de solutions… Mais bon, ça vaut le coup de demander.

Merci pour votre aide.

Salut,

Une matrice de 1 et de 0, c’est une liste d’entiers en écriture binaire, si jamais ça t’aide.

Hello,

C’est marrant, ton problème me fait un peu penser à KNN (même si ton problème n’est pas du tout cela).

Comme l’a dit Aabu, utilisait la représentation binaire pourrait être une solution.

Par contre, ce ne serait pas forcément du 32 bits, mais du $log_2(max\_element\_per\_group) * Ceil(nb\_element / max\_element\_per\_group)$.

Tu pourra ainsi split/shift la représentation binaire du nombre résultant par paquet de $log_2(max\_element\_per\_group)$ bits pour avoir l’index de chaque groupes.

Je ne sais pas si ça peut marcher, mais je sais qu’il existe un système qui fonctionne comme ceci :

• Element 1 : 1
• Element 2 : 2
• Element 3 : 5
• ….

Ainsi, si seulement l’élément 1 est sélectionné, tu as le résultat 1. Si les éléments 1 et 3 sont sélectionnés, tu as le résultat 1+5=6. Si les éléments 2 et 3 sont sélectionnés, tu as le résultat 2+5=7. Pour 1 et 2, tu obtient 1+2=3. Enfin, si tout les éléments sont sélectionnés, tu obtiens le résultat 1+2+5=8.

Je ne me souviens plus exactement comment ça marche, ni même comment ça s’appelle, mais je sais que ça permet, avec un entier, de retrouver une sélection.

Peut être que les autres agrumes pourront te donner plus de détails.

Edit : Mon exemple ici est mauvais, je suis pas certain de mes valeurs. Mais en gros, le but, c’est que chaque éléments ont une valeur qui ne peuvent pas être obtenus avec une addition d’autres valeurs.

Edit 2 : Pas sûr, mais il me semble que les valeurs sont tous simplement 1, 2, 4, 8, 16, … . Bref, plus trop de souvenir, donc je laisse les autres répondre.

L’idée de FougereBle, ce sont les tableaux de bits. Ça rejoint essentiellement l’idée d’écriture en binaire.

Ici tu as 3 groupes A B et C.

Mais on s’en moque totalement. Tu as 13 éléments, et la seule question, c’est de savoir quels éléments sont choisis parmi les 13. Les groupes A B et C ne nous servent à peu près à rien.

Comme dit par tous les autres, tu as besoin d’un tableau de 13 bits. (Rappel, un int32 est un tableau de 32 bits)

Si dans la vraie vie, tu as plus de 32 éléments, il n’y a pas de solution pour stocker toute cette information dans un int32.

Dans ce cas, tu regroupes les éléments par paquets de 32, et tu utilises un int32 pour chaque paquet de 32 éléments.

Si tu veux pouvoir stocker le max_element_per_group et que l’index garde un sens après que tu ajoutes un où des éléments, tu ne peux plus utiliser des étiquettes qui croissent entre les groupes. Ou alors comme dis @elegance, ça n’a plus d’importance d’utiliser les groupes alors.

Si on se base sur ce qu’a dit elegance, tu peux juste calculer ton index comme ça :

$1 * 2^1 + 1 * 2^9 = 514$

Où $1 * 2^n$ désigne que tu prends l’élément $n$.

Tu peux facilement retrouver les éléments choisis en faisant des divisions par 2.

Bonjour, merci pour vos réponses.

Oui j’avais pensé au tableau de bit mais 32 bits ne sont pas suffisant pour l’ensemble des éléments que j’ai à garder. Je pensais passer à côté d’une méthode mathématique qui m’aurait permis de résoudre mon problème mais oui, maintenant que vous en parlez, le tableau de bit est sûrement la méthode la plus efficace pour mon problème. Mais je me retrouve à faire un tableau de int si je veux pouvoir sauver l’ensemble de mes éléments malheureusement.

Merci encore !

Si tu as 300 éléments, il te faut 300/32 = 9.37 arrondi au dessus à 10 int32.

Il te faut donc un tableau de 10 INT32.

Mais je pense que dans beaucoup de langages, tu peux déclarer un tableau de 300 Bits à la place de ce tableau de 10 INT32. Et le système va bien gérer ça, à l’économie.

Pour toi, ce sera un peu plus simple, puisque les éléments seront numérotés de 0 à 299 ; c’est plus simple que si tu dois gérer des petits groupes de 32 (ce n’est pas non plus archi-compliqué)

Tu as à peu près combiens de groupe et combien d’éléments ?