Résolution d'un problème d'attribution de tache liés entre elles

alliocha1805, jeudi 13 octobre 2022 à 11h43
Modifié

Bonjour à tous,

Je me tourne vers le forum car je suis dans un impasse sur un challenge personnel que je me suis lancé niveau code.

Mon souci intervient bien avant le code mais dans la logique même de résolution du souci.

Le problème

J’ai une liste de tache qui doivent être résolu par une entité. Chaque tache possède une "valeur" et la charge qu’elle imposera (ou non) à chaque équipe de l’entité Je souhaiterai savoir s’il y a un moyen de calculer le sous ensemble de tache (automatiquement) qui serait le plus proche possible des contraintes suivantes :

Maximiser la valeur totale
Qu’aucune équipe n’est une charge qui dépasse 1.1 (les charges sont exprimées de 0 à 1)
Si une tache est prise alors toutes les équipes qui sont impactées doivent la prendre

Un exemple (très simplifié) de mes données source serait ceci (avec X la valeur et Yx les charges pour chaque equipe a/b/c/…) :

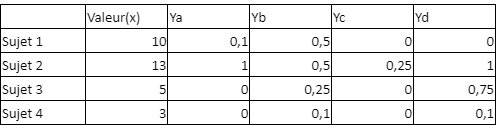
Après discussion avec diverses personnes on me donne tout un tas de réponse mais elles se contredisent ensemble sur la méthode la plus simple pour arriver à la solution du coup je suis un peu perdu

Merci à tous ceux qui pourront m’aider

13/10/22 à 11h43
Modifié

+0 -0

pierre_24, jeudi 13 octobre 2022 à 12h15
Modifié

Je suis pas spécialiste, mais j’ai deux tips:

On dirait une variante du problème du sac à dos (maximiser une valeur tout en ayant une limite sur une autre variable). J’ai l’impression que c’est une manière intéréssante d’attaquer le problème, et ça te donnera probablement des pistes pour l’algo.
… On est d’accord que dans l’absolu, répartir des tâches est un problème NP-complet, non ? (en tout cas, le problème du sac à dos l’est)

13/10/22 à 12h15
Modifié

#JeSuisToujoursArius • Docteur, mais en chimie ⚗️ • dev' quand il peut.

+2 -0

Aabu, jeudi 13 octobre 2022 à 12h16
Modifié

Salut,

Ton problème semble voisin de problèmes qui n’ont pas d’algorithmes exacts efficaces. Par exemple, ça ressemble à une variante du problème du sac à dos. Ces problèmes ont tendance à être NP-complets, donc durs en théorie, ce qui n’empêche pas d’avoir des algorithmes relativement efficaces en pratique. Mais n’attends pas de miracles ou de solution universelle.

Quoi qu’il en soit, il semble possible de formuler ton problème sous forme de problème d'optimisation en nombres entiers. Il existe alors plein d’outils plus ou moins efficaces en fonction des spécificités de ton problème (tant qu’il n’est pas démesurément grand). Tu pourrais aussi en programmer un si c’est ce qui te motive.

La modélisation ressemblerait à ça :

tu cherches une sélection de tâches $(t_1, ..., t_n)$ , où les $t_i$ sont soit 0 (la tâche est laissée de côté) soit 1 (la tâche est prise) ;
cette sélection doit maximiser la valeur totale, qui s’exprimera sous la forme $t_1 \cdot v_1 + ... + t_n \cdot v_n$ , où les $v_i$ sont les valeurs de chaque tâche ;
tout en respectant les contraintes de chaque équipe, qui seront de la forme $t_1 \cdot c_1^j + ... + t_n \cdot c_n^j <= 1.1$ , où les $c_i^j$ sont les charges pour la tâche i pour l’équipe j.

Ce genre de formulation est ce qui est compris par les bibliothèques et logiciels d’optimisation qui vont ensuite te donner un résultat.

Niveau outils déjà faits, je ne connais que des produits commerciaux et assez chers (Gurobi, CPLEX par exemple) qui semblent être interfacés avec Python, mais j’imagine qu’il y a aussi des bibliothèques en libre accès.

13/10/22 à 12h16
Modifié

+2 -0

Gil Cot, jeudi 13 octobre 2022 à 12h33

Quand j’ai lu :

Maximiser la valeur totale

J’ai tout de suite pensé : oh, un problème d’optimisation locale… et linéaire (on parlait de programmation linéaire pendant mes études, et après avoir énuméré divers algos, on étudiait surtout le simplexe…) ceci dit, je ne sais pas si ces considérations vont t’aider dans ta quête.

13/10/22 à 12h33

“It is seldom that liberty of any kind is lost all at once.” ― David Hume

+0 -0

etherpin, jeudi 13 octobre 2022 à 12h40

Je ne suis pas certain d’avoir bien compris le problème, car le vocabulaire est changeant. Je comprends que les "tâches" sont des "sujets" dans le tableau. Ensuite, je comprends que l’"entité" est constitué d’équipes.

Sur ces bases, je note que si une équipe a déjà une charge de 1 pour une tâche, , alors elle ne peut pas participer à une autre tâche avec une charge non nulle.

Dans ton tableau, la tâche 2 (valeur 13) exclu tout autre tâche, car la charge de l’équipe c ne lui permet pas de faire 3 ou 4, et la charge de a lui interdit 1.

13/10/22 à 12h40

Il se faut s’entraider, c’est la loi de la nature. (Jean de La Fontaine, l’âne et le chien)

+0 -0

gasche, jeudi 13 octobre 2022 à 12h46

Il y a des outils génériques pour résoudre ce genre de problèmes (des problèmes d’optimisation sous contraintes). Les détails de la situation (nombre entiers ou réels, optimisation ou juste satisfiabilité etc.) influent sur quelle famille d’outil sera la plus efficace, mais tant que le problème est raisonnablement simple (~ moins de 1000 inconnues à résoudre) n’importe quelle approche qui permet d’exprimer le problème va marcher.

J’essaierais avec Z3 par exemple, un solveur SMT qui supporte aussi les contraintes d’optimisation, ou Gecode, un outil standard pour la résolution de contraintes. Chercher un truc plus spécialisé, ou écrire du code soi-même, seulement si ces outils ne font pas le job.

13/10/22 à 12h46

+1 -0

Vlammar, jeudi 13 octobre 2022 à 12h48

C’est en effet le problème du sac à dos. Il existe des solutions plus performante que de naivement tester les solutions. Tu peux utiliser un solveur comme https://choco-solver.org/ ou http://minisat.se/ le premier utilise une modélisation CSP qui est plus simple à comprendre et utiliser. Sinon tu peux faire une modélisation SAT de ce problème et utiliser l’algo DPLL (ou minisat) https://fr.wikipedia.org/wiki/Algorithme_DPLL ce sera moins performant qu’un solveur mais ce sera toi qui implémentera tout. Si le temps est trop long tu as des améliorations comme l’algo MAC (maintaining arc consistency) http://www.constraint-programming.com/people/regin/papers/optmac.pdf

13/10/22 à 12h48

+1 -0

alliocha1805, jeudi 13 octobre 2022 à 14h56

Merci des réponses ca me fait beaucoup de lecture

Bon même si je sent que je me lance dans une croisade qui va largement dépasser mes connaissances mathématiques -___-

13/10/22 à 14h56

+0 -0

ache, jeudi 13 octobre 2022 à 21h41
Modifié

C’est bien un problème du Sac à dos multidimensionnel.

13/10/22 à 21h41
Modifié

ache.one 🦹 👾 🦊

+0 -0

gasche, jeudi 13 octobre 2022 à 23h39

Pour le fun j’ai écrit un encodage au format smtlib de ton problème de départ.

; Déclarations des valeurs du tableau, ligne par ligne
; V{i}: valeur, Y{team}{i}: charge
(define-fun V1 () Int 10)
(define-fun Ya1 () Real 0.1)
(define-fun Yb1 () Real 0.5)
(define-fun Yc1 () Real 0.)
(define-fun Yd1 () Real 0.)

(define-fun V2 () Int 13)
(define-fun Ya2 () Real 1.)
(define-fun Yb2 () Real 0.5)
(define-fun Yc2 () Real 0.25)
(define-fun Yd2 () Real 1.)

(define-fun V3 () Int 5)
(define-fun Ya3 () Real 0.)
(define-fun Yb3 () Real 0.25)
(define-fun Yc3 () Real 0.)
(define-fun Yd3 () Real 0.75)

(define-fun V4 () Int 3)
(define-fun Ya4 () Real 0.)
(define-fun Yb4 () Real 0.1)
(define-fun Yc4 () Real 0.)
(define-fun Yd4 () Real 0.1)


; C{i}: True si la tâche i est effectivement choisie, False sinon
(declare-const C1 Bool)
(declare-const C2 Bool)
(declare-const C3 Bool)
(declare-const C4 Bool)


; CSumInt, CSumReal: sommes pondérées
(define-fun CSumInt ((v1 Int) (v2 Int) (v3 Int) (v4 Int)) Int
  (+ (ite C1 v1 0) (ite C2 v2 0) (ite C3 v3 0) (ite C4 v4 0)))

(define-fun CSumReal ((v1 Real) (v2 Real) (v3 Real) (v4 Real)) Real
  (+ (ite C1 v1 0) (ite C2 v2 0) (ite C3 v3 0) (ite C4 v4 0)))


; Vtot : valeur totale des taches choisies
(define-const Vtot Int (CSumInt V1 V2 V3 V4))

; Y{team}tot: charge totale de l'equipe {team}
(define-const Yatot Real (CSumReal Ya1 Ya2 Ya3 Ya4))
(define-const Ybtot Real (CSumReal Yb1 Yb2 Yb3 Yb4))
(define-const Yctot Real (CSumReal Yc1 Yc2 Yc3 Yc4))
(define-const Ydtot Real (CSumReal Yd1 Yd2 Yd3 Yd4))

; les charges totales ne peuvent pas dépasser 1.1 (pourquoi pas 1.0 ?)
(assert (<= Yatot 1.1))
(assert (<= Ybtot 1.1))
(assert (<= Yctot 1.1))
(assert (<= Ydtot 1.1))

; on cherche à maximiser la valeur totale
(maximize Vtot)
(check-sat)
(get-value (C1 C2 C3 C4 Vtot Yatot Ybtot Yctot Ydtot))

Sur l’interface en ligne Z3 online demonstrator, je copie-colle ma source et je clique "Execute" et j’obtiens le résultat suivant:

(+ (ite C1 10 0) (ite C2 13 0) (ite C3 5 0) (ite C4 3 0)) |-> 26
sat
((C1 true)
 (C2 true)
 (C3 false)
 (C4 true)
 (Vtot 26)
 (Yatot (/ 11.0 10.0))
 (Ybtot (/ 11.0 10.0))
 (Yctot (/ 1.0 4.0))
 (Ydtot (/ 11.0 10.0)))

Traduction: il faut choisir de faire les tâches 1, 2 et 4 (mais pas 3), on obtient une valeur totale de 26 et les équipes a, b et d ont atteint la charge maximale de 1.1 (mais c est à 0.25).

Voilà. Je pense que c’est clair que tu peux "facilement" générer une description de problème de ce genre pour n’importe quelles données en entrée — ou appeler l’API Z3 pour construire le problème sans passer par sa représentation textuelle.