Diviseur de tension et courant dans une diode

Ou un truc qui doit m'échapper

Le problème exposé dans ce sujet a été résolu.

Bonjour,

En ce moment je cherche à me mettre à l’électronique, et je sèche sur un exercice qui aurait pourtant dû être tout simple. Tout d’abord, j’ai le montage suivant avec une diode quelconque :

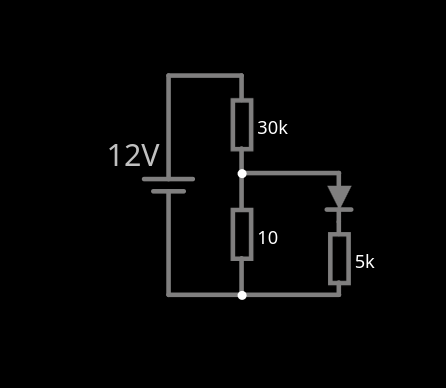
Soit les valeurs suivantes:

R1=30kΩR_1 = 30 k \Omega

R2=10ΩR_2 = 10 \Omega

R3=5kΩR_3 = 5 k \Omega

et la tension de la diode est je pense de 0,7 V. Le but est de changer la résistance R2 pour faire en sorte qu’il y ait un courant de 0,25 mA dans la diode.

J’ai utilisé plusieurs méthodes et j’avoue que j’ai fini par regarder la correction. Il se trouve que la résistance devrait faire 23 kOhm (comme en témoigne la simulation )

Lors de mes calculs, je n’ai jamais réussi à trouver ce résultat, et j’ai pourtant utilisé plusieurs techniques :

  • Circuit équivalent de Thévenin
  • Pont diviseur de tension et calcul de la tension à appliquer en entrée de la seconde "boucle" (aux bornes de R2).
  • Loi des nœuds, des mailles, etc.

Bref, parfois je retombe sur le même résultat que précédemment, mais jamais sur le résultat attendu. Peut-être qu’il y a quelque chose que je n’ai pas compris dans le fonctionnement de la diode…

J’ai essayé à la fin de calculer en faisant ID=Vs−VDRs=VR2−VDR3=0,25mAI_D = \frac{V_s - V_D}{R_s} = \frac{V_{R_2} - V_D}{R_3} = 0,25 mA

Et ensuite de calculer la valeur de R2 qu’il faudrait pour que le pont diviseur nous donne bien la valeur de VR2V_{R_2}, mais je n’ai toujours pas la bonne valeur… Je trouve environ 5.82 kOhm. Auriez-vous une idée de ce que j’aurais pu oublier de faire ?

Merci à vous ;)

+0 -0

Salut,

L’application (rigoureuse) de la loi des nœuds et des mailles est une méthode qui marche à tous les coups. Utiliser des circuits équivalents donnerait le même résultat, et serait adaptée ici, mais je n’ai pas essayé. Et surtout, on ne peut pas appliquer le diviseur de tension, car tout le courant qui traverse R1 ne traverse pas R2, puisque il y a du courant dans la deuxième branche.

Pour appliquer systématiquement les lois des mailles et des nœuds :

  1. Nomme toutes les grandeurs du circuit : les courants dans les branches, les tensions, etc. Identifier celles connues (R1, R3, le courant à travers la diode, …) et celles inconnues à ce stade.
  2. Écrire toutes les lois des mailles (ici, il y a deux mailles indépendantes).
  3. Écrire les lois des noeuds dans le circuit (une seule loi des noeuds non redondante dans ton exercice).
  4. Écrire les lois des composants (ici 3 lois d’Ohm, car il y a trois résistances et une pour la diode qui impose sa tension de seuil car elle est passante par hypothèse).
  5. Compter les grandeurs inconnues, compter les équations. Si tu as plus de grandeurs que d’équations, tu ne pourras pas fixer toutes les valeurs à des constantes. Sur mon brouillon, j’ai 5 équations et 5 inconnues, donc c’est bon.
  6. Utiliser les équations pour former l’expression de R2 (et potentiellement toutes les autres grandeurs).

Le point 6 est celui où il ne faut pas se tromper dans les calculs. J’ai fait les calculs tranquillement et je confirme que la valeur de R2 qui donne le résultat attendu est proche de 23 kΩ.

Je te conseille de bien poser tout ça sereinement et revenir si tu as des questions sur les calculs.

+3 -0

Salut,
Je viens insister un peu sur le pont diviseur de tension, parce que je trouve qu’on me l’avait mal présenté et c’est peut-être aussi ton cas. On avait fait tôt la démonstration du pont diviseur de tension car c’est une application simple de la loi des mailles. Seulement, on m’a ensuite pointé cette formule en la soulignant, en la nommant (pont diviseur de tension) et en me la faisant appliquer au travers d’innombrables exercices. À tel point que c’était un peu une formule magique à appliquer dès que je voyais ce schéma. Mais, on oublie ainsi très vite une hypothèse que l’on voit très bien dans la démonstration, que Aabu a rappelé : les résistances doivent être traversées par le même courant !
Enfin, en théorie … parce que ça n’a pas vraiment d’application pratique si on s’y tient strictement … mais comme on est physicien et pas mathématicien, on va dire qu’on peut appliquer cette formule quand le courant dans la branche dérivée est négligeable (généralement un rapport au moins 100, mais ça dépend aussi de la précision que tu as sur tes composants et ton circuit).
Le courant de la branche dérivée n’est pas du tout négligeable dans ton cas.
Si tu ne l’as pas déjà fait, je te conseille de refaire la démonstration de la formule du pont diviseur de tension pour te rendre compte de tout ça.
Et donc, je trouve qu’il ne faut pas vraiment retenir la formule du pont diviseur de tension, il s’agit juste d’un montage courant, pas d’une loi, elle n’est pas essentielle et peut nous induire en erreur.

Concernant ton exercice,
Si tu prends la grande maille, tu t’apercevras que tu n’as qu’une inconnue, le courant total. Tu pourras ensuite utiliser la loi de noeuds pour trouver le courant traversant R2. Avec l’une des deux petites mailles, tu pourras trouver la tension aux bornes de R2. Et maintenant que tu as ces 2 grandeurs, il ne reste qu’à calculer R2.

+0 -0

Merci @Aabu pour ta réponse,, j’étais effectivement parti sur autre-chose que la loi des nœuds, pensant qu’un diviseur de tension ou un circuit équivalent aurait été plus pertinent. Je savais pas qu’on ne pouvait pas utiliser le diviseur de tension dans ce cas-là…

J’ai donc suivi les étapes que tu as indiquées, et je tombe bien sur cinq équations et cinq inconnues (si on excepte la loi des nœuds qui fait une équation en plus, mais dont les inconnus sont déjà dans les autres). J’ai donc deux équations de loi des mailles que j’additionne pour annuler un terme. J’obtiens le courant I1 que j’ai pu injecter dans la première équation me permettant alors de retrouver R2.

Bref, merci beaucoup, je trouve bien 23 kΩ pour R2. Je me suis toutefois confronté à un problème, c’est que j’avais oublié que dans la loi des mailles les résistances de la deuxième n’avaient pas la tension dans le même sens :-°

@romantik, merci pour la précision, je pensais effectivement qu’on pouvait appliquer le pont diviseur à chaque fois qu’on avait un schéma avec deux résistances en série et qu’on voulait avoir la tension sur la deuxième. Comme tu m’as conseillé, je vais essayer de refaire la démonstration du pont diviseur de tension. Et aussi de courant, car j’imagine qu’il doit y avoir un problème analogue entre les deux.

+0 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte