Est-ce que tu parles du taux comme étant la mesure du débit à un instant donné ? (Qui correspondrait donc à l'ordonnée de ton graphe-signal)
Si c'est le cas, pour la moyenne, tu peux t'intéresser aux notions de moyennes mobiles, et là tu auras alors un signal lissé vers la moyenne (le lissage le plus puissant que tu peux faire étant de tout écraser sur la moyenne du signal), mais il va falloir que tu arrêtes de parler du "taux" quitte à paraphraser la notion que tu veux étudier avec des mots moins précis en l'illustrant avec des exemples.
Si tu as des notions de calcul infinitésimal/intégral, la notion de dérivée de fonction a pour "équivalent" dans les suites la différence $D(a_n)_n = a_{n+1}-a_n$ (où D est l'opérateur qui "dérive" la suite $(a_n)$, et donne donc une suite).
Tu peux le deviner en regardant les quotients $\frac{f(t+dt) - f(t)}{dt}$ par $\frac{f(t+1) - f(t)}{t+1-t} = f(t+1) - f(t)$, et d'ailleurs, $a_n$ est alors croissante ssi $D(a_n) >= 0$ pour tout $n$. Si tu as des variations dans ta suite, faire cette opération (et éventuellement la répéter) va donc les accentuer, et si tu as des termes qui ne varie peu, ils vont avoir tendance à disparaitre. En électronique, ça serait un filtre passe-haut (qui laisse passer les hautes fréquences).
La notion de moyenne au contraire, est plus liée à l'intégration : si tu définis l'opérateur $I$ par $I(a_n) = \sum_{i=n-N}^{n} a_i$, tu fais exactement une intégration (il faut imaginer le diagramme en bâton, tu intègres un premier bâton de largeur 1 et hauteur $a_{n-N}$, donc d'aire $1\cdot a_{n-N}$, puis tu fais pareil avec tous les bâtons, et en sommant tu as l'aire de tous les bâtons entre $a_{n-N}$ et $a_n$, donc c'est l'intégrale entre $a_{n-N}$ et $a_n$ de ton signal en bâton (en considérant qu'entre $t$ et $t+1$ ton signal ne varie quasiment pas).
Diviser ensuite par le nombre d'éléments sur lequel tu sommes, c'est une opération de "normalisation" ensuite. D'ailleurs la moyenne d'une fonction réelle continue est définie exactement de la même manière, mais avec une intégrale. Ici, c'est l'inverse, si tu as des composantes basses fréquences (presque constante) dans ton signal, elles vont avoir tendance à rester, et les hautes fréquences vont avoir tendance à partir.
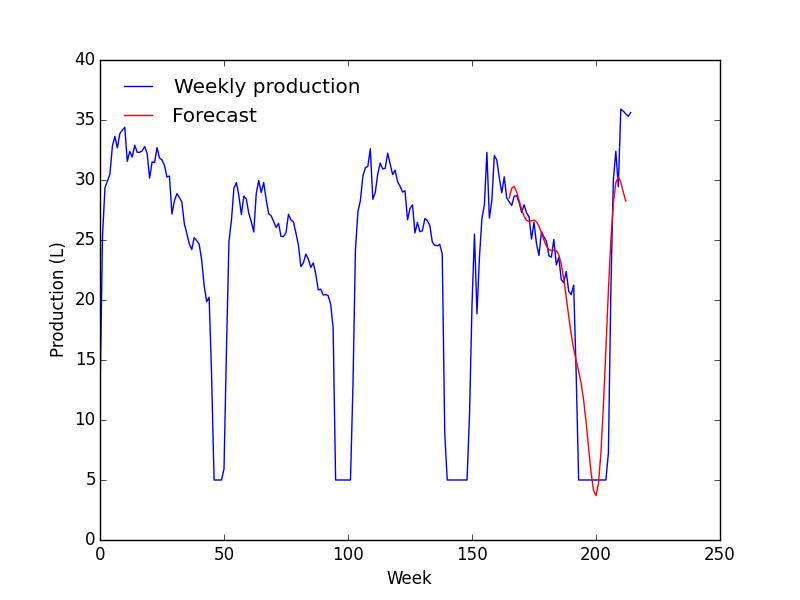
Par contre, ça, c'est pour du traitement "simple et naïf" de ton signal, éliminer du bruit ou avoir un ordre d'idée de comment évolue ton signal. Si tu souhaites prévoir comment ton signal évolue, il y a différentes techniques plus ou moins complexe, la plus "standard" étant de passer par une transformée de Fourier pour retrouver les-dites fréquences. Ca te permet en particulier de "constater" dans des cas simples que tu as une montée en charge tous les week-end par exemple.
Le défaut de ça, c'est que ça ne fonctionne "vraiment" que sur des signaux périodiques, sinon les fréquences que tu obtiens ne sont pas forcément révélateur, et prendre en compte tous ces paramètres d'évolution risque d'arriver très rapidement hors de ta portée (et parfois hors de la portée de n'importe quoi si tu n'as pas assez de paramètre pris en compte).
Mais tu dois vraiment comprendre quels opérations tu as besoin de faire sur ton signal, et à quelle quantité correspond ton signal traité, ou tu te retrouveras avec un signal qui a l'air d'être ce que tu veux mais qui ne représente pas du tout ce que tu cherchais à calculer, ou à mal interpréter ce que ton signal donne comme information.
L'utilisation d'une bibliothèque me paraît indispensable si tu n'as ni le bagage mathématiques, ni un signal bien régulier, ni même le temps.







 (je vais me débrouillé autrement, ca sera juste moins précis)
(je vais me débrouillé autrement, ca sera juste moins précis)