Pong
Le problème exposé dans ce sujet a été résolu.
Connectez-vous pour pouvoir poster un message.
Connexion
Connexion
Pas encore membre ?
Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte

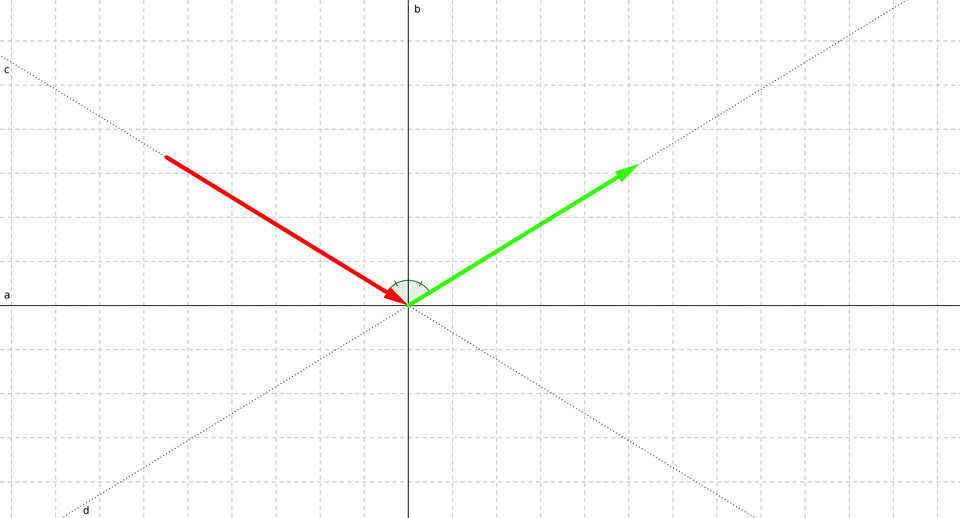

 mais tu peux aussi introduire un petit facteur qui simule la déformation de la balle sur la composante de la vitesse normale à la droite de collision
mais tu peux aussi introduire un petit facteur qui simule la déformation de la balle sur la composante de la vitesse normale à la droite de collision