Bonjour à tous,
J'aurais quelque questions à propos des interférences (niveau physique de Terminale S). On a appris cette formule pour calculer la différence de marche :
Déjà ici, trois questions :
- Qu'est ce qu'une différence de marche ? J'ai crû comprendre que c'était, en gros, la différence des trajets parcouru par les ondes.
- C'est quoi $k$ ?! Comment suis-je sensé trouver un coefficient ?
- Enfin, comment interpréter $\delta$ ? J'ai compris que si il était égal à $0$, alors l'interférence était constructive (la frange est brillante) mais autrement ?
Ensuite, on a fait un exercice aujourd'hui auquel je n'ai rien compris.
Deux fentes sont distantes de $a_{1-2} = 0,20mm$ et elles sont éclairées par un faisceau laser d'une longueur d'onde de $\lambda = 680nm$ On observe la figure d'interférence sur un écran placé à $D = 1,20m$ des fentes.
La première question était "La frange centrale est-elle brillante ou sombre ?". Nous avons trouvé brillante car $\lambda = 0$. On a simplement multiplié la différence de distance de trajet à la longueur d'onde. Serais-ce $k$ ? Ça m'étonnerais, il n'est pas sensé avoir d'unité (or une soustraction de distance à toujours une unité…).
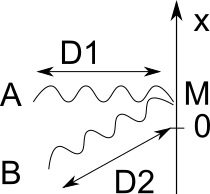
Enfin, on nous dit qu'en un point $M$ d'abscisse $x$, la différence de marche est donnée par la formule :
tranche sombre $\Rightarrow$ $\delta = (2k+1)\frac{\lambda}{2}$ (Bon ça d'accord, c'est mon cours, une interférence destructive, donc une frange sombre, ça se tient).
Comme on se trouve à la première frange, $k = 0$.
Donc :
Pour finir, $x = \frac{i}{2}$ je ne sais pas d'où ça sort…
Ça fait pas mal de questions, je sais ! Donc merci de votre lecture et de vos réponses !



 .
.

