Bonjour,
le simplexe est une méthode de résolution des problèmes d'optimisation linéaire.
Il a été introduit par " George Dantzig ". C'est probablement la premiere méthode permettant de minimiser ou maximiser une fonction sur un ensemble défini par des inégalités.
Les problèmes d'optimisation linéaire que la méthode du simplexe résout consistent à minimiser une fonction linéaire de n variables réelles, 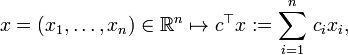
Le but est le suivant : prouver mathématiquement que s'il existe une solution et qui 'est optimale forcement est un point extrémal pour ce la y as des étapes a suivre .
Voila quelques rappelle on se met d'accord sur tous ceux si ,puis je pose l'étapes on pose la démonstation puis on passe a la suivante étape .

Passant aux étapes :

j'ai réaliser la question 1 et 2 , je suis bloquée au 3éme question (j'ai aucune idée )
voila ce que je propose comme solution pour question 1,2 :
1) Γ = { x∈ Rⁿ ;Ax≤b,x≥0 } Montrer que Γ est un ensemble convexe ! Soit x,y deux solution de Γ Ax ≤ b , x ≥ et Ay ≤ b , y ≥ 0 Ax - Ay + y ≤ b – b ⟺ Ax +(1- A)y ≤ b – b≤ 0 Soit z = Ax +(1- A)y (z est un point appartient au segment [x,y] ). Alor Az=b donc z ∈ Γ et z≥ 0. Donc Γ est un ensemble convexe.
2)
Montrer que Γ est un ensemble fermé!!
(il suffit de montrer que toute suit convergente de Γ converge vers un point de Γ)
Γ est un sous ensemble de Rⁿ
Soit une suite xn ∈ Γ, xn ≤ x , Axn ≤ Ax Axn ≤ b , xn ≥ 0 passage a la limite on aura Ax ≤ b , x ≥ 0 d’où x ∈ Γ , alors Γ est un ensemble fermé
Merci .

