Salut,
J'étais entrain de refaire des exercices et je n'arrive pas à résoudre un bête système d'équations.
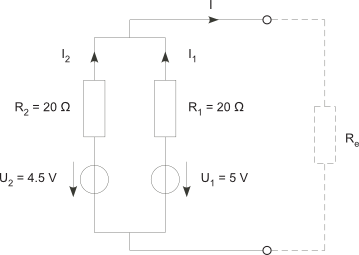
J'ai un circuit (le suivant) très simple, et je dois donner $I_1$ et $I_2$. Je trouve les équations de mailles et une équation de noeud, ce qui me donne trois équations linéairements indépendantes avec trois inconnues.
Cependant dès que j'isole $I_2$ ou $I$, je trouve respectivement du $I$ et du $I_2$ en plus de $I_1$…
Mais avec l'algorithme de Gauss, c'est extrèmement facile de résoudre ce système (ça me prends 2 secondes..) Cependant par une méthode normale, où j'isole et je substitue, je n'y arrive pas.
Voici mes équations de départ:
Quelqu'un a une astuce? Merci..
+0
-0




