Résistances

Le problème exposé dans ce sujet a été résolu.

Bonjour à tous,

J’essaye de calculer les résistances d’objets non-triviaux tel que cet anneau de résistivité $\rho$. Résistances d'anneaux

Dans le premier cas (image du dessus), le courant électrique se propage entre les surfaces $S_1$ et $S_2$.

Pour ce premier cas, je voulais prendre des surfaces "infinitésimales" $S = \pi L dR$. Comme dans chaque couche l’aire totale variera, l’intensité du courant n’est pas constante et donc les "résistances" sont en parallèle.

$$d[\frac{1}{R}] = \frac{{dS}}{{\rho \pi R}} = \frac{{\pi LdR}}{{\rho \pi R}} = \frac{{LdR}}{{\rho R}} \to \frac{1}{R} = \int\limits_{{R_1}}^{{R_2}} {\frac{{LdR}}{{\rho R}} = \frac{L}{\rho }\ln ({R_2}/{R_1})} $$

Deuxième cas (image du dessous), un courant électrique se propage entre la surface interne $S_1$ de rayon $R_1$ et celle externe $S_2$ de rayon $R_2$.

Ici, j’aurais pris la même surface mais pour moi elles sont toujours en parallèle car, comme avant, l’aire varie et donc le courant aussi (il diminue à chaque couche). $S = πrL$. Ce qui n’est pas possible il me semble. Le corrigé me dit que les résistances sont dans ce cas-ci en série et je vois pas pourquoi.

Merci d’avance!

+0 -0

Salut,

J’ai du mal à voir quels sont exactement tes éléments infinitésimaux.

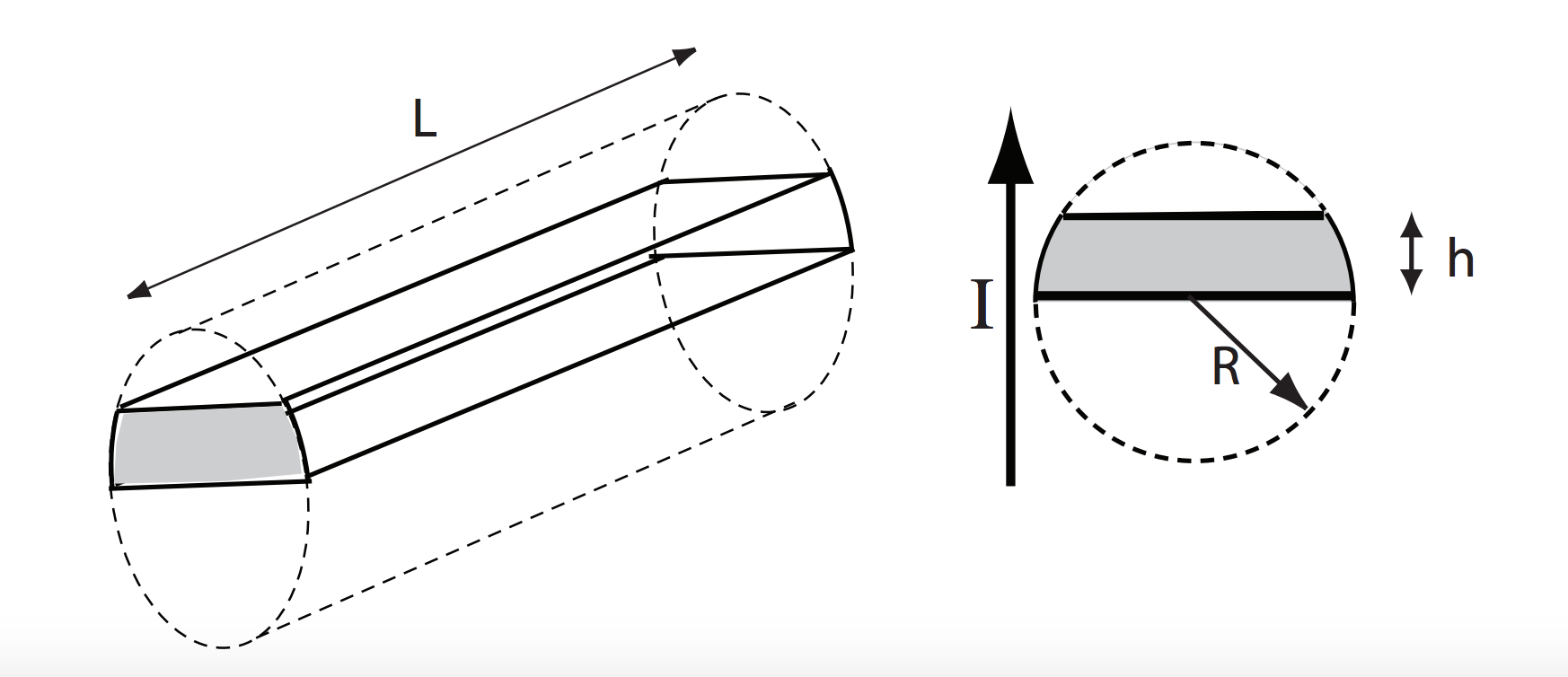
Si tu prends des couches concentriques, tu ne vas pas calculer la même résistance à chaque fois, même si la couche est identique. Dans les deux cas, tu peux te ramener à $R = \rho \frac{l}{S}$.

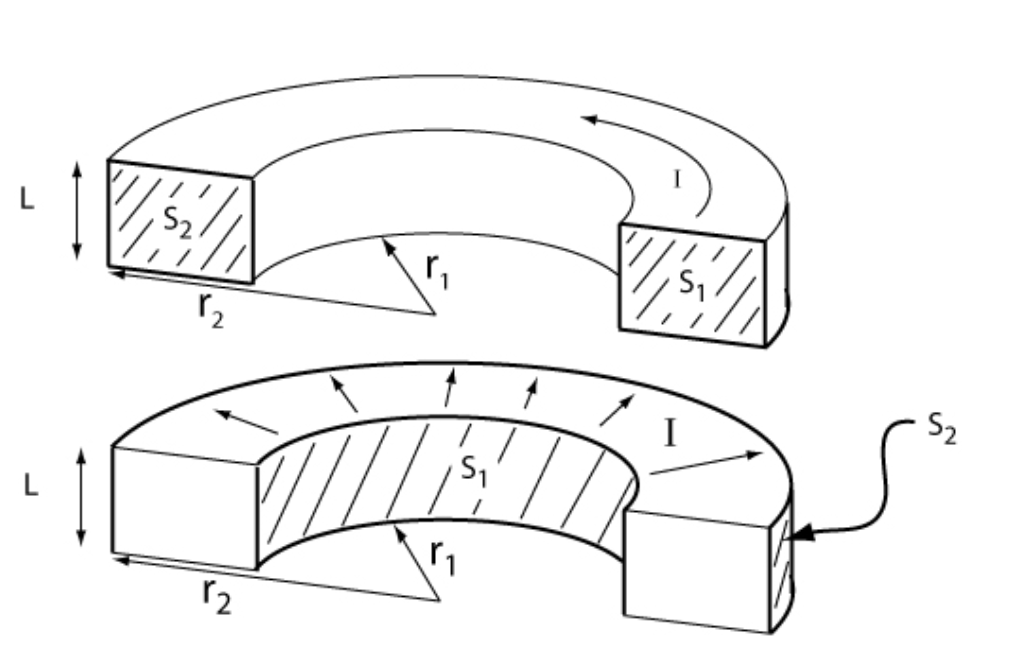
Dans le premier cas, $l$ correspond à la longueur de l’arc ($\pi r$), et la section $S$ est prise selon le rayon, perpendiculairement à l’arc (d’ailleurs, j’ai pas le même résultat que toi pour $\mathrm{d}S$, faudrait voir avec tes définitions de surfaces infinitésimales). On voit donc que les éléments sont bien en parallèle : à chaque face (noeud), la tension est la même, mais pas nécessairement le courant.

Par contre, dans le deuxième cas, $l$ correspond à l’épaisseur de l’arc ($\mathrm{d}r$), et la section $S$ est celle des faces de la couche concentriques (qui sont égales, puisque l’élément est infinitésimal, j’ai trouvé comme toi $\pi r L$). Ici, les éléments sont en série : le courant qui rentre par une face ressort par l’autre, qui est aussi la face d’entrée de l’élément suivant.

En fait, je crois que tu fais un raisonnement faux:

Comme dans chaque couche l’aire totale variera, l’intensité du courant n’est pas constante

Dans le premier cas l’aire présentée au courant ne change pas, mais la longueur oui. En s’éloignant du cœur, il y a plus de longueur, et donc plus de résistance par section infinitésimale. Tu l’as d’ailleurs écrit. Comme la tension est identique pour tous (ce qui définit la mise en parallèle !), on a bien le courant qui diminue dans chaque élement en s’éloignant du cœur.

comme avant, l’aire varie et donc le courant aussi (il diminue à chaque couche)

C’est faux ! Si le courant diminuait dans chaque couche, tu aurais I(S1) > I(S2)… Or, tu n’as pas de fuites. Le courant est bien conservé d’une couche à l’autre, mais pas la tension, qui va diminuer en s’éloignant du cœur.

+1 -0

Merci beaucoup Aabu. Vu comme ça, ça paraît effectivement évident et il faut donc raisonner sur le potentiel…

Pour voir si j’ai bien compris, j’essaye de trouver le résistance de la section d’un cylindre comme ici (h < R):

Résistance Cylindrique

Dans ce cas-ci j’imagine intégrer des petites couches d’épaisseur $dx$ de $0$ à $h$. Pour moi, toutes ces couches sont en série car le courant circule perpendiculairement et donc les potentiels sont différents (s’il circulait dans l’autre sens ça serait en $//$). J’ai du mal par contre à visualiser quelle est ma surface $S$. Je dirais $S = L \times l(x)$ mais je vois pas quoi prendre en $l(x)$. En gros, je me ramenerais à $R = \int\limits_0^h {\frac{{\rho dx}}{{Ll(x)}}} $

+0 -0

Salut,

Effectivement, tu peux procéder en faisant des couches infinitésimales empilées de 0 à h (donc selon $x$ dans tes définitions). Dans ce cas, ta section sera la section de matériau qui est perpendiculaire à $x$, comme tu l’as écrit, ce sera bien $S = L \times l(x)$, avec $l(x)$ qui est la largeur de la bande.

Nous ce qu’on veut, c’est $l(x)$. C’est facile de trouver ça si tu connais la distance $y(x)$ entre le bord du cercle et l’axe de symétrie vertical du cercle, parce que $l(x) = 2 y(x)$. Il suffit donc de pouvoir exprimer la distance d’un point du cercle par rapport à l’axe vertical (l’axe des $x$ chez nous), ça correspond aux coordonnées du points selon l’axe horizontal $y(x)$.

Comme on connaît l’équation cartésienne d’un cercle centré en zéro et de rayon $R$,

$$ x^2+y^2 = R^2, $$

on peut exrimer $y$ en fonction de $x$:

$$ y(x) = \sqrt{R^2-x^2}.$$

On en déduit :

$$ l(x) = 2\sqrt{R^2-x^2}.$$

Ensuite tu peux normalement t’amuser à intégrer ton expression.

+1 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte