Simulation de la position du Soleil

Salut ,

Je voudrais avec Three.js reproduire le résultat dispo sur ce site c’est à dire reproduire la position du soleil sur une sphere. Je n’ai aucun problème sur la création en elle même du cycle jour/nuit, je peux d’ailleurs vous montrer un apperçu:

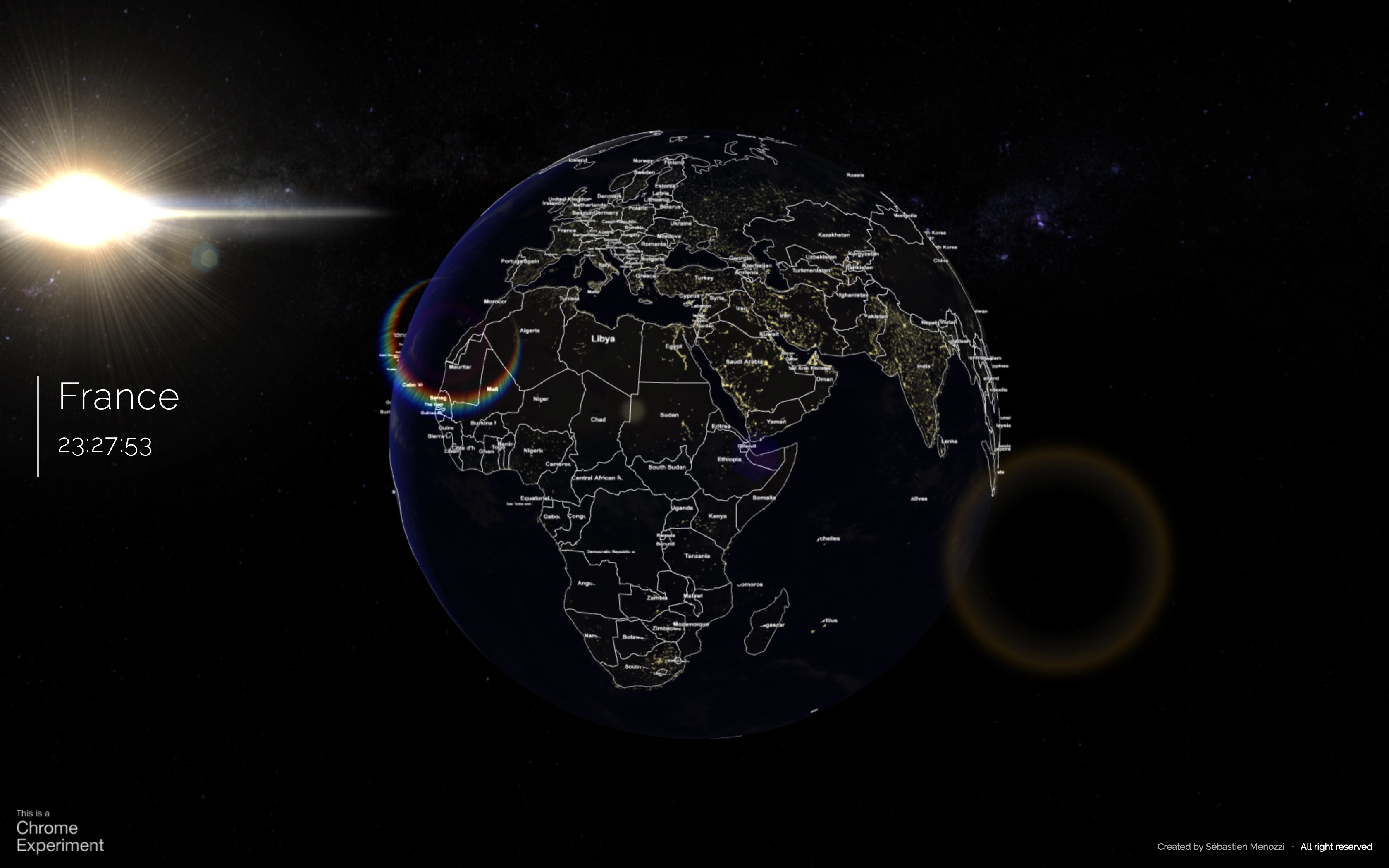
En fait, le projecteur de lumière se caractérise simplement ainsi:

1
2
3

var sun = new THREE.DirectionalLight(0xffffff, 1);
  sun.position.set(-600, 0, 1500);
  scene.add(sun);

Comme on peut le voir, la position du soleil est fixe et suit un vecteur ne réprésentant pas la "réalité". J’ai trouvé un projet correspondant exactement à ce que je veux faire et j’en ai extrait un code pour l’appliquer sur mon globe:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

function toRadians(degrees) {
    return degrees / 180 * Math.PI
  }
  function getJulianFromUnix(time) {
    return ((time / 1000) / 86400.0) + 2440587.5
  }

  function sunCoordinates(time) {
    let D = getJulianFromUnix(time) - 2451545
    let g = 357.529 + 0.98560028 * D
    let L = 280.459 + 0.98564736 * D

    let lambda = L +
      1.915 * Math.sin(toRadians(g)) +
      0.020 * Math.sin(toRadians(2 * g))

    let e = 23.439 - 0.00000036 * D
    let y = Math.cos(toRadians(e)) * Math.sin(toRadians(lambda))
    let x = Math.cos(toRadians(lambda))

    let rightAscension = Math.atan2(y, x)
    let declination = Math.asin(
      Math.sin(toRadians(e)) * Math.sin(toRadians(lambda))
    )

    let gmst = 18.697374558 + 24.06570982441908 * D
    let hourAngle = (gmst / 24 * Math.PI * 2) - rightAscension

    return {
      hourAngle: hourAngle,
      declination: declination
    }
  }

  var calculatedMoment = function() {
    return moment(new Date()).utcOffset(0)
  }

  var sun = sunCoordinates(parseInt(calculatedMoment().format('x')));

Il m’affiche comme prévu:

1

{ declination: -0.01716732820784288, hourAngle: 39605.66185791371 }

Mais comment réussir dans le cadre de mon projecteur à utiliser ces données pour reproduire la position du soleil ?

Merci

Tu as essayé de tourner la terre et ta caméra, au lieu de tourner le soleil ?

En effet, c’est une autre façon de procéder . Le problème est que mon globe est composé de plusieurs meshes. Il faut donc que j’effectue une rotation pour chacun, c’est pas très pratique, notamment en ce qui concerne le mesh s’occupant du cycle nuit où j’effectue justement des rotations…

Avec ThreeJS, on peut regrouper des objets comme un seul être.

Merci beaucoup, cela m’a beaucoup aidé dans la compréhension du phénomène. J’ai transformé le code de ta fonction a312() pour qu’il fonctionne dans un espace en 3 dimensions avec mon code:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

//FONCTIONS D'APRES LE PROJET GITHUB...

// On ajoute le projecteur de lumière
var dirLight = new THREE.DirectionalLight(0xffffff, 1);
  scene.add(dirLight);
var min = 0;

function day_night(time) {
  const coord = sunCoordinates(time.utcOffset(0).format('x'));
  const earthRadius = 200;

  const r = 1500;
  const h = coord.hourAngle;
  const d = coord.declination;
  let x = earthRadius + r * Math.cos(h)
  let y = 0
  let z = earthRadius + r * Math.sin(h)

  dirLight.position.set(x, y, z);
  dirLight.updateMatrix();
}

setInterval(function() {
  min++;
  let date = moment(new Date()).add(min, 'minutes');
  day_night(date);
}, 100);

On peut ainsi remarquer que l’axe y devient en 3D l’axe z (je t’apprend rien). Le résultat est bien celui espéré. Cependant j’ai un petit problème avec la deuxième fonction a312_2(), on remarque que c’est l’axe x et l’axe y qui varient, ainsi je suppose qu’il faille faire une sorte de mixe des 2 fonctions en ce qui concerne l’axe x et qu’il faille appliquer l’axe y de ta deuxième fonction à l’axe y, soit: let y = earthRadius + r * Math.sin(d-Math.PI)…

Pour A312_2 j’ai un peu tricher en utilisant cette méthode (j’ai utilisé un raccourci valable dans un monde 2D). Il faudra peut-être se baser sur le commentaire de mon premier message.

Dans un espace 3D j’ai peur que ça fasse : ( o ( au lieu de ( o ). C’est-a-dire qu’il faut tourner l’arc de cercle. Dans l’idée je pense qu’il faut ajouter un système de vecteur et remplacer mon -Math.Pi dans la fonction cos/sin (que j’ai mis pour avoir ( o et non ) o).

Pour joindre A312 et A312_2, il me semble, qu’il faut prendre en compte la valeur relative/constante une seule fois, c’est-à-dire enlever (230 ou 70) de la deuxième fonction et l’ajouter à la suite du premier calcul.