Le noyau atomique

On sait aujourd’hui qu’un atome est constitué d’électrons, légers, chargés négativement, orbitant autour d’un noyau, lourd, chargé positivement. Avant de parler plus avant de radioactivité, détaillons donc les constituants et propriétés du noyau.

L'atome

Les atomes sont composés d’un noyau entouré d’un cortège d’électrons. Le noyau est lui-même composé de neutrons, des particules non chargées, et de protons, chargés positivement. Tandis qu’un électron a une masse de 10-31 kg environ, celle d’un neutron ou d’un proton est nettement plus importante, environ 10-27 kg. Comme le nombre de protons et de neutrons dans un atome est similaire au nombre d’électrons, presque toute la masse de l’atome est concentrée dans le noyau. L’atome est essentiellement constitué de vide.

Il s’agit du modèle atomique de Rutherford1.

Travailler avec des masses de l’ordre de 10-30 kg n’est pas très pratique (un électron et un proton ont une masse ridiculement petite, même si elle est en vérité très différente), c’est pourquoi on utilisera deux autres unités.

La première se fonde sur l’équivalence masse-énergie, donnée par la formule E=mc2E=mc^2, avec E l’énergie de masse, m la masse et c la vitesse de la lumière dans le vide. Ainsi, on donnera les masses en électron-volt par c2 (eV/c2) et ses multiples2.
Un électron a une masse d’environ 500 keV/c2 et un proton ou neutron d’environ 900 MeV/c2.

La seconde est l'unité de masse atomique, qui vaut le douzième de la masse d’un atome de carbone 12 (soit 6 neutrons et 6 protons), à savoir 1,66.10-27 kg (soit 900 MeV/c2 environ). L’unité de masse atomique est notée u.

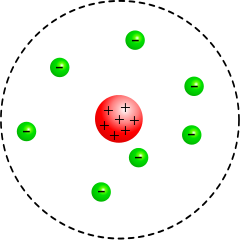
Modèle atomique d'après Rutherford -- Image libre de droits de Night Ink
Modèle atomique d’après Rutherford. Image libre de droits de Night Ink

Bien que les propriétés qui nous intéressent soient les propriétés nucléaires (c’est-à-dire liées au noyau), il est utile de garder quelques ordres de grandeur en tête concernant l’électron : sa masse est de 9.10-31 kg, soit 500 keV/c2, et sa charge de -1,6.10-19 C. Cette charge est la charge élémentaire ; toutes les particules ont une charge multiple de celle-ci3 (0, 1e, 2e, -1e…).

De la même manière, quelques ordres de grandeur concernant l’atome : les masse et rayon des atomes varient selon l’espèce chimique. Prenons le cas du carbone, qui est un atome de taille moyenne ; il fait environ 100 pm (picomètre, soit 10-12 m), de l’ordre de 2.10-27 kg, soit 900 MeV/c2, et est électriquement neutre.

L’expérience de Rutherford

En 1920, les collaborateurs de Rutherford envoyèrent un faisceau de particules censées être électriquement neutres (des particules d’hélium) sur une feuille d’or extrêmement fine. Les expérimentateurs visualisaient les particules envoyées par le faisceau sur un écran situé derrière, afin de voir comment celles-ci étaient déviées par les atomes de la feuille d’or.

Les particules du faisceau, sans charge électrique, ne devaient pas interagir avec les atomes de la feuille d’or (eux aussi neutres). C’était bien le cas pour 99,99 % des particules envoyées, mais 0,01 % des particules étaient déviées. La mesure des angles de déviation donnait des résultats assez variés, tous les angles semblaient possibles : certaines particules étaient même renvoyées en arrière.

Le moyen le plus simple pour expliquer le résultat était de postuler que l’atome est essentiellement vide, la quasi-totalité de la charge étant localisée au centre de l’atome. Ainsi, un atome est donc composé d’un noyau atomique entouré d’électrons. Les particules du faisceau déviées sont entrées en collision avec le noyau et ont rebondis sur le noyau. Une fois formulée mathématiquement, cette théorie prédit bien la déviation observée des particules du faisceau dans l’expérience de Rutherford.

Nuage électronique

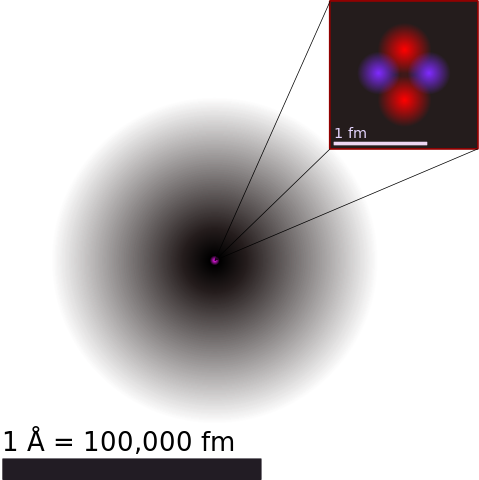
De nos jours, la mécanique quantique donne une image un peu différente de l’atome. Il y a toujours un noyau entouré d’un cortège d’électrons, mais les électrons ne sont plus localisés précisément dans l’espace. On s’intéresse alors à la probabilité qu’un électron soit présent en un certain point autour du noyau.

Image de Yzmo, wikicommons, GFDL et CC-BY-SA 3.0
Probabilité de présence d’un électron autour d’un atome d’hélium. Image de Yzmo, CC-BY-SA 3.0

  1. Assez simpliste, mais suffisant pour ce qui nous concerne — la radioactivité.

    ↩

  2. Un électron-volt est l’énergie cinétique acquise par un électron accéléré depuis le repos par une différence de potentiel d’un volt, soit environ 1,6.10-19 J.

    ↩

  3. Stricto sensu, les quarks ont une charge valant un multiple de e3\frac{e}{3}, mais ce ne sont pas des particules que l’on observe isolément. Ils sont toujours en groupe de tel sorte que la particule résultante a bien une charge multiple de e.

    ↩

Les constituants du noyau atomique

Les noyaux sont composés de particules plus simples, appelées nucléons1 (à savoir les protons et les neutrons). Ces nucléons possèdent, comme toutes les particules, les propriétés suivantes (qui peuvent valoir zéro) :

  • une masse ;
  • une charge électrique ;
  • une taille (encore mal connue) ;
  • une durée de vie ;
  • etc.
Spin et grandeurs conservées

Les particules possèdent d’autres grandeurs moins usuelles, comme le spin ou la couleur. Ces grandeurs sont intéressantes, car elles sont conservées lors d’une transformation. C’est-à-dire que si deux particules de spin SA et SB réagissent entre elles, alors les particules résultantes de spins individuels S1, S2, …, Sn devront respecter la condition ∑i=1nSi=SA+SB\sum_{i=1}^n S_i = S_A + S_B.

Concrètement, cela permet entre autre de détecter une particule instable. En partant des grandeurs qui se conservent des particules résultant de la désintégration, on peut en déduire les propriétés de la particule originelle.

Les particules du noyau : les nucléons

On illustre souvent le noyau sous la forme d’une framboise compacte, où les protons sont en rose et les neutrons sont en bleu. Nous conserverons cette convention.

Image de Marekich, wikicommons, CC-BY-SA 3.0
Exemple de noyau atomique. Image de Marekich, CC-BY-SA 3.0

Le proton

Le proton est un nucléon de masse 938 MeV/c2 (1,673.10-27 kg ou 1,007 u), soit près de 2000 fois plus que l’électron. Le proton est chargé électriquement ; sa charge est positive, de même valeur absolue que celle de l’électron. Sa taille est encore mal connue : certaines mesures donnent la valeur de 0,84 femtomètre2 alors que les mesures basées sur des collisions avec des électrons donnent une valeur proche de 0,88 fm.

Le neutron

Le neutron est aussi un nucléon, avec une masse très proche de celle du proton, 940 MeV/c2 (1,675.10-27 kg ou 1,009 u), soit 1,0014 fois plus. Sa charge électrique est nulle. Sa taille est similaire à celle du proton.

Histoire, un mot sur Prout

Dès le 19e siècle, certains scientifiques émirent l’idée que le noyau est composé lui-même de particules plus simples. Le premier scientifique à émettre cette hypothèse fût un médecin anglais nommé William Prout, en 1815. Celui-ci remarqua que la masse d’un atome était approximativement égale à un multiple de la masse du noyau d’hydrogène. Cette observation était autrefois nommée la règle de Prout.

L’hypothèse de Prout n’arrivait cependant pas à expliquer la charge électrique du noyau. Le noyau de l’hydrogène a une charge de e, égale à l’opposée de celle de l’électron. L’atome étant neutre, il doit donc y avoir autant de protons que d’électrons. Mais si on compare le nombre de protons calculé à partir de la masse et celui calculé à partir de la charge, on n’obtient pas le même résultat. Prenons par exemple l’atome de carbone 12 : vu que celui-ci contient 6 électrons, il devrait contenir 6 protons. Mais si on divise la masse d’un atome de carbone par la masse d’un proton, on obtient approximativement 12. Et ce problème se rencontre pour tous les noyaux excepté l’hydrogène 1H.

Les physiciens ont longtemps postulé la présence d’électrons dans le noyau, mais cette théorie des électrons nucléaires souffrait de nombreux problèmes techniques et expliquait mal certaines données expérimentales. Les physiciens se sont alors peu à peu rangés à l’idée que le noyau contient, en plus des protons, des particules qui ont une charge électrique nulle et une masse semblable à celle du proton. Cette particule a été découverte en 1932 par Chadwick, qui lui donna le nom de neutron. Par la suite, diverses observations sur les noyaux montrèrent que le neutron est bien parti prenante du noyau de l’atome.

Lorsque deux nucléons sont très proches, il apparait entre eux une force qui tend à les tenir ensemble (d’où la formation in fine de noyau). Ce phénomène est comparable, dans les grandes lignes, à la formation d’un atome à partir de noyaux et d’électrons. Dans le cas de l’atome, c’est l’interaction électromagnétique qui fait qu’électrons et noyaux s’attirent au point de s’assembler en atomes. Pour la formation d’un noyau à partir de nucléons, c’est l’interaction nucléaire : deux corps suffisamment proches (environ 3 femtomètres) se bloquent à une certaine distance fixe (environ 1 femtomètre), au point de s’assembler en noyaux dans le cas des nucléons. Même si, comme vous allez le voir, les choses sont un peu plus compliquées.

Interaction nucléaire et interaction forte

Commençons par un petit rappel sur les forces fondamentales. Elles sont au nombre de quatre :

  • la gravitation, force attractive exercée par tout objet massif ;
  • l’interaction électromagnétique, force exercée par tout objet chargé sur un autre ; c’est cette force qui tient ensemble électrons et noyau ;
  • l’interaction faible, une force assez complexe que je ne détaillerai pas tout de suite ;
  • l’interaction forte, force exercée entre deux objets possédant une couleur (la propriété couleur, absolument rien à voir avec les couleurs que nous percevons) ; c’est elle qui permet aux nucléons de rester stables.

Qu’en est-il du noyau ? Constitué de protons tous positifs et de neutrons, l’interaction électromagnétique tend à le disloquer. Les masses en jeu sont trop faibles pour que la gravitation fasse quoi que ce soit. L’interaction faible jouera un rôle dans leur désintégration, mais elle est trop faible pour permettre leur cohésion. L’interaction forte n’agit que sur les particules colorées et les neutrons et protons ne sont pas colorés (blanc ou neutre). Mais alors ?

La solution est un peu plus compliquée : la cohésion du noyau est un effet indirect de l’interaction forte. Pour comprendre, faisons une analogie avec l’interaction électromagnétique. Si je place une charge négative proche d’un atome, il ne va pas être attiré (il est neutre). Cependant, le nuage électronique de l’atome va lui être un peu perturbé. Ce faisant, l’atome n’est plus neutre (les champs créés par les électrons et les protons ne s’annulent plus parfaitement, puisque celui des électrons est décalé), une petite charge apparait sur l’atome. Une force s’exerce donc sur lui. C’est ce qui donne les dipôles induits et le phénomène de polarisabilité.

De la même manière qu’une charge peut affecter un atome neutre, à cause des phénomènes internes à celui-ci, l’interaction forte interne aux nucléons provoque une interaction, dite nucléaire, entre nucléons, alors que ceux-ci sont blancs.

Inutile de dire que l’interaction nucléaire est compliquée à décrire précisément. Son comportement est aujourd’hui connu, mais elle garde des mystères, comme savoir si elle dérive ou non d’un potentiel, par exemple.

Interaction nucléaire

L’expérience montre que l’interaction nucléaire peut être aussi bien attractive que répulsive : tout dépend de la distance entre les deux nucléons. Quand les deux nucléons sont extrêmement proches, l’interaction nucléaire est fortement répulsive. En conséquence, le noyau atomique est presque incompressible : rapprocher deux nucléons demande une force énorme pour compenser l’interaction nucléaire. Si les deux particules sont suffisamment éloignées (mais suffisamment peu pour que la force ne soit pas négligeable), l’interaction nucléaire est attractive. Tout cela peut se résumer avec le graphique suivant, qui montre la valeur de la force entre deux nucléons, exprimée en fonction de la distance qui les sépare.

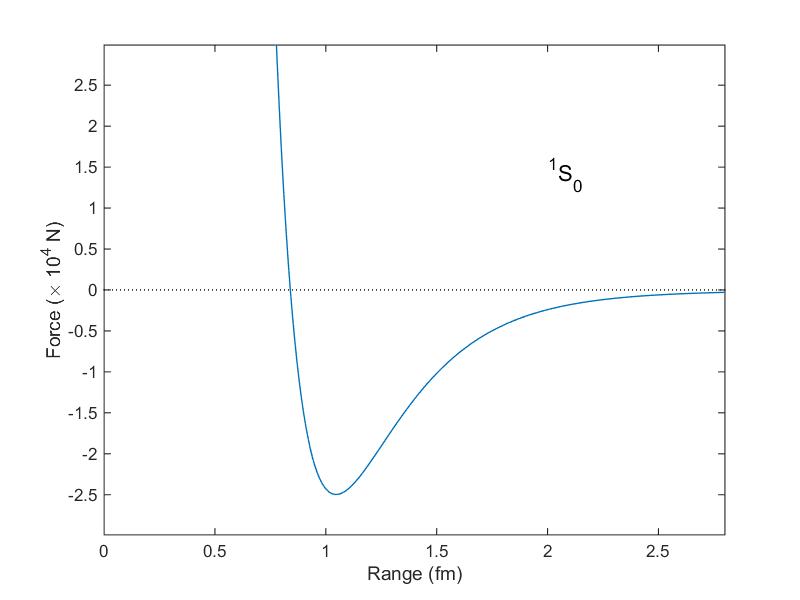
L'interaction nucléaire -- Image de Bdushaw, CC-BY-SA 4.0
L’interaction nucléaire — Image de Bdushaw, CC-BY-SA 4.0

Expérimentalement, cette force se moque de la nature des nucléons : à distance égale, cette force sera identique entre deux neutrons, deux protons, ou entre un proton et un neutron. Cette propriété est appelée l'indépendance à la charge.

Il est intéressant de remarquer qu’au delà de 1 fm, l’interaction nucléaire diminue rapidement avec la distance, plus vite que la répulsion électromagnétique entre protons. À partir d’une certaine distance, la répulsion entre protons sera plus forte que l’interaction nucléaire. Ainsi, les noyaux avec un grand nombre de protons auront tendance à se briser ou perdre des nucléons3, ils sont moins stables.

Potentiel nucléaire

La force nucléaire a des points communs assez forts avec la gravité, le magnétisme et l’électricité. Notamment, ces forces proviennent chacune d’une source : objet massif pour la gravité, charge électrique pour l’électricité, aimant pour le magnétisme, et nucléon pour la force nucléaire.

Avec la force nucléaire, chaque nucléon influence les nucléons environnants en leur fournissant une énergie potentielle nucléaire, qui dépend entre autre de la distance avec la source. La force nucléaire vient du fait que les nucléons tentent de minimiser leur énergie potentielle et se déplacent vers l’endroit où elle est la plus faible, c’est à dire proche du nucléon à l’origine du potentiel.

Cette énergie potentielle est impossible à calculer à l’heure actuelle (début 2016), même si diverses théories en donnent une approximation convenable. Historiquement, le premier modèle du potentiel nucléaire créé par un nucléon a été inventé par Yukawa en 1935. Selon sa théorie, le nucléon source émet des particules qui servent d’intermédiaires pour la force nucléaire. Quand un nucléon environnant absorbe ces particules intermédiaires, il est attiré ou repoussé du nucléon source. En élaborant cette idée dans le cadre de la physique quantique, Yukawa trouva la formule suivante pour le potentiel, où :

  • g est une constante ;
  • m est la masse de la particule intermédiaire ;
  • r est la distance entre les deux nucléons.

V=−g24πe−mrrV = - \frac{g^2}{4 \pi} \frac{e^{- m r}}{r}

  1. Vous remarquerez que ce terme partage la même racine que les mots « nucléaires » et « nucléation », et quelques autres : ces mots partagent la même racine latine nucleus, qui signifie noyau.

    ↩

  2. Un millionième de milliardième de mètre, soit 10-15 mètres.

    ↩

  3. Même si d’autres paramètres rentrent en ligne de compte et peuvent stabiliser le noyau, comme un bon nombre de neutron. Nous verrons ce qu’est un bon nombre dans la prochaine partie.

    ↩

Les propriétés du noyau atomique

Évidemment, tous les noyaux ne se ressemblent pas : le noyau de l’atome d’hydrogène n’est pas celui du béryllium, par exemple. Les différences entre noyaux peuvent porter sur des choses assez diverses : nombre de nucléons, nombre de protons, nombre de neutrons, charge électrique, taille, forme, etc. Et il se trouve que toutes ces propriétés sont reliées entre elles, la plupart dépendant du nombre de protons et de neutrons.

Nombre de nucléons

Un noyau contient un nombre bien précis de nucléons, ce nombre étant appelé le nombre de masse : celui-ci est noté A. Ce nombre de masse est la somme du nombre de protons Z et du nombre de neutrons N.

A=Z+NA = Z + N

Deux atomes ayant le même nombre de protons et de neutrons se comportent de la même manière.

Espèce chimique et isotopes

Si deux noyaux ont le même nombre de protons, ils appartiennent à la même espèce chimique (les atomes de carbone ont 6 protons, ceux d’uranium 92, par exemple).

Si deux noyaux ont un même nombre de protons, mais pas le même nombre de neutrons (et donc pas le même nombre de masse), ce sont des isotopes. Ainsi, l’hydrogène a 3 isotopes : ceux-ci ont toujours un seul proton, mais le nombre de neutrons varie ; l’hydrogène1 n’a pas de neutrons, le deutérium a un neutron, le tritium a deux neutrons et il existe quelques autres isotopes de l’hydrogène avec plus de 3 neutrons. Citons aussi l’exemple des isotopes de l’uranium avec leurs 92 protons : l’uranium 238 contient 238 nucléons, l’uranium 235 en a 235, tandis que l’uranium 234 en a évidemment 234.

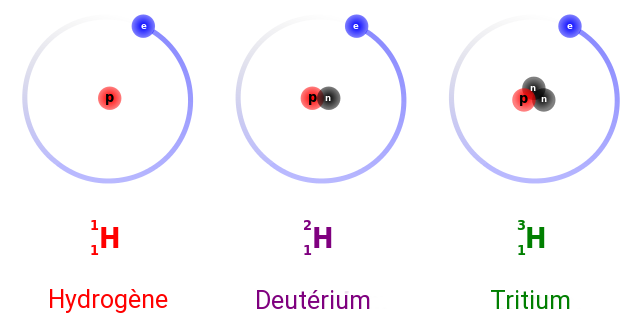
Isotopes de l'hydrogène, d'après Dirk Hünniger, CC-BY-SA 3.0
Isotopes de l’hydrogène, d’après Dirk Hünniger, CC-BY-SA 3.0.

Vu que les isotopes ont le même nombre de protons, ils ont aussi le même nombre d’électrons et donc des propriétés chimiques très similaires ; les atomes isotopes ont le même nombre de protons et donc la même place dans le tableau périodique, ils correspondent à un même élément chimique.

Isobares

Si des noyaux ont le même nombre de nucléons, mais pas le même nombre de protons ou de neutrons, ce sont alors des isobares. Par exemple, un noyau avec un nombre de masse égal à 3 peut contenir soit 3 protons, soit 2 protons et 1 neutron, soit 1 proton et 2 neutrons, soit 3 neutrons.

Vu que le proton et le neutron ont presque la même masse, on peut considérer que des isobares ont des masses identiques (en première approximation). A contrario, des noyaux qui ne sont pas isobares auront des masses sensiblement différentes.

Forme du noyau

La plupart des noyaux atomiques ont une forme sphérique, même si certains noyaux sont déformés et ont une forme ellipsoïdale assez marquée, voire plus bizarre encore. On constate expérimentalement que les noyaux aux formes bizarres sont des noyaux instables (qui se brisent rapidement en noyaux plus petits ou qui perdent fréquemment des nucléons). Par contre, les noyaux stables, qui survivent suffisamment longtemps pour qu’on puisse les étudier, ont une forme quasiment sphérique.

Dans ce qui va suivre, nous allons surtout travailler sur les noyaux sphériques.

Volume

Le volume du noyau dépend lui aussi du nombre de masse. En effet, les nucléons d’un noyau ont sensiblement la même taille et sont tous sphériques. De plus, le noyau est compact : tous les nucléons sont aussi proches les uns des autres que possible et l’empilement optimise l’espace utilisé. Le volume du noyau est donc proportionnel au nombre de nucléons.

On notera dans ce qui suit V le volume du noyau, Vn le volume d’un nucléon, rn le rayon des nucléons et r le rayon du noyau.

On a alors

V∝A×Vn=A×43πrn3V \propto A \times V_{n} = A \times \frac{4}{3} \pi r_n^{3}

Rayon nucléaire

De là, on calcule le rayon du noyau à partir de la formule qui donne le volume d’une sphère.

V=43πr3V = \frac{4}{3} \pi r^{3} A×43πrn3∝43πr3A \times \frac{4}{3} \pi r_n^{3} \propto \frac{4}{3} \pi r^{3} r3∝A×rn3r^{3} \propto A \times r_n^{3} r∝A3×rnr \propto \sqrt[3]{A} \times r_n

Le rayon d’un nucléon est approximativement égal à 1,4 femtomètres. Le noyau est donc extrêmement petit. Le rayon d’un noyau est 10 000 fois plus petit que celui de l’atome : il ne vaut que 0,01 % du rayon total de l’atome.

Densité

Une fois que l’on a calculé le volume du noyau, il est facile de calculer sa densité. Et chose étonnante, les expériences montrent que tous les noyaux ont la même densité. De plus, la densité est constante à l’intérieur du noyau. Il n’y a qu’en périphérie que la densité chute pour arriver rapidement à zéro, la diminution ayant lieu sur une partie bien précise du rayon. Expérimentalement, on observe que la portion où la densité chute a une épaisseur de quelques femtomètres, 2 à 3 tout au plus.

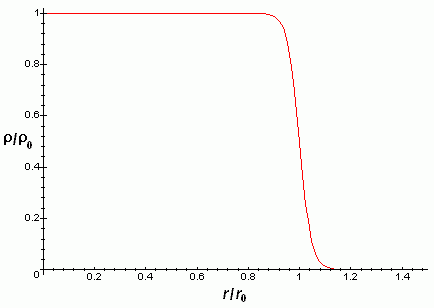
Densité d'un noyau sphérique par Davius, image libre de droits, wikicommons
Densité d'un noyau sphérique par Davius, image libre de droits, wikicommons

Le fait que la densité soit constante dans le noyau et qu’elle soit la même pour tous les atomes vient du fait que l’interaction forte soit à courte portée : elle sature au-delà d’une certaine distance. Ainsi, chaque nucléon n’interagit qu’avec ses voisins immédiats et pas avec ceux à l’autre bout du noyau. Si ces forces étaient sensibles à forte distance, on aurait une concentration des nucléons vers le centre (comme la concentration de particules dans un champ de gravité).

On peut calculer une approximation de la densité du noyau assez facilement, sous quelques hypothèses. Premièrement, nous allons considérer que le proton et le neutron ont la même masse m. Deuxièmement, nous allons supposer que la masse du noyau est égale à la somme des masses des nucléons : Mnoyau=A×mM_{noyau} = A \times m. Troisièmement, la densité ρ\rho est constante dans tout le noyau : on ne prend pas en compte la surface du noyau où la densité baisse. On a alors, en utilisant les équations de calcul du volume vues plus haut,

ρ=AmV∝A×mA×43πrn3\rho = \frac{A m}{V} \propto \frac{A \times m}{A \times \frac{4}{3} \pi r_n^{3}}

ρ∝3×m4πrn3\rho \propto \frac{3 \times m}{4 \pi r_n^{3}}

On retrouve le résultat qui veut que la densité soit indépendante du nombre de nucléons. Reste que cette estimation est relativement lâche, vu qu’elle ne prend pas en compte la pellicule extérieure où la densité baisse.

Allons plus loin

Pour cela, les physiciens calculent la densité à partir de la formule de Saxon-Woods, où :

  • ρ\rho est la densité ;
  • ρ0\rho_0 est la densité au centre du noyau (calculée avec la formule précédente) ;
  • r est la distance par rapport au centre du noyau ;
  • R est le rayon du noyau, dans la partie où la densité est constante ;
  • a est la longueur sur laquelle la densité chute rapidement en périphérie.

ρ=ρ01+exp⁡r−Ra\rho = \frac{\rho_0}{1 + \exp { \frac{r - R}{a}}}

Énergie et masse

Maintenant, il est temps de voir comment calculer la masse d’un noyau. Comme on l’a dit plus haut, un neutron a presque la même masse qu’un proton, si bien que la masse d’un noyau est approximativement égale au nombre de nucléons multiplié par la masse d’un proton, d’un neutron, ou bien de l’unité de masse atomique. En posant m la masse du noyau et ma l’unité de masse atomique, on a alors :

m=maAm = m_a A

Cependant, on peut être plus précis en tenant en compte la différence de masse entre un proton et un neutron. Dans ce cas, la masse du noyau est égale à la somme de la masse des protons et de celle des neutrons. En posant mp la masse d’un proton et mn la masse d’un neutron, on a alors :

m=Zmp+Nmnm = Z m_p + N m_n

Mais si on mesure expérimentalement la masse d’un noyau, on obtient un résultat légèrement différent de la masse calculée par la formule du dessus. Pour les noyaux stables, la masse mesurée du noyau est systématiquement plus faible que la valeur théorique. La différence entre la somme des masses des nucléons et la masse réellement mesurée est appelée le déficit de masse, noté Δm\Delta m.

m=Zmp+Nmn−Δmm = Z m_p + N m_n - \Delta m

Expliquons ce déficit de masse. On sait grâce à Einstein que la masse est une forme d’énergie comme une autre : l'énergie de masse. On peut calculer cette énergie de masse avec la fameuse formule E=Mc2E = M c^2, où E est l’énergie de masse, M la masse et c la vitesse de la lumière. Tout porte à croire que la masse manquante est transformée en une énergie provenant de l’interaction nucléaire ; cette énergie tient les nucléons liés dans le noyau, c’est l'énergie de liaison.

L’énergie de liaison est donc la différence d’énergie entre l’énergie de nucléons individuels et l’énergie de ces mêmes nucléons assemblés en noyau. Dit autrement, l’énergie de liaison est l’énergie qu’il faut fournir au noyau pour en séparer les nucléons. De même, on peut considérer que l’énergie de liaison est l’énergie libérée quand on rassemble plusieurs nucléons dans un noyau.

Cette énergie de liaison est négative : plus l’énergie de liaison est grande en valeur absolue (donc très négative), plus l’énergie du noyau sera inférieure à la somme de l’énergie des nucléons séparés (et plus l’atome sera stable).

  1. Le terme hydrogène signifie habituellement, selon le contexte, élément hydrogène (atome à un proton, quel que soit le nombre de neutron) ou atome à un proton sans neutron, contrairement à ses deux autres isotopes.

    ↩

Ainsi donc voilà l’atome et en particulier le noyau décrits. Composé de nucléons de deux types, le noyau est un amas de particule stabilisé par l’interaction nucléaire. Cette force inter-nucléons est reliée à une énergie de liaison. Cette énergie est reliée à une différence de masse entre les nucléons pris ensemble ou séparément.

Si cette énergie de liaison est insuffisante, l’atome peut être altéré. Ce sont les phénomènes de radioactivité, dont nous allons maintenant parler.

Sources

Il est compliqué de trouver des sources lisibles et scientifiques pour ce genre de contenu. Pour des sources lisibles, n’importe quel livre de physique de niveau bac devrait faire l’affaire. Pour les sources scientifiques, en voici quelques unes.