Vous êtes vous déjà demandé ce qu’est un son ? Comment évolue-t-il ? Quel est sa nature ? Pourquoi entendons nous de l’écho dans une pièce vide ? Quand un objet ou une personne émet un son, une onde de pression est émise : l’onde sonore. Dans ce tuto nous allons étudier l’onde sonore dans quelques situations classiques : sa propagation, la mesure du son et le phénomène d’écho. Il s’agit ici d’une introduction est nous ne traiterons pas de sujet avancés.
Les prérequis mathématiques sont faibles et la seule notion nécessaire est celle du logarithme en base 10. Si vous ne connaissez pas cette fonction, un bref rappel est fait dans le tutoriel. Un niveau bac scientifique est recommandé.
Dans un premier temps nous verrons les bases des sondes sonores, puis la mesure et la quantification des sons et enfin nous nous intéresserons de plus près à la réverbération sonore.
Ce tuto fait partie d’un CdS sur le son, je vous conseille vivement les autres publications. 
L'onde sonore
L’onde sonore
Pour bien comprendre en détails le comportement du son il est important de détailler sa nature ondulaire. En effet tout son est en fait une onde longitudinale de pression, c’est-à-dire une onde dont la perturbation est parallèle au déplacement. On l’appelle onde sonore.

Cette onde est caractérisée par sa fréquence et son amplitude. La fréquence correspond au nombre de fois où l’onde oscille pendant une seconde, elle est exprimée en Hertz (Hz). La fréquence correspond d’un point de vue auditif à la hauteur de la note. À une basse fréquence correspond un son grave et à une haute fréquence un son aigu.
L’amplitude de l’onde nous permet de savoir si le son est fort ou non. En acoustique on s’intéresse généralement à la puissance de l’onde qui est liée à son amplitude. Nous verrons comment quantifier et mesurer cette puissance un peu plus loin.
Une manière très simple de représenter une onde d’un point de vue mathématique en un point donné de l’espace est la suivante :
Voici quelques informations sur ces variables :
- $A$ correspond à l’amplitude de notre onde sonore. Plus l’amplitude est grande plus la puissance est grande : on entendra donc le son à un volume plus élevé (« plus fort »).
- $\omega$ est appelé pulsation de l’onde. Avec $ \omega = \frac {2\pi}T $ on voit apparaître la période $ T $ de notre onde. La période correspond à la durée d’une pulsation complète et est exprimée en secondes ($s$), c’est l’inverse de la fréquence.
- La variable $\phi$ est la phase de l’onde, c’est une variable qui permet de représenter le décalage possible entre deux ondes.
- Ce sont toutes les trois des réels positifs. La phase $\phi$ peut être parfois négative, mais on s’arrange par convention pour que ça ne soit pas le cas.
Cette manière de représenter est très utile pour comprendre les phénomènes acoustiques. En associant un phénomène acoustique (un son qui produit une onde sonore) à une équation il est facile de mettre en évidence de manière formelle des observations réalisées sur le terrain. Par exemple il existe des cas spécifiques où des ondes sonores peuvent s’annuler (partiellement ou totalement). En posant les équations, ces phénomènes acoustiques sont facilement explicables.
Ici nous avons travaillé avec un son pur, c’est-à-dire un son présentant une seule fréquence. Un son parfait en quelques sorte. Dans la nature les sons purs n’existe pas, ils sont constitués de plusieurs ondes à des fréquences différentes qui s’additionnent les unes aux autres. Même si l’on prend le cas simple d’une corde de guitare qui vibre, celle-ci ne produit pas un son pur (contenant une seule fréquence) mais un son riche. Ce dernier contient une fréquence fondamentale ainsi que des harmoniques. Les harmoniques sont des ondes dont la fréquence est un multiple entier de la fréquence fondamentale. Ainsi un son dont la fréquence fondamentale est de 440Hz, présentera des harmoniques à 880Hz, 1320Hz, etc.

Un vrai son est beaucoup plus complexe à modéliser et on se contente donc de notre cosinus dans la plupart des cas. En effet pour modéliser parfaitement une onde il faudrait prendre en compte sa fréquence fondamentale et ses harmoniques. Pour de nombreux phénomènes acoustiques on utilise le modèle simplifié d’un cosinus à la fréquence fondamentale. Le résultat obtenu pour la majorité des cas est tout de même valide. Il est possible de travailler avec un modèle plus complet en faisant appel à des outils de calculs ou à des simulations informatiques.
On peut aussi noter l’importance du milieu dans lequel l’onde se propage. Dans la plupart des cas on étudie l’onde sonore dans l’air, mais elle se propage dans n’importe quel milieu non vide. L’onde fonctionne par phase de compression et de dilatation, phénomène clairement visible sur l’illustration précédente. Plus la densité du milieu est importante, plus la vitesse de l’onde est grande. En effet plus la masse volumique et la compressibilité du milieu sont petites, plus la vitesse de propagation est grande. Ainsi dans l’air, la vitesse du son se trouve environ à $340 m \cdot s^{-1}$, alors que dans béton elle est de $3100 m \cdot s^{-1}$. Le calcul de la vitesse devient assez complexe dans les milieux mixtes comme par exemple de l’eau en présence de bulles d’air.

Une onde sonore ne se propage pas du tout dans le vide, n’ayant pas de milieu support à sa propagation. D’autres facteurs comme la température ou le taux d’humidité de l’air influent aussi sur la propagation sonore. Rien n’empêche à un milieu d’être solide, on parle alors de transmission solidienne de l’onde acoustique et non plus de transmission aérienne. Ce cas est beaucoup étudié en acoustique des bâtiments.
Qu’entend notre oreille ?
Pour mieux comprendre comment nous entendons, regardons de plus près le fonctionnement de notre oreille. Il s’agit ici d’un aperçu très rapide car le fonctionnement de notre système auditif mériterais un article à lui seul  . Voici une coupe schématique d’une oreille humaine :
. Voici une coupe schématique d’une oreille humaine :
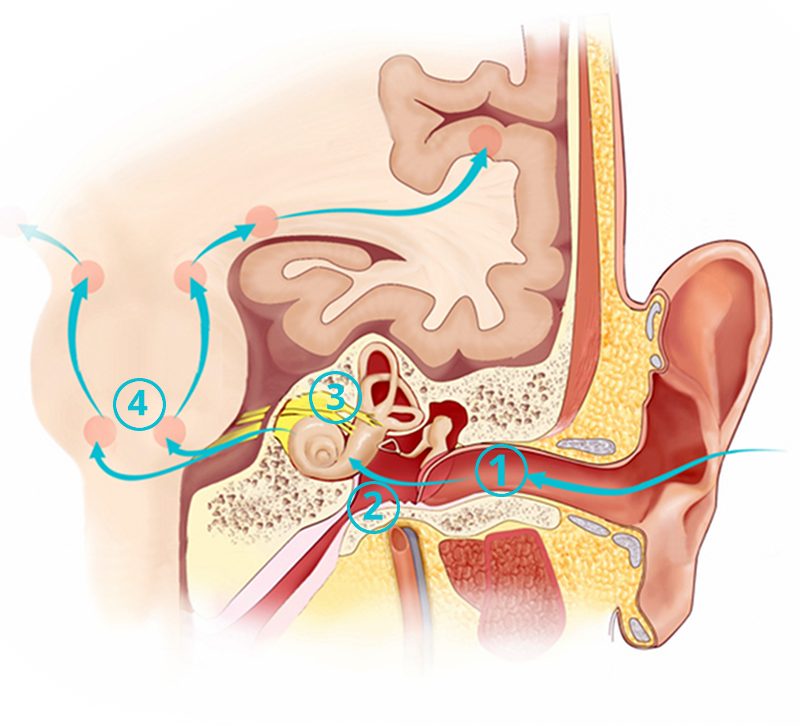
Grossièrement cela fonctionne de la manière suivante : le son (ou plutôt l’onde sonore) traverse l’oreille externe où se trouvent le pavillon et le conduit auditif. Elle percute alors le tympan qui marque le début de l’oreille moyenne. Cette dernière augmente la pression de l’onde grâce à un muscle et trois petits os : l’enclume, le marteau et l’étrier. L’onde percute alors la cochlée (en forme d’escargot), qui se trouve dans l’oreille interne. Son rôle est de transformer l’onde mécanique en signal électrique grâce à des cellules ciliées. Ce signal est ensuite transmis au cerveau grâce à un réseau de nerfs.
Mais ce n’est pas tout ! Comme de nombreuses parties de notre corps, l’oreille se dégrade de façon irréparable au cours de notre vie. On lit souvent que notre oreille est capable d’entendre les sons entre 20Hz et 20kHz, mais cela dépend de l’état de votre système auditif. Cette plage de fréquence est réaliste pour un jeune en bonne santé, mais avec les années qui s’accumulent on perd rapidement en capacité d’ouïe. Cette perte est d’autant plus rapide que vous écoutez des sons forts, longtemps et purs. Quelques conseils pour prolonger un peu votre audition :
- Temps d’écoute : essayer de reposer de temps en temps vos oreilles en vous ménageant des temps de pauses réguliers.
- Volume sonore : allez-y molo sur le volume des casques et des écouteurs. En france il existe une limite de puissance pour les écouteurs et les casques, mais elle est déjà très haute ! En discothèque ou en concert portez de boules quies. Il existe des modèles non jetables réalisés sur-mesures qui sont plus agréables à porter que ceux du commerce.
- Au travail aussi il existe des normes de bruits acceptables en fonction de votre métier. L’employeur doit dans certains cas fournir des dispositifs de protection individuels. Renseignez-vous

- Tous les ans vous pouvez vous rendre chez un professionnel de l’audition pour réaliser un bilan auditif. Lors de certaines opérations ils sont parfois proposés gratuitement.
Décibel et niveaux sonores
En acoustique on utilise le décibel (dB) pour mesurer la force d’un son. Le décibel nous permet de quantifier la pression acoustique d’un son. Comme il s’agit d’une pression on aurait aussi pu travailler avec des Pascals, des Bars ou des PSI, mais le problème est la finesse de notre oreille. En effet elle est capable d’entendre des sons d’une pression de $ 2*10^-5 Pa $ à $ 20 Pa $. Pas très pratique de travailler sur une aussi grande échelle de valeur. C’est pour cela que le décibel a été inventé. Contrairement au Pascal il n’utilise pas une échelle linéaire, mais une échelle logarithmique. De plus, cela correspond à la façon dont notre oreille entend la puissance des sons.
Pour ceux qui n’ont jamais travaillé avec ce type d’outils, bienvenue dans un monde ou 50dB + 50dB ne fait pas 100dB. Voici quelques règles de calcul pour vous aider.
On utilise la pression acoustique (ou le niveau sonore) pour quantifier la puissance d’un son.
Que l’on peut aussi écrire
Si on utilise les règles vues ci-dessus, on obtient :
Avec $P_0$ la pression acoustique de référence, soit $2 \cdot 10^-5$ et $P$ la pression du son dont on veut obtenir le niveau sonore. Notez bien que ces deux formules sont équivalentes, dans un cas on travaille avec la pression et dans l’autre cas avec la puissance du son (pression élevée au carré).
Voyons maintenant quelques ordres de grandeurs pour se familiariser avec les décibels. Garder en tête que ces valeurs sont approximatives car elles dépendent du point d’écoute.
|
Niveau sonore |
Exemple |
|---|---|
|
0dB |
Seuil d’audition |
|
40dB |
Bruit d’ambiance de bibliothèque |
|
65dB |
Bruit d’ambiance de bureau |
|
110dB |
Orchestre symphonique à fortissimo |
|
140dB |
Seuil de douleur (saignements) |
Notez que même si le seuil de douleur se trouve entre 130dB et 140dB, les dommages sont causés avant sur votre appareil auditif. En France la loi considère que dans un environnement de travail, des protections auditives doivent être fournies si l’humain est exposé à un bruit de 85dB ou plus pendant une journée de travail en continu.
Additionner deux niveaux sonores
Dans ces exemples on se place dans des cas simplifiés. Les fréquences des deux ondes sont identiques et les ondes sont en phase. C’est-à-dire quelles sont synchronisées, que les ondes atteignent leurs maximum et leurs minimum en même temps.
Exemple 1
Si je perçois deux sons ayant chacun un niveau sonore de 50dB, quel sera le niveau sonore résultant ?
Bonne question ! Si vous avez suivi, vous savez que la réponse n’est pas 100dB. On considère que l’on entend deux sons de pression acoustique $P_1$, on a :
Or
D’où :
Voici donc la première règle à retenir en acoustique :
Quand on ajoute deux sons de même pression acoustique $P_1$, la pression acoustique résultante est 3dB supérieure à $P_1$.
Exemple 2
Plaçons-nous maintenant dans le cas de deux sons de pressions acoustiques différentes. Imaginons un son perçu à 65dB et un autre à 80dB, qu’elle sera la pression acoustique du son résultant ?
On se sert à nouveau des logarithmes.
De même avec la deuxième source, on obtient
Or
D’où
On note que cette fois-ci le résultat est quasiment équivalent à la puissance de la source principale. En effet, nous avons vu que l’ajout d’une source identique donne un résultat à $+3db$. L’ajout d’une source de puissance bien inférieure est à peine caractérisable sur l’échelle logarithmique.
La puissance des sources
La puissance acoustique (aussi exprimée en dB) nous permet de caractériser une source (enceinte, machine, voiture, etc.) en définissant la puissance du son quelle émet. Elle est définie par :
Avec $P$ la puissance acoustique de la source en Watt et $P_0$ la pression de référence de 12 Watts. La formule ressemble fortement à celle de la pression acoustique faites attention à ne pas vous mélanger les pinceaux.
En extérieur
Maintenant que nous avons vu la pression acoustique et la puissance acoustique, voyons comment les relier. Imaginons que nous sommes en extérieur à 3m d’une enceinte rayonnant de la même façon dans toutes les directions d’une puissance sonore de 65dB. Quelle pression acoustique allons-nous ressentir ? Nous allons utiliser la relation suivante :
Avec $r$ la distance entre la source et et le point d’écoute. On trouve directement le résultat suivant :
Ce qui donne :
Cette formule ne fonctionne que dans le cas du champ libre, c’est-à-dire le cas où l’onde sonore ne rencontre aucun obstacle. On remarque que la pression acoustique dépend de la distance d’écoute. Plus on s’écarte de la source plus la pression acoustique est faible, cela correspond bien à notre ressenti dans la vie de tous les jours.

Cette décroissance de la pression acoustique ne se fait pas au hasard. Prenons un exemple facile : quand vous jetez un cailloux dans l’eau, l’onde prend une forme de cercle qui a pour centre le point de chute du cailloux. On dit que le front d’onde est un cercle. Autrement dit tous les points de ce cercle sont dans le même état au même moment. Ils sont en « haut de la vague » au même moment. Dans cet exemple notre onde se propage sur un plan, celui de l’eau. Mais dans notre cas, on travaille dans un espace à trois dimensions… Avez-vous remarqué le $4\pi r^ 2$ qui apparait dans la formule ? Il s’agit de la formule de la surface d’une sphère de rayon $r$. Vous l’avez deviné notre front d’onde dans l’espace est une sphère et non plus un cercle. Tous les points de cette sphère ont la même pression acoustique au même moment. L’onde se propage de manière semblable dans toutes les directions.
Imaginons maintenant que l’enceinte est posée par terre, son front d’onde ne peut plus être une sphère car le sol bloque la propagation de l’onde. Le front d’onde résultant est une demi-sphère, le sol en dessous de l’enceinte n’est plus concerné par le calcul. Pour ce cas, on peut utiliser la même formule en introduisant un coefficient de directivité $Q$ . On se retrouve avec :
Dans notre cas de la demi-sphère $Q=2$, on obtient :
$ L_p = 42,46db $ soit un gain de $3db$.
En intérieur
Maintenant le même cas dans une pièce de 75m3. On peut utiliser la relation suivante.
$L_p = L_w - 5 \cdot \log_{10}(V) - 10 \cdot \log_{10}(r) + 3$
Avec $r$ la distance entre le point d’écoute et la source en mètres et $V$ le volume de pièce en m 3.
$L_p = 65 - 5 \cdot \log_{10}(75) - 10 \cdot \log_{10}(3) + 3$
Ce calcul, n’est qu’une approximation et dépend de beaucoup de détails sur la source et la pièce. Cela permet d’obtenir un ordre d’idée dans une pièce avec une réverbération moyenne.
J’espère qu’avec ces exemples vous avez bien compris la différence entre la pression acoustique que l’on ressent $L_p$ et la puissance émise par une source $L_w$.
Bien sûr ces relations ne sont que des approximations, car un tel calcul dépend de nombreuses variables (vent, forme de la pièce, directivité de l’enceinte, matériaux de la pièce, etc.).
La mesure du son et la réverbération
La mesure du son
Les chiffres donnés sans contexte, sans unité ou sans méthode de mesure peuvent parfois être trompeurs. Un monde où l’on trouve beaucoup de mesures acoustiques est celui de électronique et de l’électroménager (bruit d’un mixeur, d’un ordinateur, d’un aspirateur, etc.). En effet, aujourd’hui les fiches techniques d’électroménager présentent le bruit produit par l’appareil. Mais, en général rien n’est indiqué quant à la mesure. Voyons voir comment tricher un peu avec les chiffres.
Les courbes de pondération
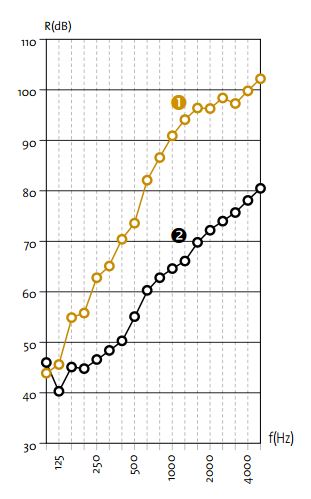
On a vu qu’en acoustique, tous les sons sont mesurés en décibels. Pour des raisons pratiques ils arrivent aux acousticiens de créer des courbes de pondérations qui permettent d’ajuster le décibel à certains usages. En effet notre oreille ne perçoit pas les fréquences de la même façon en fonction du niveau sonore. Par exemple, un bruit assez faible dans les basses fréquences ne sera pas perçu, alors qu’un bruit avec la même puissance acoustique dans les hautes fréquences sera perçu. Pour se rapprocher de la réalité il existe donc des courbes de pondération des décibels en fonctions de la puissance du son. Ces courbes sont repérées par des lettres que l’on accole derrière le décibel (dBa, dBb, dBc, etc.). Voici à quoi ressemblent ces courbes.

Malheureusement la courbe de pondération utilisée lors des mesures n’est pas toujours indiquée…
La position de la mesure
Autre chose parfois aberrante, on ne connait pas la distance de la mesure effectuée. Généralement on peut considérer que la mesure est faite à 1m de la source, mais ce n’est pas toujours le cas. Dernière petite remarque, on ne connait jamais la position du micro réalisant la mesure. Pourtant les objets ne produisent pas du son de manière équivalente dans toutes les directions. Pas convaincu ? Approchez votre oreille de l’avant de votre ordinateur, puis des côtés, puis de l’arrière. Je suis sûr qu’un côté produit plus de bruit que l’autre, celui où se trouve la ventilation. À quoi servent toutes ces mesures de bruit si on ne connait pas le point de mesure? Par exemple dans le cas d’une machine à laver ce qui intéresse le consommateur est le bruit devant la machine. Mais peut-être que la mesure est réalisée derrière, voire même en dessous, si cela permet au constructeur de présenter des données plus avantageuses. Bref ces données sont vraiment à prendre avec des pincettes!
La réverbération
Pour finir cette petite introduction à l’acoustique, intéressons-nous à un phénomène amusant : la réverbération, plus communément appelé écho. Cette sensation de son qui « dure » (ou qui « revient ») provient de l’environnement dans lequel on se trouve. Vous entendrez facilement de l’écho devant une falaise ou dans une pièce vide, mais jamais en plein milieu d’un champ.
En effet ce phénomène se produit à cause de la réflexion de l’onde sonore sur une surface. Voyons voir ce qui rend un milieu réverbérant.
Les matériaux
Certains matériaux ont un pouvoir de réflexion des ondes beaucoup plus important que d’autres. Par exemple un mur en béton lisse renvoi quasiment 100% de l’onde sonore. Autrement dit, il a un coefficient d’absorption proche de 0. De la moquette en revanche absorbe presque 30% de l’onde sonore, elle a un coefficient d’absorption de 0,3. Comme vous l’imaginez facilement, une matière dure aura un coefficient d’absorption faible alors que les matières molles (tissus, mousses, etc.) absorbent beaucoup.
Il s’agit là en fait d’une approche simpliste car le coefficient d’absorption dépend de la fréquence du son. On regarde en général le coefficient pour cinq ou six fréquences différentes afin de voir s’il absorbe mieux les aiguës ou les graves.
La forme
La forme de la surface de rebond à aussi une importance. Dans une pièce meublée, les ondes sonores de votre voix vont « rebondir » sur des objets aux formes variées. Ces objets sont alors émetteurs secondaires, mais émettent dans toutes les directions. L’onde sonore de base se disperse donc dans le milieu. En revanche face à un mur plat, votre onde sonore est majoritairement renvoyée vers vous (au coefficient de réverbération près). L’onde n’est pas diffractée et l’écho se fait beaucoup plus ressentir.
Temps de réverbération
Savoir avant la construction d’une pièce si celle-ci sera réverbérante ou non est assez compliqué. En général les acousticiens utilisent des logiciels de modélisation acoustique 3D pour obtenir un ordre d’idée. En revanche, quantifier la réverbération d’une salle que l’on à sous la main est un jeu d’enfant.
Pour cette opération on utilise une enceinte qui émet un son assez fort et on mesure avec un micro le temps nécessaire après l’arrêt de l’émission pour que le niveau sonore de la salle descende de 60dB. Voici le genre de courbe que l’on mesure.

On appelle cette méthode de mesure le temps de réverbération à -60dB ou encore le temps de réverbération Sabine, du nom de Wallace Clément Sabine, premier scientifique s’étant intéressé aux phénomènes d’échos. À noter qu’aux débuts de ses recherche, en absence de dispositif de mesure il effectuait ses tests à l’oreille  .
.
Il existe un record du monde de l’écho le plus long du monde avec un temps de réverbération de 112 secondes.
Il existe des pièces conçues spécialement pour la mesure sonore appelées chambre anéchoïque (ou chambre sourde) et qui présentent la caractéristique de n’avoir aucune réverbération (ou presque). Pour cela ces salles sont construites de manière très spéciale : murs non-parallèles, surfaces cassantes, matériaux absorbants, etc. Si vous souhaitez en utiliser une, sachez que l’IRCAM à Paris possède une chambre anéchoïque ouverte au public.
Nous avons vu dans cet article les bases de l’acoustique, de l’onde sonore à la réverbération. Il s’agit d’une introduction, il est donc possible d’approfondir certains thèmes comme l’acoustique des salles, le fonctionnement des enceintes ou la captation sonore à l’aide de micros. On peut aussi s’intéresser à la vie du signal sonore analogique et numérique, avec des sujets comme la compression MP3.
J’espère que j’ai su vous transmettre ma passion pour l’acoustique. Sachez que si vous souhaitez en savoir plus, certaines notions nécessitent d’être à l’aise avec les logarithmes et la manipulation d’ondes sinusoïdales.
En savoir plus
- Acoustique : Propagation en champ libre. Introduction à l’acoustique en architecture par Ricardo Atienza, Suzel Balez et Nicolas Remy.
- Le fonctionnement d’un microphone, sur Zeste de Savoir.
- Designing and building a low-nois hemi-anechoic chamber (en). Publié par l’acoustical society of america.
- icône libre issue du logiciel audacity.


