Connaissez-vous l’apprentissage automatique, ou machine learning en anglais ? Concrètement, il s’agit d’une branche de l’informatique, qui englobe les algorithmes qui apprennent par eux-mêmes. Apprendre par soi-même, qu’est-ce que cela veut dire ? Tout simplement qu’au début, un algorithme de d’apprentissage automatique ne sait rien faire ; puis, au fur et à mesure qu’il s’entraîne sur des données, il est capable de répondre de plus en plus efficacement à la tâche qu’on lui demande de faire. Un peu comme vous et moi, en quelque sorte.
On peut ainsi classer les algorithmes en deux catégories :
- les algorithmes « classiques », où l’algorithme se contente d’appliquer une série de règles sans apprendre des cas précédents ;
- les algorithmes d’apprentissage automatique, où l’algorithme est capable d’effectuer un apprentissage à partir des données déjà vues.
Aujourd’hui, nous allons parler de machine learning, et plus particulièrement de la famille des SVM.
Mais avant toute chose, un SVM, c’est quoi ? Derrière ce nom barbare (qui est l’acronyme de Support Vector Machines, soit machines à vecteurs support en français, parfois traduit par séparateur à vaste marge pour garder l’acronyme) se cache un algorithme d’apprentissage automatique, et qui est très efficace dans les problèmes de classification. Cela ne vous dit rien ? Ça tombe bien, on va justement voir ce que c’est.
Dans un premier temps, nous allons découvrir les grands principes qui sous-tendent les SVM.
Ensuite, nous allons nous plonger dans les mathématiques qui font toute la beauté de la chose ! Pour cette partie (qui peut être sautée si les maths ne sont pas votre tasse de thé), vous aurez besoin d’être familier avec les bases de l’algèbre linéaire (espace vectoriel de dimension , produit scalaire, norme euclidienne).
Enfin, nous reviendrons à du concret, avec les généralisations du SVM, et un exemple pratique pour faire joujou !
Prêt ? C’est parti !
- Problème de classification, SVM : C'est quoi, au juste ?
- Les SVM, dans les grandes lignes
- Formalisme des SVM
- Entraînement des SVM
- Systèmes non linéaires ; astuce du noyau
- Cas non-séparable
- Tester l'entraînement d'un SVM
- SVM multiclasse
- A vous de jouer !
Problème de classification, SVM : C'est quoi, au juste ?
Avant toute chose, nous allons commencer par établir un cadre à ce que nous allons voir. En particulier, qu’est-ce qu’un problème de classification ?
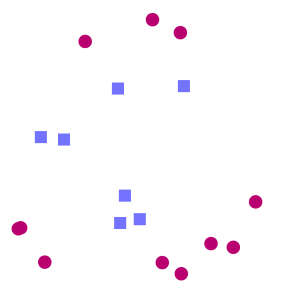
Considérons l’exemple suivant. On se place dans le plan, et l’on dispose de deux catégories : les ronds rouges et les carrés bleus, chacune occupant une région différente du plan. Cependant, la frontière entre ces deux régions n’est pas connue. Ce que l’on veut, c’est que quand on lui présentera un nouveau point dont on ne connaît que la position dans le plan, l’algorithme de classification sera capable de prédire si ce nouveau point est un carré rouge ou un rond bleu.
Voici notre problème de classification : pour chaque nouvelle entrée, être capable de déterminer à quelle catégorie cette entrée appartient.
Autrement dit, il faut être capable de trouver la frontière entre les différentes catégories. Si on connaît la frontière, savoir de quel côté de la frontière appartient le point, et donc à quelle catégorie il appartient.

Le SVM est une solution à ce problème de classification1. Le SVM appartient à la catégorie des classificateurs linéaires (qui utilisent une séparation linéaire des données), et qui dispose de sa méthode à lui pour trouver la frontière entre les catégories.
Pour que le SVM puisse trouver cette frontière, il est nécessaire de lui donner des données d’entraînement. En l’occurrence, on donne au SVM un ensemble de points, dont on sait déjà si ce sont des carrés rouges ou des ronds bleus, comme dans la Figure 1. A partir de ces données, le SVM va estimer l’emplacement le plus plausible de la frontière : c’est la période d'entraînement, nécessaire à tout algorithme d’apprentissage automatique.
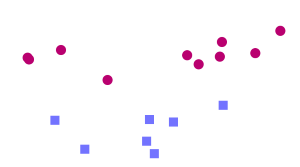
Une fois la phase d’entraînement terminée, le SVM a ainsi trouvé, à partir de données d’entraînement, l’emplacement supposé de la frontière. En quelque sorte, il a « appris » l’emplacement de la frontière grâce aux données d’entraînement. Qui plus est, le SVM est maintenant capable de prédire à quelle catégorie appartient une entrée qu’il n’avait jamais vue avant, et sans intervention humaine (comme c’est le cas avec le triangle noir dans la Figure 2) : c’est là tout l’intérêt de l’apprentissage automatique.

Comme vous pouvez le constater dans la figure ci-dessus, pour notre problème le SVM a choisi une ligne droite comme frontière2. C’est parce que, comme on l’a dit, le SVM est un classificateur linéaire. Bien sûr, la frontière trouvée n’est pas la seule solution possible, et n’est probablement pas optimale non plus.
Cependant, il est considéré que, étant donné un ensemble de données d’entraînement, les SVM sont des outils qui obtiennent parmi les meilleurs résultats. En fait, il a même été prouvé que dans la catégorie des classificateurs linéaires, les SVM sont ceux qui obtiennent les meilleurs résultats.
Un des autres avantages des SVM, et qu’il est important de noter, est que ces derniers sont très efficaces quand on ne dispose que de peu de données d’entraînement : alors que d’autres algorithmes n’arriveraient pas à généraliser correctement, on observe que les SVM sont beaucoup plus efficaces. Cependant, quand les données sont trop nombreuses, le SVM a tendance à baisser en performance.
Maintenant que nous avons défini notre cadre, nous pouvons partir à l’assaut des SVM. En route !
Les SVM, dans les grandes lignes
Bon, nous savons donc que le but, pour un SVM, est d’apprendre à bien placer la frontière entre deux catégories. Mais comment faire ? Quand on a un ensemble de points d’entraînement, il existe plusieurs lignes droites qui peuvent séparer nos catégories. La plupart du temps, il y en a une infinité… Alors, laquelle choisir ?

Intuitivement, on se dit que si on nous donne un nouveau point, très proche des ronds rouges, alors ce point a de fortes chances d’être un rond rouge lui aussi. Inversement, plus un point est près des carrés bleus, plus il a de chances d’être lui-même un carré bleu. Pour cette raison, un SVM va placer la frontière aussi loin que possible des carrés bleus, mais également aussi loin que possible des ronds rouges.

Comme on le voit dans la figure 4, c’est bien la frontière la plus éloignée de tous les points d’entraînement qui est optimale, on dit qu’elle a la meilleure capacité de généralisation. Ainsi, le but d’un SVM est de trouver cette frontière optimale, en maximisant la distance entre les points d’entraînement et la frontière.
Les points d’entraînement les plus proches de la frontière sont appelés vecteurs support, et c’est d’eux que les SVM tirent leur nom : SVM signifie Support Vector Machine, ou Machines à Vecteur Support en français. Support, parce que ce sont ces points qui « supportent » la frontière. Vecteurs, parce que… on en reparlera plus tard, dans les explications mathématiques (quel teasing !).
Ça, c’est pour les principes de base. En théorie, ça suffit, mais en pratique… En effet, les SVM sont conçus de telle manière que la frontière est forcément, dans notre exemple, une ligne droite. Et ça, c’est loin d’être suffisant pour la plupart des cas.
Considérons l’exemple suivant.
Puisque les carrés sont entourés de ronds de toute part, il est impossible de trouver de ligne droite qui soit une frontière : on dit que les données d’entraînement ne sont pas linéairement séparables. Cependant, imaginez qu’on arrive à trouver une transformation qui fasse en sorte que notre problème ressemble à ça :
A partir de là, il est facile de trouver une séparation linéaire. Il suffit donc de trouver une transformation qui va bien pour pouvoir classer les objets. Cette méthode est appelée kernel trick, ou astuce du noyau en français. Vous vous en doutez, toute la difficulté est de trouver la bonne transformation…
Bien ! Nous savons maintenant quel est le but d’un SVM, et quelles sont les grandes idées qui sous-tendent l’ensemble. Il est maintenant temps de se plonger dans le bain, avec une formalisation du problème. Si les maths ne vous attirent pas, ne partez pas tout de suite ! Vous pouvez directement passer à la partie « Cas non-séparable » et les suivantes, où nous allons voir des améliorations du SVM. Dans le cas contraire, suivez le guide.
Formalisme des SVM
De façon plus générale que dans les exemples donnés précédemment, les SVM ne se bornent pas à séparer des points dans le plan. Ils peuvent en fait séparer des points dans un espace de dimension quelconque. Par exemple, si on cherche à classer des fleurs par espèce, alors que l’on connaît leur taille, leur nombre de pétales et le diamètre de leur tige, on travaillera en dimension 3.
Un autre exemple est celui de la reconnaissance d’image : une image en noir et blanc de 28*28 pixels contient 784 pixels, et est donc un objet de dimension 784. Il est ainsi courant de travailler dans des espaces de plusieurs milliers de dimensions.
Fondamentalement, un SVM cherchera simplement à trouver un hyperplan qui sépare les deux catégories de notre problème.
Précisions sur les hyperplans
Dans un espace vectoriel de dimension finie , un hyperplan est un sous-espace vectoriel de dimension . Ainsi, dans un espace de dimension un hyperplan sera une droite, dans un espace de dimension un hyperplan sera un plan, etc.
Soit un espace vectoriel de dimension . L’équation caractéristique d’un hyperplan est de la forme , où sont des scalaires. Par définition, tout vecteur vérifiant l’équation appartient à l’hyperplan. Par exemple, en dimension , est bien l’équation caractéristique d’une droite vectorielle (qui passe par l’origine).
De plus, un hyperplan sépare complètement l’espace vectoriel en deux parties distinctes. Ainsi, une ligne droite sépare le plan en deux régions distinctes ; et en dimension , c’est le plan qui joue le rôle de ce séparateur : il y a un demi-espace « d’un côté » du plan, et un autre demi-espace « de l’autre côté » du plan. Avec un hyperplan, il est donc possible de diviser notre espace vectoriel en deux catégories distinctes : tout pile ce qu’il nous faut pour notre problème de classification !
Comme vous pouvez le constater, un hyperplan vectoriel passe toujours par . C’est pour cette raison qu’on utilisera un hyperplan affine, qui n’a pas quant à lui obligation de passer par l’origine.
Ainsi, si l’on se place dans , pendant son entraînement le SVM calculera un hyperplan vectoriel d’équation , ainsi qu’un scalaire (un nombre réel) . C’est ce scalaire qui va nous permettre de travailler avec un hyperplan affine, comme nous allons le voir.
Le vecteur est appelé vecteur de poids, le scalaire est appelé biais.
Une fois l’entraînement terminé, pour classer une nouvelle entrée , le SVM regardera le signe de :
Si est positif ou nul, alors est d’un côté de l’hyperplan affine et appartient à la première catégorie, sinon est de l’autre côté de l’hyperplan, et donc appartient à la seconde catégorie.
En résumé, on souhaite savoir, pour un point , s’il se trouve d’un côté ou de l’autre de l’hyperplan. La fonction nous permet de répondre à cette question, grâce à la classification suivante :
Entraînement des SVM
Ainsi, étant donnés un hyperplan de vecteur de poids , et de biais , nous pouvons calculer si un point appartient à telle ou telle catégorie, grâce au signe de .
En particulier, supposons que l’on assigne à tout point un label qui vaut si appartient à la première catégorie, et si appartient à la seconde catégorie. Alors, si le SVM est correctement entraîné, on a toujours , c’est-à-dire .
Le but d’un SVM, lors de l’entraînement, est donc de trouver un vecteur de poids et un biais tels que, pour tout de label appartenant aux données d’entraînement, . Autrement dit, de trouver un hyperplan séparateur entre les deux catégories.

Comme on l’a vu précédemment, on choisira l’hyplerplan qui maximise la marge, c’est-à-dire la distance minimale entre les vecteurs d’entraînement et l’hyperplan. De tels vecteurs situés à la distance minimale sont appelés vecteurs supports.
C’est de là que vient le nom des SVM. En effet, on peut prouver que l’hyperplan donné par un SVM ne dépend que des vecteurs supports, c’est donc tout naturellement qu’on a appelé cette structure les Support Vectors Machines, c’est-à-dire les machines à vecteur support.
Calcul de la marge
Si l’on prend un point , on peut prouver que sa distance à l’hyperplan de vecteur support et de biais est donnée par1 :
où désigne la norme euclidienne de . La marge d’un hyperplan de paramètres par rapport à un ensemble de points est donc . Pour rappel, la marge est la distance minimale de l’hyperplan à un des points d’entraînement.
Maximisation de la marge
On veut trouver l’hyperplan de support et de biais qui permettent de maximiser cette marge, c’est-à-dire qu’on veut trouver un hyperplan avec la plus grande marge possible. Cela permettra, intuitivement, d’être tolérant face aux petites variations.
Cette intuition est justifiée : en 1995, le Russe Vladimir Vapnik a prouvé que cette maximisation produit un hyperplan optimal, c’est-à-dire qui donnera lieu au moins d’erreurs possible (on parle de capacité de généralisation maximale).

Puisque l’on cherche l’hyperplan qui maximise la marge, on cherche l’unique hyperplan dont les paramètres sont donnés par la formule : .
Normalisation et résolution du problème
Même si on peut montrer que l’hyperplan optimal est unique, il existe plusieurs couples qui décrivent ce même hyperplan2. On décide de ne considérer que l’unique paramétrage tel que les vecteurs support vérifient . Par conséquent, , et l’égalité est atteinte si est un vecteur support. Dit autrement, cette normalisation sur et permet de garantir que la marge est alors de $ \frac 1{|w|}$.
Le problème d’optimisation de la marge se simplifie ainsi en , tout en gardant en tête nos hypothèses de normalisation, à savoir .
On se retrouve donc avec le problème suivant :
Que l’on peut reformuler de la façon suivante :
Que, pour des raisons pratiques, on reformule à nouveau :
Ce genre de problème est appelé problème d’optimisation quadratique, et il existe de nombreuses méthodes pour le résoudre. Dans le cas présent, on utilise la méthode des multiplicateurs de Lagrange, que le lecteur intéressé pourra consulter sur ce PDF (en anglais).
Cette résolution donnera une valeur optimale pour , mais rien pour . Pour retrouver , il suffit de se rappeler que pour les vecteurs support, . On en déduit donc que est tel que .
Notre SVM est à présent entraîné, et nous pouvons l’utiliser pour classer des données qu’il n’avait jusqu’à présent jamais vues (en utilisant notre fonction de classification ). Félicitations ! Vous savez désormais comment fonctionne un SVM, comment l’entraîner, et comment s’en servir.
- La distance d’un point à un hyperplan , avec un biais , est donnée par la formule . Or, montre facilement que pour un hyperplan séparateur, , d’où la formule. ↩
- En effet, vous pouvez vérifier par vous-mêmes que si un hyperplan est décrit par les paramètres , alors est également décrit par les paramètres , pour tout réel non nul .↩
Systèmes non linéaires ; astuce du noyau
Abordons maintenant le problème des données non linéairement séparables. Pour rappel, des données sont non linéairement séparables quand il n’existe pas d’hyperplan capable de séparer correctement les deux catégories. Ce qui, d’ailleurs, arrive quasiment tout le temps en pratique.

Plongée en dimension supérieure
Pour contourner le problème, l’idée est donc la suivante : il est impossible de séparer linéairement les données dans notre espace vectoriel ? Qu’importe ! Essayons dans un autre espace. De façon générale, il est courant ne pas pouvoir séparer les données parce que l’espace est de trop petite dimension1. Si l’on arrivait à transposer les données dans un espace de plus grande dimension, on arriverait peut-être à trouver un hyperplan séparateur.
Je sens que j’en ai perdu quelques-uns en cours de route.
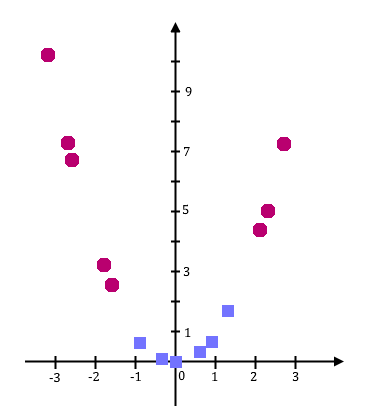
Considérons l’exemple suivant, qui vous aidera à mieux comprendre. Je souhaite construire un SVM qui, à partir de la taille d’un individu, me dit si cet individu est un jeune adolescent (entre 12 et 16 ans, carrés bleus) ou non (ronds rouges).

On constate que l’on ne peut pas trouver d’hyperplan séparateur (ici, on est en dimension 1, un hyperplan séparateur est donc un simple point). Ce qui est embêtant : si l’on ne peut pas trouver d’hyperplan séparateur, notre SVM ne sera pas capable de s’entraîner, et encore moins de classer de nouvelles entrées…
On essaie donc de trouver un nouvel espace, généralement de dimension supérieure, dans lequel on peut projeter nos valeurs d’entraînement, et dans lequel on pourra trouver un séparateur linéaire.
Dans cet exemple, je vous propose d’utiliser la projection . On passe donc de l’espace vectoriel , de dimension 1, à l’espace vectoriel , de dimension 2.
On se retrouve donc avec les données d’entraînement suivantes :
On voit que les données sont alors linéairement séparables : notre SVM va pouvoir fonctionner !
Plus formellement, l’idée de cette redescription du problème est de considérer que l’espace actuel, appelé espace de description, est de dimension trop petite ; alors que si on plongeait les données dans un espace de dimension supérieure, appelé espace de redescription, les données seraient linéairement séparables.
Bien sûr, il ne suffit pas d’ajouter des dimensions à l’espace de description, cela ne résoudrait d’ailleurs rien. Il faut au contraire redistribuer les points depuis l’espace de description vers l’espace de redescription, à l’aide d’une fonction , nécessairement non-linéaire.
On définit l’opération de redescription des points de vers par l’opération :
Dans ce nouvel espace , on va tenter d’entraîner le SVM, comme nous l’aurions fait dans l’espace . Si les données y sont linéairement séparables, c’est gagné ! Par la suite, si l’on veut classer , il suffira de classer : on obtient ainsi un SVM fonctionnel.
L’astuce du noyau pour simplifier les calculs
Malheureusement, plus on se plonge dans une grande dimension, plus les calculs sont longs. Alors, si on se plonge en dimension infinie… Néanmoins, il est possible de simplifier les calculs. Quand on pose le problème d’optimisation quadratique dans l’espace , on s’aperçoit que les seules apparitions de sont de la forme . De même dans l’expression de la fonction de classification . Par conséquent, il n’y a pas besoin de connaître expressément , ni même : il suffit de connaître toutes les valeurs , qui ne dépendent donc que des .
On appelle donc fonction noyau la fonction définie de la façon suivante : . A ce moment, le calcul de l’hyperplan séparateur dans ne nécessite ni la connaissance de , ni de , mais seulement de .
Par exemple, supposons que soit l’espace de description, de dimension ; et que l’espace de redescription soit de dimension . Le calcul de se fait en , tandis que le calcul de , qui donne le même résultat, se fait en , d’où un avantage en temps de calcul immédiat.
C’est de ce constat qu’arrive le kernel trick, ou astuce du noyau. Puisque l’on n’a besoin que de connaître , pourquoi ne pas utiliser un quelconque, qui correspond à une redescription quelconque, et de résoudre le problème de séparation linéaire sans même se soucier de l’espace de redescription dans lequel on évolue ?
Grâce au théorème de Mercer, on sait qu’une condition suffisante pour qu’une fonction soit une fonction noyau est que soit continue, symétrique et semi-définie positive.
Noyau symétrique semi-défini positif
Une fonction est dite symétrique si et seulement si, (dans le cas où est à deux variables).
Une fonction symétrique est dite semi-définie positive si et seulement si, pour tout ensemble fini , et pour tous réels , .
Par exemple, le produit scalaire usuel est semi-défini positif, car il est symétrique et .
Ainsi, il est possible d’utiliser n’importe quelle fonction noyau afin de réaliser une redescription dans un espace de dimension supérieure. La fonction noyau étant définie sur l’espace de description (et non sur l’espace de redescription , de plus grande dimension), les calculs sont beaucoup plus rapides.
Voici une liste non exhaustive de noyaux couramment utilisés.
- Le noyau polynomial,
- Le noyau gaussien,
- Le noyau laplacien,
- Le noyau rationnel,
Chacun possède ses avantages et ses inconvénients, qui sont décrits dans cet article (en anglais). C’est donc à l’utilisateur de choisir le noyau, et les paramètres de ce noyau, qui correspond le mieux à son problème. Et comment choisir son noyau, me demanderez-vous ? Eh bien… Je n’ai pas de méthode à vous donner, ça dépend énormément de votre jeu de données. Avec l’expérience, certains noyaux deviennent plus intuitifs que d’autres dans certains problèmes.
Pour résumer, voici les quatre grandes idées à la base du kernel trick :
- Les données décrites dans l’espace d’entrée sont projetées dans un espace de redescription .
- Des régularités linéaires sont cherchées dans cet espace .
- Les algorithmes de recherche n’ont pas besoin de connaître les coordonnées des projections des données dans , mais seulement leurs produits scalaires.
- Ces produits scalaires peuvent être calculés efficacement grâce à l’utilisation de fonctions noyau.
- En fait, on peut montrer qu’avec des données aléatoires, quand on travaille en dimension , il devient de plus en plus dur de trouver un hyperplan séparateur quand on dépasse valeurs d’entraînement. C’est le Cover’s theorem (en anglais)↩
Cas non-séparable
Nous savons ainsi que quand les données ne sont pas linéairement séparables, on peut toujours recourir au kernel trick, qui avec un peu de chance, nous permettra de séparer linéairement nos données. Est-ce toujours possible de trouver un bon noyau ?
Malheureusement, la réponse est non. Il existe des ensembles qui sont non séparables, peu importe les transformations qu’on lui fasse subir. Pour s’en convaincre, reprenons l’exemple précédent, avec les tailles des jeunes ados. D’un côté, René, 14 ans, est un ado dans toute sa splendeur, et mesure 1m50. De l’autre côté, Lucile n’est pas bien grande : malgré ses 20 ans, elle ne mesure que 1m50.
Dans un tel cas, il est impossible de différencier René de Lucile à partir de leur taille : aucun SVM ne pourra les séparer ; le problème est donc non séparable.
De plus, dans la plupart des cas en pratique, on n’arrive pas à trouver de kernel trick qui permette de séparer parfaitement les données. Et puis, on ne va pas non plus s’amuser à tous les tester un par un…
Pire encore, si l’ensemble de données d’entraînement n’est pas linéairement séparable, alors le problème d’optimisation quadratique sur lequel repose le SVM n’a pas de solution. Par conséquent, le SVM ne peut pas choisir d’hyperplan séparateur (de frontière), et donc ne marchera pas du tout. Et comme, dans la vraie vie, les données d’entraînement sont rarement linéairement séparables, même après kernel trick, on n’est pas sortis de l’auberge…
Mais ne vous inquétez pas ! Il est possible d’adapter le SVM, en rajoutant une notion de variable ressort (slack variable), qui autorise les erreurs de classification. Chaque erreur aura un coût, et le SVM tente alors de trouver l’hyperplan séparateur qui minimise le coût associé aux erreurs de classification, tout en maximisant la marge comme avant. Ainsi, notre SVM est capable de retourner un hyperplan séparateur qui marche (à peu près), que les données d’entraînement soient linéairement séparables ou non1.
En fait, dans la pratique, tout le monde utilise des SVM qui autorisent les erreurs de classifications : c’est littéralement impossible de travailler autrement en apprentissage automatique, que ce soit avec les SVM ou d’autres outils.
Je vous passe les détails mathématiques cette fois-ci. Si vous êtes curieux, vous pouvez regarder comment ça marche à partir de la page 19 de ce cours de Stanford (en anglais).
- Un SVM utilisant des slack variables peut tout à fait faire des erreurs de classification sur un ensemble de données d’entraînement qui est linéairement séparable (ça arrive quand le gain sur la marge est supérieur au coût engendré par les erreurs de classification). C’est particulièrement pratique pour ne pas être trop affecté par les valeurs extrêmes ou aberrantes (appelées outliers en anglais).↩
Tester l'entraînement d'un SVM
Maintenant que votre SVM est entraîné avec toutes les données d’entraînement, comment faire pour être sûr que votre SVM ne vous raconte pas de salades (c’est-à-dire, comment savoir si le SVM a bien été entraîné et ne commet pas trop d’erreurs) ?
La solution est de séparer aléatoirement ses données en deux groupes distincts.
Le premier groupe, appelé ensemble d’entraînement, sera utilisé pour entraîner notre SVM. Le second groupe, appelé ensemble de test, n’est pas utilisé lors de l’entraînement. On va en fait tester notre SVM sur chacune des entrées de l’ensemble de test : combien d’entrées on été correctement classées, une catégorie est-elle mieux reconnue que l’autre… ?
L’ensemble d’entraînement regroupe typiquement 80% de nos données, et l’ensemble de test contient les 20% restants. Il est capital que les données de test n’aient pas été utilisées pour entraîner le SVM, cela fausserait le résultat.
Pour plus de vérification, on peut utiliser une méthode supplémentaire, qui s’appelle la validation croisée. Ce tutoriel se voulant, originellement, être court (courage, c’est bientôt fini ), je vous redirige vers l'article Wikipédia. Plus d’informations sur la version anglaise.
SVM multiclasse
Enfin, jusque ici, nous n’avons vu que des SVM permettant de classer les données en deux catégories. Mais que se passe-t-il si nous avons plus que deux catégories ? Par exemple, supposons que je veuille entraîner un SVM à distinguer les abeilles, les guêpes et les frelons (savoir ce qui vient de me piquer ne va pas diminuer ma douleur, mais c’est toujours bon à savoir ), j’ai besoin d’un SVM qui sache distinguer trois classes différentes.
Si l’on reprend la définition rigoureuse de la frontière d’un SVM (un hyperplan qui sépare l’espace vectoriel en deux), on est bien embêtés : un hyperplan qui sépare l’espace vectoriel en trois (ou plus), ça n’existe pas… Mais comme bien souvent, les chercheurs qui se sont penchés sur le sujet ont trouvé des parades.
Il existe ainsi plusieurs méthodes d’adaptation des SVM aux problèmes multiclasses. Je ne vais parler que des approches one-vs-one et one-vs-all, parce que se sont les deux seules que je connais, et pour autant que je sache elles sont largement utilisées par la communauté.
Ces deux méthodes ne sont pas équivalentes : comme on va le voir, elles peuvent donner des résultats différents pour une même entrée, et avec les mêmes données d’entraînement.
One vs one
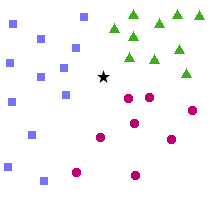
Dans cette approche, on va créer des « voteurs » : chaque voteur détermine si mon entrée a plus de chances d’appartenir à la catégorie ou à la catégorie . Ainsi, un voteur est un SVM qui s’entraîne sur les données de catégorie et uniquement.

Pour classer une entrée on retournera tout simplement la catégorie qui aura remporté le plus de duels. Ici, comme on le voit dans la figure 14, la catégorie « frelon » est celle qui remporte le plus de duels : j’ai donc été piqué par un frelon. Outch !

L’inconvénient de cette méthode est que le nombre de voteurs est globalement proportionnel au carré du nombre de catégories : pour 10 catégories, ce sont 45 voteurs qu’il faut créer, mais pour 20 catégories, il en faudra 190, d’où un temps de calcul de plus en plus élevé.
One vs all
L’approche one-vs-all consiste à créer un SVM par catégorie. Dans notre exemple, un SVM sera ainsi spécialisé dans la reconnaissance des abeilles, un autre dans la reconnaissance des guêpes, et un autre dans les frelons.
Pour entraîner mon SVM spécialisé en reconnaissance d’abeilles, je crée deux catégories : la catégorie « abeille », qui contient toutes les entrées d’abeilles, et la catégorie « pas abeille », qui contient toutes les autres entrées. Je fais de même pour mes SVM spécialisés dans les autres catégories.

Pour classer une nouvelle entrée, on regarde à quelle catégorie la nouvelle entrée est le plus probable d’appartenir.

Dans notre exemple, Figure 16, on voit que l’insecte m’ayant piqué est une abeille. Pôv' bête.
Il arrive que plusieurs SVM aient un résultat positif (par exemple, probablement une abeille, et probablement une guêpe). Dans ce cas-là, on prend celui qui est le plus certain de son résultat (c’est-à-dire celui pour lequel l’étoile est le plus éloignée de la frontière). De même, quand tous les résultats sont négatifs, on prend alors la catégorie du SVM pour lequel l’entrée est le plus près possible de la frontière (c’est-à-dire, celui pour lequel on est le moins sûr que le résultat est négatif).
En termes plus mathématiques, si l’on nomme les différentes fonctions de classification des SVM associés à nos catégories, l’entrée appartiendra à la catégorie , avec .
L’inconvénient de cette méthode est que, quand on commence à avoir beaucoup de données, on ne dispose (par exemple) que de 10 données « abeilles » contre 100 « pas abeilles ». Quand le déséquilibre entre la quantité de données dans les deux catégories est trop fort, un SVM obtient de moins bons résultats.
A vous de jouer !
Un SVM en action
Trève de théorie !
Je vous propose de tester un SVM, un vrai. Pour cela, voici un JSFiddle dont le code a été honteusement pompé sur la page d’accueil de la bibliothèque LibSVM.
Le SVM avec les paramètres que j’ai mis par défaut est un SVM avec un noyau linéaire (pas de kernel trick), qui autorise les erreurs (le coût est le nombre situé après -c dans la barre de texte). Il peut reconnaître trois classes différentes, avec une classification à la one-vs-one.
Cliquez sur la grille pour rajouter des points, cliquez sur le bouton « Changer de couleur » pour rajouter des points d’une autres couleur (rouge, jaune, bleu). La documentation de la barre de paramètres est donnée sur le site (en anglais), dont voici un copier-coller :
options:
-s svm_type : set type of SVM (default 0)
0 -- C-SVC
1 -- nu-SVC
2 -- one-class SVM
3 -- epsilon-SVR
4 -- nu-SVR
-t kernel_type : set type of kernel function (default 2)
0 -- linear: u'*v
1 -- polynomial: (gamma*u'*v + coef0)^degree
2 -- radial basis function: exp(-gamma*|u-v|^2)
3 -- sigmoid: tanh(gamma*u'*v + coef0)
-d degree : set degree in kernel function (default 3)
-g gamma : set gamma in kernel function (default 1/num_features)
-r coef0 : set coef0 in kernel function (default 0)
-c cost : set the parameter C of C-SVC, epsilon-SVR, and nu-SVR (default 1)
-n nu : set the parameter nu of nu-SVC, one-class SVM, and nu-SVR (default 0.5)
-p epsilon : set the epsilon in loss function of epsilon-SVR (default 0.1)
-m cachesize : set cache memory size in MB (default 100)
-e epsilon : set tolerance of termination criterion (default 0.001)
-h shrinking: whether to use the shrinking heuristics, 0 or 1 (default 1)
-b probability_estimates: whether to train a SVC or SVR model for probability estimates, 0 or 1 (default 0)
-wi weight: set the parameter C of class i to weight*C, for C-SVC (default 1)
The k in the -g option means the number of attributes in the input data.
Et dans la vraie vie, alors ?
Concrètement, voici des exemples de ce que peut faire un SVM.
- Classer des fleurs suivant leur espèce, en fonction de la longueur et largeur de leurs pétales et sépales (c’est en fait un des datasets typiques du machine learning, appelé iris dataset) ;
- En médecine, les SVM sont utilisés pour reconnaître, par exemple, la diffusion dans le cerveau d’altérations liées aux AVC (en anglais);
- Reconnaissance de caractères sur des plaques d’immatriculation (en anglais);
- En médecine encore, identification des gènes responsables de certains types de cancer (en anglais);
- etc.
Comme nous en avions parlé, les SVM sont très efficaces quand le nombre de données d’entraînement est faible, en particulier en comparaison avec d’autres méthodes d’apprentissage automatique. Par exemple, les réseaux de neurones (outils d’apprentissage profond, oudeep learning, très à la mode) sont très performants, mais ont besoin d’une grosse quantité de données d’entraînement (quelques milliers à plusieurs millions voire plus, suivant la complexité du réseau de neurones). C’est donc par exemple dans le cas où le nombre de données d’entraînement est faible que l’on va favoriser les SVM aux réseaux de neurones.
Un SVM à la maison
Si vous voulez vous aussi jouer avec un SVM, vous pouvez bien sûr le coder vous-même, mais, à moins que vous n’adoriez résoudre algorithmiquement des problèmes d’optimisation quadratique, il vaut mieux utiliser une bibliothèque.
- En Python 2 et Python 3, vous pouvez vous servir de scikit, plus précisément de
sklearn.svm. - En Java, vous pouvez utiliser LIBSVM, qui a également été portée en Matlab, Python, Ruby, Perl, NodeJS, bindée en PHP…
- En Lua et en C, vous pouvez utiliser Torch, avec le module
torch-svm, etc.
Par ailleurs, je vous recommande la lecture de ce guide d’utilisation des SVM (en anglais), qui vous permettra d’éviter certains écueils, et donc d’améliorer la pertinence de votre SVM.
Pfiou !
Ca y est, vous savez comment fonctionne un SVM. Vous savez aussi comment les rendre plus performants grâce au kernel trick, et vous savez comment les adapter pour classer plus que deux catégories.
Il reste encore de nombreuses choses à apprendre sur les SVM : optimiser les paramètres du kernel choisi, utiliser les SVM pour faire de la régression, connaître la différence entre C-SVM et nu-SVM1, optimiser le calcul de , etc., mais je pense que vous en avez assez pour l’instant. Qui plus est, vous en savez bien assez pour voler de vos propres ailes, maintenant !
Merci à ache, backmachine, elegance, gbdivers, Holosmos, Hugo, SpaceFox, Vayel pour tous leurs retours pendant la période de bêta, qui fut très constructive. Merci également au gentil modo artragis. Merci enfin à Gabbro, pour tous ses retours pendant la validation du tutoriel, dont il s’est occupé.
Ici s’achève ce tutoriel. Bon machine learning à vous !
Sources, liens pour aller plus loin
Documents orientés théorie
- Support-Vector Network (en anglais) : un des articles fondateurs des SVM, par Cortes et Vapnik, de 1995.
- A Gentle Introduction to Support Vector Machines in Biomedicine (en anglais) : un document très détaillé et pédagogue.
- Machines à Vecteur Support, un document traitant d’autres aspects intéressants des SVM.
- Lagrange Multipliers Tutorial in the Context of Support Vector Machines (en anglais) : un document traitant de la résolution du problème d’optimisation quadratique des SVM.
- Support Vector Machines (en anglais) : un cours traitant des SVM de l’université de Stanford.
- History of SVMs (en anglais) : récit de l’invention des SVM, au fil des décennies.
- Machines à Vecteur de Support : l’article Wikipédia sur les SVM, histoire de faire dans l’originalité.
Documents orientés pratique
- A Practical Guide to Support Vector Classification (en anglais) : un mode d’emploi des SVM, qui détaille notamment les écueils classiques à éviter.
- Why use SVM? (en anglais) : un article comparant rapidement le SVM à d’autres algorithmes de machine learning.
- Kernel Functions for Machine Learning Applications (en anglais) : une large liste de fonctions noyaux, avec leurs caractéristiques.
- Pour faire bref, ce sont différentes méthodes pour autoriser les erreurs de classification, c.f. la partie « Cas non-séparable ».↩



 A quand un tuto détaillé sur le sujet ?
A quand un tuto détaillé sur le sujet ? 




