Tous droits réservés

Introduction aux codes correcteurs

Où l'on résoudra (presque) un problème fondamental en télécommunications

Comment transmettre efficacement un message binaire à travers un canal avec bruit ?

Derrière cette question barbare se pose un des problèmes fondamentaux que l'on rencontre dès lors qu'on s'intéresse à la communication entre ordinateurs (et donc, dès qu'on essaye de créer un réseau mondial, par exemple…). En effet, la transmission d'un message entre un émetteur et un récepteur est loin d'être chose aisée : dans la vie réelle, si vous criez quelque chose d'injurieux à votre voisin du dessus pour qu'il arrête de faire la fête à 3h du mat', il est peu probable qu'il comprenne votre invective à la lettre.

En informatique, c'est pareil : si vous envoyez un petit paquet de bits (ou d'octets, obscène individu que vous êtes) à l'autre bout du monde, il est peu probable que ceux-ci arrivent intacts ; ils auront sans doute été endommagés durant leur voyage chaotique à travers l'électronique qui vous sépare de votre cible. Pour ce qui est de votre voisin, il comprendra la teneur globale du message en jugeant par la quantité d'insultes et votre énervement intelligible. Pour ce qui est de votre ordinateur, il existe une théorie informatique qui permet de résoudre le problème : la théorie des codes correcteurs.

Première approche

Posons les choses

Commençons par établir un peu plus précisément le cadre du problème. Mettons que vous (oui, vous, derrière votre écran) désiriez envoyer un message à un ami, par des moyens informatiques ; il peut s'agir d'un simple courriel ou d'une transmission satellite, votre ami étant éventuellement un astronaute en mission. Dans tous les cas, votre message qui, après de multiples traitements, se résume à une série de bits — 01001110100110... — est susceptible d'être corrompu : n'importe lequel de ces bits peut être aléatoirement modifié au cours de la transmission.

Mettons que votre message soit envoyé sous la forme d'une onde de ce genre1 :

Signal NRZ transmis

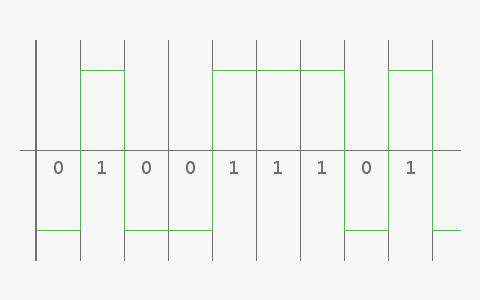
Les créneaux en vert transportent votre information, le seuil (le machin horizontal au milieu, là) permettant de différencier un 0 d'un 1. Une telle onde est malheureusement fragile, et de multiples causes (perturbation électromagnétiques aux alentours des câbles, orage solaire pour une transmission spatiale…) peuvent la dégrader pour donner quelque chose comme ça :

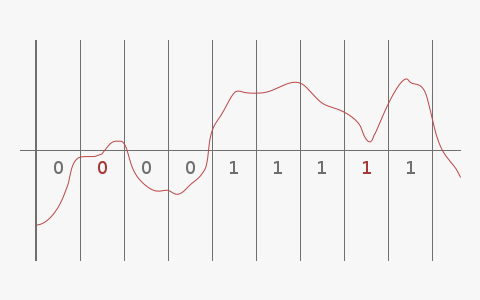
Signal NRZ altéré lors de la transmission

Et là, c'est le drame : l'onde ne ressemble plus à rien, au point que certaines parties aient changé de côté du seuil, altérant à la réception les bits qu'elles étaient censées transporter.

Si l'erreur est imprévisible, comment la corriger à la réception en n'utilisant pas plus de données que celles envoyées ? (Non, vous n'avez pas le droit de vous téléporter pour vérifier que le message a bien été reçu.) La seule solution est de surcharger le message initial, de lui faire porter une information supplémentaire qui servira à cette correction.

Bon, l'idée est bien belle, mais on voit difficilement comment l'exploiter au premier abord. C'est justement pour cela qu'existe toute la théorie des codes correcteurs, qui propose différents algorithmes et principes de surcharge permettant de détecter et de corriger des erreurs de transmission.

Notons la distinction entre détection d'une erreur, qui sera éventuellement suivie d'une demande de retransmission de la part du destinataire, et correction pure et simple d'une erreur à l'arrivée.

Voyons un peu comment on peut se débrouiller dans un premier temps avec des idées basiques.

Le bit de parité

Le bit de parité est probablement l'exemple le plus simple de code correcteur. Il suffisait d'y penser : en ajoutant à notre message un bit à la fin pour qu'il soit globalement de somme paire, le destinataire n'a plus qu'à calculer la somme de parité de ce qu'il reçoit pour déterminer s'il y a eu ou non une erreur.

Hein ? Somme de parité ?

Prenons pour exemple un message : 0110. Et bien, sa somme de parité vaut 0 + 1 + 1 + 0 = 2 (vous pouvez vérifier, j'ai compté de tête). On dira donc que ce message est pair ou de parité 0 ; pour notre exemple, on peut le coder en 01100 et on obtient bien un message codé pair. Envoyons alors ce message : si notre ami astronaute le reçoit tel quel, tant mieux ; s'il reçoit par exemple 01110, il obtiendra après calcul une somme de parité impaire valant 3, c'est-à-dire un message de parité 1, et saura qu'il y a anguille sous roche.

Simplissime ! Il suffit de se mettre d'accord pour savoir où se place le bit de parité dans le message codé, et comment demander de renvoyer un message, et hop, le tour est joué.

Mais…

Mais si c'était aussi simple, ce ne serait pas un domaine de recherche fondamental en informatique théorique. Deux problèmes subsistent en effet :

  • avec un simple bit de parité, impossible de détecter la position de l'erreur et donc de la corriger ; il faut obligatoirement demander un renvoi du message, ce qui n'est pas toujours facile et jamais optimal ;
  • de plus, regardez ce que donne une erreur double, par exemple sur les premier et troisième bits de notre message test : et oui, les doubles erreurs se compensent, et ça, c'est fichtrement problématique.

Le premier problème peut être en partie réglé en utilisant ce que l'on appelle un tableau de parité (pour faire simple, vous découpez votre message en tronçons que vous placez dans un tableau, vous appliquez un bit de parité à chaque ligne et colonne, et paf, ça fait un système de coordonnées2), mais le deuxième reste épineux. En fait, il est pour ainsi dire insoluble : vous ne pouvez pas être sûr que deux bits adjacents du message ne vont pas être corrompus simultanément, voire pire, tout votre message diaboliquement inversé… Difficile dans ces cas-là d'envisager une solution.

L'idée des codes correcteurs va alors être de trouver un compromis entre fiabilité et lourdeur, c'est-à-dire de tenter de corriger suffisamment d'erreurs pour assurer la transmission de manière satisfaisante (à vous de juger de ce qui est satisfaisant) tout en n'alourdissant pas exagérément le message de départ par un code complexe à mettre en œuvre ou à déchiffrer.

Et les codes de Hamming sont un bon pas vers ce compromis — plus efficace en tout cas que le bit de parité.

  1. Voir par ici pour plus de détails. ↩

  2. Si vous n'avez rien compris mais que vous êtes curieux, un cours très poussé sur les bits de parité et leurs dérivés est diponible ici. ↩

Les codes de Hamming

Un peu d'histoire

Richard Hamming est un grand mathématicien et informaticien du XXème siècle, dont les travaux lui ont entre autre valu de recevoir le prix Turing en 1968, pour son travail sur la théorie des codes, et notamment ce qui nous intéresse ici. Une médaille a même été créée en son nom, la médaille Richard Hamming, si ça c'est pas la classe.

Dans les années 40-50, Hamming travaillait sur des calculateurs à cartes perforées qui avaient le mauvais goût d'être peu fiables, c'est-à-dire de lire lesdites cartes avec difficulté. Il s'agit exactement d'un cas d'application des codes correcteurs : l'information transmise de l'homme à la machine, par le biais des cartes, était altérée de manière imprévisible.

Fort heureusement, la plupart du temps, les erreurs étaient suffisamment rares pour pouvoir être gérées en temps réel par les ingénieurs du labo. Mais durant les week-ends et autre jours fériés, les machines s'arrêtaient systématiquement sur des bugs ; c'est en voulant résoudre ce problème que Hamming créa les codes correcteurs qui portent son nom.

Mise en place du code de Hamming (7, 4, 3)

Idée générale

Les codes de Hamming sont une classe de codes, qui reposent sur le principe général mis au point par Richard (tu permets que je t'appelle Richard, Richard ?). Nous allons ici nous concentrer sur la mise en place du code (7, 4, 3) de cette classe : 7 comme la longueur du message une fois encodé, 4 comme la longueur du message initial, et 3 comme la distance de Hamming minimale de cette classe de codes1.

L'idée est d'obtenir, après décodage d'un message reçu, un syndrome, c'est-à-dire un nombre binaire donnant la position d'une erreur éventuelle (ou valant 0 si pas d'erreur). Vous l'aurez compris, on ne se préoccupera pas ici d'erreurs doubles, mais les codes de Hamming restent malgré tout très intéressants en ceci qu'ils permettent de détecter et de corriger des erreurs sur un message qui reste assez court.

Analyse du syndrome

Ici, notre message codé doit faire 7 bits de longueur, et l'initial 4 bits : le syndrome sera donc constitué des 3 bits restants. Analysons d'un peu plus près les positions que peuvent encoder les bits $abc$ d'un tel nombre :

$a$ $b$ $c$ Valeur du syndrome
0 0 0 0 (pas d'erreur)
0 0 1 1
0 1 0 2
0 1 1 3
1 0 0 4
1 0 1 5
1 1 0 6
1 1 1 7

Bon, déjà, notre hypothétique syndrome peut effectivement donner la position de n'importe quelle erreur dans le message à transmettre, ce qui est rassurant. Mais plus intéressant, on peut constater que chacun des bits $a$, $b$ et $c$ correspond à un groupe de 4 positions, respectivement (4, 5, 6, 7), (2, 3, 6, 7) et (1, 3, 5, 7). L'ensemble correspondant au bit $c$ est mis en gras dans le tableau.

C'est là que cela devient magique : considérons notre message à transmettre, $m_1m_2m_3m_4$ et plaçons-y nos bits de syndrome (que nous ne savons pas encore calculer), $cbm_1am_2m_3m_4$. Au passage, le placement des bits du syndrome se fait en toute logique aux seuls endroits où les groupes ne se chevauchent pas, pour éviter par la suite toute ambiguïté dans le code.

Le retour du bit de parité

Nos bits de syndrome deviennent alors ni plus ni moins que les bits de parité de leurs groupes attitrés.

Je m'explique : si à la réception du message, le destinataire calcule la parité de chacun des groupes (celui de $a$, celui de $b$ et celui de $c$) et trouve 0 dans les trois cas, cela signifie que les trois groupes auront été transmis intacts, et donc le message entier avec eux. Si à l'inverse, il trouve une valeur non nulle, le chevauchement des groupes est tel que la valeur trouvée correspondra exactement à la position de l'erreur commise.

Prenez un peu le temps de comprendre comment ça marche, comme je le disais, c'est un peu magique. Mais ça marche ; la preuve par l'exemple : notre bon vieux 0110 s'encode en cb0a110 soit, en calculant les bits de parité, 1100110. Supposons que le destinataire reçoive 1100010, alors le calcul des parités lui donnera :

  • pour le bit $a$, correspondant au groupe (4, 5, 6, 7) : 0 + 0 + 1 + 0 = 1, le groupe est de parité 1 ;
  • pour le bit $b$, correspondant au groupe (2, 3, 6, 7) : 1 + 0 + 1 + 0 = 2, le groupe est de parité 0 ;
  • pour le bit $c$, correspondant au groupe (1, 3, 5, 7) : 1 + 0 + 0 + 0 = 1, le groupe est de parité 1.

Soit un syndrome de 101, c'est-à-dire 5 en décimal, la position effective de l'erreur. Bien joué, Richard.

Apparté : soyons fous, faisons des maths

Il est intéressant de noter à titre de curiosité, que la théorie des codes correcteurs peut tirer bon parti des préceptes de l'algèbre. En effet, un message, suite de quatre bits, n'est ni plus ni moins qu'un vecteur de $F_2^k$ (avec $k=4$ chez nous) vu comme $F_2$-espace vectoriel, où $F_2 = \{0, 1\}$ est un corps fini fort sympathique. Un message codé est alors un vecteur de $F_2^{k'}$ (avec cette fois $k'=7$ ici), et le code est finalement une application linéaire (et heureusement injective) entre ces deux espaces.

S'ensuivent tout un tas de décompositions matricielles qui permettent de formaliser les calculs de messages codés et de syndromes, et tout cela est d'autant plus pertinent que l'algèbre fournit un cadre mathématique confortable pour étudier la plupart des codes correcteurs existants (autres que celui de Hamming) et pour théoriser dessus. Or, le mathématicien sait bien que rien ne vaut un cadre formel confortable, et après tout, on est ici à la croisée des mathématiques et de l'informatique.

  1. C'est complètement hors du cadre de ce cours, mais très intéressant ; ça parle de topologie de l'espace message et de choses dans ce goût-là, et si ça vous botte, je vous encourage à vous documenter sur la question. Wikipédia fournit une très bonne base. ↩

Le théorème de Shannon

Il existe bien d'autres codes correcteurs que ceux de Hamming, et Internet regorge d'information si le sujet vous intéresse ; vous pouvez par exemple vous interroger sur le fait que les codes de Hamming soient parfaits, ou aller voir du côté des codes cycliques.

Mais je vous propose maintenant d'aborder une question plus abstraite : quelles sont les limites de la théorie ? Jusqu'où peut-on aller en termes de correction d'erreurs ? Avec quelle efficacité ? Une inégalité démontrée par Claude Shannon fournit quelques éléments de réponse à ces questions.

Avis aux allergiques, cette dernière partie contiendra beaucoup un peu de maths ; si vous y êtes réfractaires, essayez de vous extraire de la masse de symboles pour comprendre les idées sous-jacentes, je tenterai de vous y aider.

Enoncé du théorème

Pour un code correcteur, notons $M$ la longueur d'un message initial, $M_c$ sa longueur une fois codé et $q$ la probabilité d'erreur sur chacun des bits au cours de la transmission. Alors,

$$\frac MM_c \leqslant 1 - \left(q.log_2\frac 1q + (1-q).log_2\frac 1{1-q}\right)$$

Voilà, donc, partie suivante...

Je plaisante. Tentons de voir ce qui se cache derrière cette formule barbare ! Pour cela, nous allons devoir définir la redondance, notion dont nous aurions pu parler plus tôt : il s'agit du rapport $M_c/M$. Pour exemple, dans le cas du code de Hamming vu plus haut, elle vaut 1,75 ; évidemment, on voudrait qu'elle soit aussi proche de 1 que possible pour un code le plus "léger" possible.

Ce que Shannon nous donne, c'est un lien direct entre la redondance (ou plutôt son inverse, si vous avez suivi) et la probabilité d'une erreur sur un bit du message. Il nous dit que pour gérer n'importe quelle probabilité d'erreur, la redondance de code nécessaire sera toujours plus grande que (ou son inverse plus petit que, suivez toujours) cette formule compliquée à droite de l'inégalité. En d'autres termes, pour une certaine probabilité d'erreur, cela ne sert à rien de s'acharner à optimiser notre code au-delà d'une certaine limite.

Toujours pas ? Voyons sur quelques valeurs. Si chacun des bits a une chance sur quatre d'être corrompu (ce qui est énorme), la formule en $q$ nous donne la valeur de 5,3 : un code qui corrige autant d'erreurs qu'on veut sur un message transmis dans ces conditions, aura toujours une redondance supérieure à 5,3. Autrement dit, pour corriger un maximum d'erreur ayant chacune une probabilité d'occurrence de 1/4, inutile de se fatiguer à encoder notre message avec moins de 5,3 bits de code par bit de message initial, c'est voué à l'échec. Pour une probabilité d'erreur d'un dixième, cette valeur limite est de 1,9 ; pour un millième, elle tombe à 1,012.

Notons tout de même que cette limite théorique est loin d'être atteinte avec nos connaissances actuelles. Par exemple, dans le cas des transmissions spatiales vers des sondes en transit, où un $q = 1/4$ est monnaie courante, les codes utilisés en pratique ont plutôt une redondance de l'ordre de 250 que de 5,3…

Mais le résultat le plus marquant que présente Shannon, c'est qu'il s'agit là d'un théorème d'existence : il existe un code de redondance limite (telle que donnée par l'inégalité) qui corrige effectivement autant d'erreurs que l'on veut pour la probabilité correspondante ! Méditez là-dessus, cela vaut son pesant de cacahuètes. Malheureusement, si un tel code existe, Shannon ne nous dit pas comment l'obtenir, ce serait trop facile1…

Une démonstration

Vous avez avalé le gros théorème ci-dessus ? Vous voulez le digérer ? Parfait, passons à sa démonstration !

Ou plutôt, une démonstration approximative et (un peu) intuitive, proposée par Richard Feynmann2 (décidément, les Richard sont à l'honneur dans ce cours) ; une démonstration plus rigoureuse s'appuierait sur des concepts beaucoup plus poussés tels que la théorie de l'information, qui n'ont pas leur place ici.

Remarquons tout d'abord que pour n'importe quel code, la longueur d'un message une fois codé est forcément supérieure à la somme des longueurs du message initial, et des bits qui donnent la position de l'erreur (dans le cas des codes de Hamming, il y a égalité mais c'est rare) : en conservant les notations précédentes et en notant $m$ le nombre de bits de syndrome,

$$M_c \geqslant m + M$$
On obtient donc en mettant à la puissance de 2
$$2^{M_c-M} \geqslant 2^m$$
or $2^m$, c'est précisément le nombre de positions différentes pour une erreur que nos bits de code peuvent signaler. Pour qu'un code fonctionne, ce nombre doit être égal au nombre de possibilités de répartition des erreurs dans le message, après transmission ; nombre que l'on peut approximer (les statisticiens me pardonneront ce grossier à-peu-près de physicien) par
$$\begin{pmatrix} M_c \\ q.M_c \end{pmatrix} = \dfrac {M_c!}{(q.M_c)!(M_c-q.M_c)!}$$
En utilisant (avec les mains et à son grand dam) l'équivalent de Stirling, on obtient rapidement quelque chose comme
$$M_c - M \geqslant M_c.log_2M_c - (M_c - q.M_c).log_2(M_c-q.M_c) - q.M_c.log_2(q.M_c)$$
ce qui après quelques manipulations donne l'inégalité de Shannon. Ouf.

Cette démonstration, outre sa relative simplicité, propose quelques idées intéressantes et permet de visualiser un peu le comportement des codes correcteurs ; le théorème lui-même étant un résultat puissant et très élégant, j'espère que vous parviendrez à vous en rendre compte !

  1. Il est en fait possible de s'approcher de la limite de Shannon, en utilisant des schémas de codage aléatoire et en laissant varier la redondance ; mais là encore, cela va au-delà du cadre de ce cours. ↩

  2. Dans ses Leçons sur l'informatique, une compilation de notes de cours parue en 2006. Un excellent ouvrage, ce type était un génie, un pédagogue hors pair et il avait de l'humour, en plus. ↩

Ce cours n'a pu vous fournir qu'une approche superficielle, quoi qu'assez éclectique, du vaste domaine que sont les codes correcteurs. Il s'appuie majoritairement sur le contenu de l'ouvrage de Feynman mentionné plus haut, ainsi que sur une flopée de pages Wikipédia, l'encyclopédie libre étant assez bien pourvue en la matière.

Une piste pour aller plus loin, outre la quantité de documentation que vous pourrez trouver en ligne, serait d'implémenter votre propre algorithme exécutant un code de Hamming par exemple. Je l'ai fait en Python, et avec un peu d'astuce j'ai même réussi à vérifier empiriquement le théorème de Shannon… Si le cœur vous en dit, voilà un défi informatique intéressant !

N'hésitez pas à me contacter par MP si vous avez une question ou une remarque relative à ce cours. Dans tous les cas, j'espère que sa lecture vous aura été aussi agréable qu'a été pour moi sa rédaction. L'informatique théorique recèle bon nombre de domaines relativement abordables et aussi intéressants que celui-ci ; soyez curieux, et ce monde s'offrira à vous…

:)

23 commentaires

Comme j'ai aussi quelques bases (qui vont jusqu'au décodeur de viterbi) dans ce domaine, je peux te dire que c'est plutôt réussi.

Par contre, personnellement, j'ai du mal, dans les démonstrations mathématiques avec les phrases du style :

Naturellement, il vient donc

Ca me fait toujours penser au prof de math qui veut montrer sa supériorité en qualifiant des passages de "triviaux" etc. Le site s'adresse surtout au débutant, et ça, ça fait jamais plaisir de se prendre une phrase comme ça dans la tronche.

En effet, un message n'est ni plus ni moins qu'un vecteur de (avec chez nous) vu comme -espace vectoriel, où est un corps fini fort sympathique

là tu me fais penser à mon prof de math génial qui utilise les mêmes expressions que toi ^^.

Par contre, je pense qu'une petite phrase qui nous explique pourquoi on peut utiliser ces notations ça serait cool, non?

+0 -0

Merci pour le compliment !

Désolé pour les formulations dans la démo, c'est une déformation qui vient de l'habitude d'en rédiger de manière rigoureuse… Il est vrai que sur un site pour débutants, c'est un peu limite. De toute façon, j'ai déjà quelques corrections minimes à apporter ; après un peu plus de retours, je regrouperai et referai valider le tout. :)

J'ai aussi eu un prof de maths génial qui ponctuait ses explications de ce genre de commentaires j'ai dû prendre ça de lui… Mais c'est intentionnellement que je n'ai pas plus développé cette partie. Mathématiquement, c'est très intéressant, mais impossible à réellement vulgariser sans réexpliquer la base des espaces vectoriels, et j'ai pas vraiment la place pour ça. ^^ Je verrai éventuellement pour détailler un brin le passage, sans aller beaucoup plus loin.

+0 -0

Je verrai éventuellement pour détailler un brin le passage, sans aller beaucoup plus loin.

je pense qu'en deux phrase tu peux avoir tout expliqué:

  • un mot c'est un ensemble de deux symbole pris dans l'ensemble {0, 1}
  • cet ensemble possède deux propriétés : l'addition est un ou exclusif, la multiplication par un mot tel que 10, 100 ou 1000 est un décallage vers la gauche de autant de 0.
+0 -0

Prenez un peu le temps de comprendre comment ça marche, comme je le disais, c'est un peu magique. Mais ça marche ; la preuve par l'exemple : notre bon vieux 0110 s'encode en cb0a110 soit, en calculant les bits de parité, 1100110. Supposons que le destinataire reçoive 1100010, alors le calcul des parités vous donnera un syndrome de 101, c'est-à-dire 5 en décimal, la position effective de l'erreur

je dois avouer que je suis un peu perdu surtout que je ne connaissais pas ce domaine… mais même en calculant le 1+1+0+0+0+1+0 =3 donc impair comment arrives tu au 101 ? je pense que je vais relire tout ça à tête reposé car ça doit être "évident" mais là je passe à côté du coup

pour le reste j'ai réussi à suivre, même les passages mathématique :p

+0 -0

@Asvin : 101, c'est le syndrome obtenu en calculant les parités des groupes qui sont définis juste avant : on reçoit 1100010. Pour le bit $a$ qui code les positions (4, 5, 6, 7)1, ça donne 04+05+16+07=1, c'est impair, on note 1 ; pour $b$, on trouve 12+03+16+07=2, c'est pair, on note 0 ; et pour $c$ on trouve de nouveau un résultat impair donc 1. Finalement le syndrome $abc$ vaut bien 101, c'est-à-dire 5 en décimal !

Il s'agit du même concept que les bits de parité, mais appliqué sur différents groupes de bits du message qui se croisent de manière (très) judicieuse. Effectivement, si tu relis ça à tête reposée ça te paraîtra sans doute plus clair. :)

@artragis : c'est pas faux, mais c'est pas mathématique (enfin pas au sens où l'utilisation des espaces vectoriels s'avère intéressante). Me faudrait réfléchir à un autre moyen de voir ça.

  1. Damned, une coquille dans le cours. Ajoutée à la liste des corrections ! ↩

+0 -0

Il existe une figure de mnémotechnique pour les bits de hamminh (4,7) : Tu prends tes 4 bits initiaux et tu en fais une étoile avec le troisième au centre. Puis tu place les trois bits de hamming dans les espaces restant. chaque bit de hamming sera la somme des bits initiaux qui lui sont voisins dans l'étoile.

mnémotechnique pour hamming

+0 -0

Ouep, dans mon travail initial qui a donné naissance à ce cours, j'avais fait un schéma de ce genre avec des patates. Merci pour l'image, ça donne une visualisation complémentaire intéressante. :)

(Attention tout de même : quand tu dis "la somme", c'est la somme modulo 2, que j'appelle la somme de parité dans le cours ; je précise à tout hasard.)

+0 -0

Bravo pour ce mini tuto. un domaine qui m'intéressait et j'ai enfin l'occasion de me pencher sur le sujet.

+0 -0

Salut, j'ai tenté d'implémenter quelques fonctions en Haskell, que voici:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
import Data.List

hamming_error_emplacement (c:(b:(m1:(a:(m2:(m3:(m4:[]))))))) = binToDec (((a+m2+m3+m4) - (div (a+m2+m3+m4) 2)*(a+m2+m3+m4)):((((b+m1+m3+m4) - (div (b+m1+m3+m4) 2)*(b+m1+m3+m4))):(((c+m1+m2+m4) - (div (c+m1+m2+m4) 2)*(c+m1+m2+m4)):[])))
    where binToDec l = sum $ map (2^) $ findIndices (==1) $ reverse l

hamming_generator (m1:(m2:(m3:(m4:[])))) = ((m2+m1+m4)-(div (m2+m1+m4) 2)*(m2+m1+m4)):(((m1+m3+m4)-(div (m1+m3+m4) 2)*(m1+m3+m4)):(m1:(((m2+m3+m4)-(div (m2+m3+m4) 2)*(m2+m3+m4)):(m2:(m3:(m4:[])))))) 

hamming_fix_message s@(c:(b:(m1:(a:(m2:(m3:(m4:[]))))))) = loop s (hamming_error_emplacement s)
    where loop s@(x:xs) emplacement = if emplacement <= 0 then s
        else if s!!(emplacement-1) == 0 then let s2 = (replaceNth (emplacement-1) 1 s) in loop s2 (hamming_error_emplacement s2) else let s2 = (replaceNth (emplacement-1) 0 s) in loop s2 (hamming_error_emplacement s2)

replaceNth n newVal (x:xs)
     | n == 0 = newVal:xs
     | otherwise = x:replaceNth (n-1) newVal xs

Cependant, je me pose une question : combien d'erreur peut corriger le code de Hamming ? Merci d'avance :)

+0 -0

le nombre d'erreur maximal que l'on peut corriger automatiquement est $n_e = \frac{(d-1)}{2}$

Le message complet est composé du message effectif et de la redondance apportée par le code. S'il y a des erreurs partout, on ne peut pas corriger.

Il faut aussi bien comprendre que les codes présentés dans cet articles sont des codes simples qui ne permettent pas d'encodages efficaces de gros paquets de données.

Souvent quand tu fais de la vidéo, tu vas utiliser les codes polynomiaux ou continus avec comme nec plus ultra le codage/décodage de Viterbi.

+0 -0

mind blown Ma réaction au code de hamming.

Seule mini-critique que je ferais c'est que c'est pas vraiment clair ce que sont a, b, et c tout de suite. Tu dis qu'ils sont respectivement la parité des groupes (4, 5, 6, 7), (2, 3, 6, 7), et (1, 3, 5, 7), sans préciser qu'on omet le premier élément du groupe quand on ""créée" a,b et c (sans quoi on peut arriver à un paradoxe). J'ai buggué un moment là dessus, mais bon après je suis pas très futé non plus…

Super intéressant en tout cas ça donne envie de creuser tout ça !

+0 -0

Hello, Il faudrait corriger un petit bug : le tag sécurité est mis pour cet article hors les codes correcteurs n'amènent aucune sécurité puisqu'il est très facile de les mettre en jour si on modifie intentionnellement les informations.

La sécurité c'est un triptique : confidentialité/autenticité, intégrité, accessibilité. Les codes correcteurs permettent de renforcer l'intégrité. C'est donc une forme de sécurité.

+0 -0

J’ai lu cette partie dans le livre "Réseaux" des éditions Pearson et j’ai voulu compléter par quelques explications supplémentaires sur les limites et les possibilités. Merci d’avoir apporté ce petit plus sur le théorème de Shannon.

Cela dit, j’ai mieux compris le détails dans le livre car il indique que les bits de parité se retrouve sur les bits correspondant à 2^n . (Soit, de gauche à droite, sur un code(11,7) (4 bits de parités), sur les bits 1,2,4 et 8. Les autres sont des bits de message (3,5,6,7,9,10,11). Ainsi, il devient facile d’expliquer le calcul. Seule chose "tricky" : il faut inverser les bits du syndrome pour obtenir la position du bit en erreur.

Merci tout de même de ton article qui est vachement bon !!!

+0 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte