Au cours de votre apprentissage, vous avez peut-être déjà vu des nombres écrits sous une forme étrange, constituée d’un petit nombre, éventuellement avec plein de décimales, multiplié par une puissance de 10 :
Cette manière d’écrire les nombres s’appelle la notation scientifique. Elle facilite le travail des scientifiques et ingénieurs en donnant les informations essentielles en un coup d’œil. Savoir s’en servir est indispensable, car on la retrouve partout dès qu’il s’agit de sciences et techniques.
Ce tutoriel vise à vous apprendre l’essentiel sur cette notion incontournable qu’est la notation scientifique des nombres.
Ce tutoriel aborde les notions suivantes :
- définition de la notation scientifique (générale, cas particuliers, écritures alternatives) ;
- utilisation des nombres en notation scientifique (compacité, ordres de grandeur et chiffres significatifs, comparaisons) ;
- manipulation des nombres en notation scientifique (écriture d’un nombre en notation scientifique, calcul avec les nombres en notation scientifique) ;
- bonus : notations voisines (notation ingénieur, notation scientifique binaire).
Ce tutoriel nécessite les prérequis suivants :
- calcul élémentaire (addition, soustraction, multiplication, division) ;
- comparaison de nombres (plus petit, plus grand, …) ;
- manipulation des puissances (notamment les puissances de 10).
- Reconnaître la notation scientifique
- Utiliser la notation scientifique
- Manipuler la notation scientifique
- Bonus : notation ingénieur et notation scientifique binaire
Reconnaître la notation scientifique
Définition
Sans plus attendre, voici la définition-phare de notre tutoriel.
Un nombre est écrit en notation scientifique s’il est écrit sous la forme suivante :
où :
- est le signe du nombre ( si le nombre est positif, s’il est négatif) ;
- est un nombre compris entre 1 (inclus) et 10 (exclu), appelé significande ;
- est un entier relatif (c’est-à-dire positif ou négatif) appelé exposant.
Pour faire simple, un nombre en notation scientifique est un nombre écrit sous une forme standardisée, où l’on distingue son signe, sa « valeur » (le significande), et sa « taille » (l’exposant).
Vérifier qu’un nombre est en notation scientifique, c’est s’assurer que le nombre est sous la forme , et surtout que est bien entre 1 inclus et 10 exclu et est bien un entier relatif.
Vous rencontrerez régulièrement des notations scientifiques écrites un peu différemment de la forme usuelle, mais qui restent des nombres écrits en notation scientifique. Les variantes d’écriture les plus courantes sont les suivantes.
- Usage d’un point multiplicatif à la place du signe « multiplier » usuel. Exemple : .
- Notation « calculatrice » avec le point décimal et la lettre « E » ou « e » pour indiquer l’exposant. Exemples :
5.1E5,5.1e5.
Vous voilà prévenus, ne soyez pas déroutés si vous rencontrez ces formes-là !
Exemples
Observez les nombres suivants, écrits sous la forme . À chaque fois le significande est bien entre 1 et 10 et l’exposant est entier : il s’agit donc bien de nombre en notation scientifique.
Observez maintenant les nombres suivants, écrits également sous la forme , mais qui ne sont pas en notation scientifique. Soyez attentif à pourquoi ils ne sont pas en notation scientifique, même si la forme semble correcte au premier abord.
- n’est pas une notation scientifique car est supérieur à .
- n’est pas une notation scientifique car n’est pas un entier.
- n’est pas une notation scientifique car est inférieur à .
Cas particuliers
Le cas du zéro
Avec la définition ci-dessus, on ne peut pas écrire zéro en notation scientifique ! En effet, zéro est inférieur à un, de sorte qu’il ne peut pas constituer le significande et il n’est pas non plus possible d’ajuster l’exposant pour faire zéro. Pour zéro, on écrit alors tout simplement « 0 ».
En vérité, il est assez rare d’avoir une quantité parfaitement nulle en sciences, et il est ainsi peu courant d’obtenir zéro comme résultat d’un calcul et de devoir l’écrire en notation scientifique !
Le cas des nombres compris entre 1 et 10
Prenons par exemple le nombre . En toute rigueur, ce nombre n’est pas une notation scientifique et il faudrait écrire à la place . Cependant, pour des raisons de lisibilité et de brièveté (et de paresse), on se permet d’écrire tout simplement . Toute l’information nécessaire est là, sans superflu.
Exercice
Pour les nombres suivants, dites s’ils sont en notation scientifique ou non, et pourquoi.
La solution est ci-dessous.
- Pas en notation scientifique. Justification : est supérieur ou égal à .
- En notation scientifique. Justification : est bien entre 1 (inclus) et 10 (exclu) et est bien un entier relatif.
- Pas en notation scientifique. Justification : n’est pas un entier.
- Pas en notation scientifique. Justification : est strictement inférieur à .
- En notation scientifique. Justification : est bien entre 1 (inclus) et 10 (exclu) et est bien un entier relatif.
Utiliser la notation scientifique
Vous savez maintenant reconnaître la notation scientifique, mais à quoi peut-elle bien servir ? Nous verrons dans cette section différents cas de figure où la notation scientifique sait se rendre très utile. Les cas décrits ici ne forment évidemment pas une liste exhaustive, mais donnent un aperçu de situations courantes !
Écrire un nombre de manière compacte
La notation scientifique est utile pour écrire des nombres de manière compacte et lisible. Sans la notation scientifique, certains nombres ont tendance à prendre des proportions démesurées et il est alors difficile de les appréhender facilement.
Prenons l’exemple de la masse d’un atome d’uranium, exprimée en kilogrammes (symbole kg). Avec la notation scientifique, on écrit :
Avec la notation décimale usuelle, on aurait dû écrire la chose suivante, beaucoup plus longue et moins lisible :
Je ne sais pas vous, mais quand je regarde la fin du nombre, je n’arrive pas à regarder le début en même temps : ce n’est pas lisible. On peut également voir le même désagrément pour les nombres très grands. Le nombre suivant est la masse de la Terre en kilogrammes :
Sans la notation scientifique, on devrait écrire la chose suivante. Regardez tous les zéros qui s’enchaînent ; même en groupant les nombres, la lecture est difficile !
Déterminer un ordre de grandeur et identifier les chiffres significatifs
Un des avantages majeur de la notation scientifique est de donner l’ordre de grandeur d’un nombre et ses chiffres significatifs en un coup d’œil.
Ordre de grandeur
L’ordre de grandeur d’un nombre est la puissance de 10 la plus proche. Quand un nombre est écrit en notation scientifique, il est très simple de le trouver avec les règles suivantes1 :
- si le significande est strictement inférieur à 5, alors l’ordre de grandeur est , où est l’exposant ;
- si le significande est supérieur ou égal à 5, alors l’ordre de grandeur est , où est toujours l’exposant.
Prenons encore la masse de l’atome d’uranium : . Le significande vaut et est donc inférieur strictement à 5. L’ordre de grandeur de cette masse est donc de kilogrammes.
Prenons notre deuxième exemple, la masse de la Terre : . Le significande vaut et est donc supérieur ou égal à 5. L’ordre de grandeur de cette masse est donc (car 25 est égal à 24 + 1).
La facilité de détermination de l’ordre de grandeur permet aussi de vérifier la cohérence d’un résultat. Si vous calculez la distance de la Terre à la Lune et que vous trouver un ordre de grandeur de 102 m (c’est-à-dire une centaine de mètres), alors vous savez tout de suite qu’il y a un gros problème dans vos calculs, puisque l’ordre de grandeur attendu est de l’ordre de 108 m (plusieurs centaines de milliers de kilomètres).
Chiffres significatifs
Les chiffres significatifs d’un nombre sont les chiffres dont on est certain, plus un dernier chiffre sur lequel pèse une incertitude. Par exemple, pour le nombre 1254, les chiffres certains sont 1, 2 et 5 et le dernier chiffre est 4, qui est incertain (il pourrait s’agir de 3 ou de 5 en l’absence d’indication sur l’incertitude).
En notation décimale, en particulier pour les grands nombres, il est impossible de voir les chiffres significatifs en un coup d’œil, puisqu’il peut y avoir de nombreux zéros non significatifs, qui sont là pour donner l’ordre de grandeur. Donner les chiffres significatifs dans cette notation nécessite des annotations spécifiques peu pratiques. Ce problème se manifeste, par exemple, quand on écrit la masse de la Terre en notation décimale : .
Au contraire, en notation scientifique, il est facile de déterminer les chiffres significatifs, puisque tous les chiffres visibles le sont. En particulier, s’il y a des zéros à la fin du significande, alors ils sont significatifs. Quand on écrit la masse de la Terre, par exemple, il suffit de lire les chiffres : .
Exercice
Donner l’ordre de grandeur et les chiffres significatifs pour chacun des nombres suivants, écrits en notation scientifique.
La solution est ci-dessous.
- : les chiffres significatifs sont 3 et 8, l’ordre de grandeur est .
- : les chiffres significatifs sont 9 et 3, l’ordre de grandeur est .
- : les chiffres significatifs sont 1, 8 et 1, l’ordre de grandeur est .
Comparer des nombres en un clin d’œil
Règles de comparaison
Grâce à l’exposant et au significande, il est extrêmement rapide de comparer des nombres écrits en notation scientifique. Les règles de comparaison sont les suivantes :
- si les deux nombres ont des exposants différents, alors le nombre avec l’exposant le plus grand est le nombre le plus grand ;
- si les deux nombres ont le même exposant, alors le nombre avec le significande le plus grand est le nombre le plus grand.
La comparaison des exposants est aisée, puisqu’il s’agit d’entier relatifs. La comparaison des significandes reste toujours facile puisqu’on a affaire à des nombres compris entre 1 inclus et 10 exclu, qu’on compare en un coup d’œil.
Exercice
Comparez les nombres pour chacun des couples de nombres suivants écrits en notation scientifique.
- et
- et
- et
La solution est ci-dessous.
- Les règles données ici pour déterminer l’ordre de grandeur sont une simplification. La définition exacte complique un peu les choses, donc ne vous inquiétez pas si vous ne saisissez pas tout. En toute rigueur, l’ordre de grandeur d’un nombre correspond à la puissance de 10 la plus proche sur une échelle logarithmique. Concrètement, cela signifie que la séparation ne se fait pas sur le nombre 5, comme expliqué ci-avant, mais . Cela est dû au fait que sur une échelle logarithmique, le milieu est obtenu en effectuant une moyenne géométrique des deux puissances de 10 qui encadrent directement le nombre considéré (ce qui donne ) et non pas une moyenne arithmétique (ce qui donne ).↩
Manipuler la notation scientifique
Maintenant que vous savez reconnaître et utiliser l’écriture scientifique, il est temps d’apprendre à la manipuler.
Écriture d’un nombre en notation scientifique
La chose la plus fondamentale est de savoir comment écrire un nombre en notation scientifique étant donné son écriture décimale, afin de pouvoir exploiter la notation scientifique pour n’importe quel nombre que vous croiserez.
Méthode
Pour écrire un nombre en notation scientifique, il « suffit » de trouver le significande et l’exposant, le signe étant évident. Pour cela, je propose la méthode suivante.
- Si le nombre est plus petit que 1, multiplier le nombre par 10 autant de fois que nécessaire pour qu’il soit compris entre 1 (inclus) et 10 (exclu). Si le nombre est plus grand que 1, procéder de même, mais en divisant par 10. Vous obtenez ainsi le significande.
- Compter le nombre de fois que vous avez multiplié ou divisé par 10. Cela vous donne la valeur de l’exposant. Le signe de l’exposant est positif si vous avez divisé et négatif si vous avez multiplié.
- Utiliser le significande et l’exposant pour écrire votre nombre en notation scientifique.
Faisons ensemble un exemple. Supposons que nous voulions écrire 0,0000326 en notation scientifique. Je procède ainsi.
- Le nombre est plus petit que 1, donc je vais multiplier par 10 jusqu’à ce que le résultat soit entre 1 inclus et 10 exclu. J’obtiens 3,26, qui est donc mon significande.
- Pour ce faire, j’ai multiplié 5 fois par 10. Mon exposant aura donc pour valeur 5 et comme j’ai dû multiplier, il s’agira de -5.
- La notation scientifique de 0,0000326 est donc .
Comme multiplier par 10 revient à décaler la virgule d’un chiffre vers la droite et diviser par 10 revient à décaler la virgule d’un chiffre vers la gauche, il est possible de procéder de la manière suivante, plus visuelle, mais équivalente.
- Décaler vers la gauche ou la droite la virgule, de sorte à ce que le nombre obtenu soit entre 1 (inclus) et 10 (exclu). Le nombre obtenu est le significande.
- Compter le nombre de fois que vous avez décalé la virgule, cela donne la valeur de l’exposant. Le signe de l’exposant est positif si vous avez décalé vers la gauche et négatif si vous avez décalé vers la droite.
- Utiliser le significande et l’exposant pour écrire votre nombre en notation scientifique.
Pourquoi ces méthodes marchent ? Il s’agit en fait de manipulation de puissances. Si on multiplie et divise un nombre par 10, on ne change pas sa valeur. Il en résulte que l’on peut faire ça successivement et trouver ainsi la notation scientifique du nombre :
Exercice
Mettez en notation scientifique les nombres suivants.
La solution est ci-dessous.
- . Il est également possible de le laisser tel quel pour plus de lisibilité (voir cas particuliers dans la première section).
- . Cas particulier, on laisse tel quel.
Calcul avec les nombres en notation scientifique
La notation scientifique se révèle très utile pour les calculs, car elle permet de les réaliser plus facilement, y compris sans calculatrice.
Multiplications et divisions
Les multiplications et divisions sont aisées grâce aux propriétés des puissances de 10.
On peut suivre le mode opératoire suivant pour réaliser un calcul impliquant des multiplications et des divisions.
- Simplifier toutes les puissances de 10, pour qu’il n’en reste plus qu’une (au numérateur idéalement).
- Faire les opérations liant les différents significandes et mettre le résultat en notation scientifique.
- Simplifier la puissance de 10 calculée à l’étape 1 avec le résultat obtenu à l’étape 2.
Prenons un exemple. On souhaite calculer :
On simplifie les puissances de 10, et on obtient :
On calcule le terme de gauche, qui vaut environ et on le met sous forme scientifique :
On simplifie pour obtenir le résultat final :
Additions ou soustractions
Les additions et soustractions sont aussi simples, mais demandent un peu plus d’attention.
Quand on souhaite additionner deux nombres en notation scientifique, la première étape est de les mettre au même exposant. On choisit le plus grand des deux, car c’est souvent celui qui va rester dans le résultat final. Ensuite, on effectue le calcul normalement et on remet sous forme scientifique.
Prenons un exemple. On souhaite calculer l’addition suivante :
On met au même exposant :
On calcule l’addition avec les significandes qui sont de petits nombres :
Comme le résultat de l’addition des significandes est bien entre 1 inclus et 10 exclu, le nombre est déjà sous forme scientifique. Si le nombre avait été supérieur ou égal à 10 ou strictement inférieur à 1, il aurait fallu travailler un peu plus pour remettre en notation scientifique.
Bonus : notation ingénieur et notation scientifique binaire
Notation scientifique binaire
La notation scientifique marche très bien avec la base 10, qu’on utilise habituellement. Mais qu’est-ce qu’il se passe quand on écrit en base 2, comme c’est très souvent le cas en informatique ? Eh bien, on utilise la notation scientifique binaire !
Un nombre écrit en notation scientifique binaire est un nombre écrit sous la forme suivante :
où :
- est le signe, positif ou négatif ;
- est le significande, compris entre 1 inclus et 2 exclu ;
- est l’exposant, un entier relatif.
Le significande, encore une fois, se situe dans un intervalle particulier. Pour la notation scientifique décimale, il était entre 1 et 10 ; ici, il est entre 1 et 2. On voit donc que la base forme toujours la borne supérieure de l’intervalle.
Cette notation scientifique binaire a les mêmes propriétés très pratiques que la notation scientifique usuelle, mais adaptées pour les nombres binaires. Par exemple, en binaire, décaler la virgule vers la gauche revient à diviser par deux et donc à diminuer l’exposant de 1.
Notation ingénieur
La notation ingénieur est une notation voisine de la notation scientifique. Bien que moins répandue que la notation scientifique, elle est souvent proposée, sur les calculatrices notamment.
Un nombre en notation ingénieur est un nombre écrit sous la forme :
où :
- est le signe du nombre, positif ou négatif ;
- est le significande, compris entre 1 inclus et 1000 exclu ;
- est l’exposant, un entier relatif multiple de 3.
On voit tout de suite le lien de parenté avec la notation scientifique classique. La différence vient du fait qu’on utilise seulement les puissances de 10 dont l’exposant est multiple de 3, comme 10-9, 10-6, 10-3, 103, 106, 109 etc. L’intervalle pour le significande s’accorde avec cela : il peut prendre des valeurs entre 1 inclus et 1000 exclu. En quelque sorte, la notation ingénieur est une notation scientifique en base 1000 !
L’utilité de cette notation est qu’elle est très proche des unités de mesures usuelles (millimètre, mètres, kilomètre par exemple) et qu’elle facilite éventuellement la conversion.
Ce tutoriel touche à sa fin. Vous savez désormais l’essentiel sur la notation scientifique, qui n’a plus de secrets pour vous.
Je remercie @bendia, @Blackline et @etherpin pour les retours pendant la rédaction, ainsi que @adri1 pour le processus de validation.
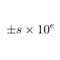

 Les exercices complètent très bien le tutoriel !
Les exercices complètent très bien le tutoriel !
