Le rôle principal des lignes électriques est de transporter l’électricité entre les zones de production et les zones de consommation. Cependant, transporter l’électricité entre un point A et un point B n’est pas aussi facile que transporter un colis, car il faut prendre en compte les lois des circuits électriques pour parvenir à ses fins ! Notamment, il passe par un pilotage de la tension des générateurs présents sur le réseau afin que la puissance circule là où on a besoin d’elle.
Dans ce tutoriel, nous étudions un modèle simplifié des lignes électriques qui illustre bien les grands principes appliqués pour piloter les réseaux électriques réels. Bien que simple, le modèle reste relativement représentatif, et surtout, il permet de comprendre l’essentiel de ce qu’il se passe avec seulement des notions élémentaires en électricité (loi des mailles, loi d’Ohm notamment).
Modélisons une ligne électrique
Producteurs et consommateurs
Pour simplifier, on adopte une modélisation en courant continu, et pas en courant continu alternatif, comme c’est le cas en général sur les réseaux électriques.
Les producteurs peuvent être des machines électriques dans les centrales, des panneaux solaires, des batteries, et j’en passe. Les consommateurs sont également très divers : moteurs électriques, éclairage, équipements électroniques par exemple. Dans les deux cas, ils ont pour caractéristique essentielle de produire ou de consommer de la puissance, parce que c’est ce dont ils ont besoin pour remplir leur fonction. Notre modélisation devrait être capable de prendre ça en compte.
La plupart des gros générateurs sur les réseaux électriques (centrales au gaz par exemple), sont capables d’imposer leur tension de sortie au réseau électrique. Du point de vue de la modélisation, cela signifie qu’ils se comportent comme des sources de tension.
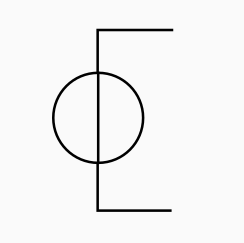
Les consommateurs fonctionnent de diverses manières. On pourrait se dire qu’un consommateur, c’est comme une simple résistance qui consomme de la puissance. Cependant, ce n’est pas une très bonne idée, parce que la puissance consommée par une résistance dépend de la tension à laquelle elle est soumise. Or, beaucoup de consommateurs fonctionnent à puissance constante : si la tension d’entrée diminue, ils vont avoir tendance à consommer plus de courant pour compenser. Du point de vue du réseau électrique, mettre une résistance n’est donc pas forcément une bonne solution.
On pourrait imaginer des choses compliquées avec des résistances variables en fonction de la tension pour résoudre le problème. Mais en vérité, il n’y a pas besoin de tout ça ! En effet, du point de vue du réseau électrique, un groupe de consommateurs et producteurs se comporte comme un seul fournisseur ou consommateur (selon le signe de la puissance), avec une tension régulée grâce aux générateurs présents dans le groupe. En images, cela donne :
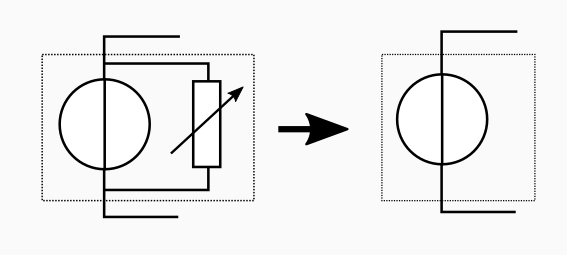
Notre problème s’en trouve simplifié : les consommateurs et les producteurs sont modélisés identiquement. Seule la puissance nous dira si une source de tension se comporte comme un générateur ou un consommateur du point de vue du réseau.
Lignes électriques
Les lignes électriques réelles sont relativement complexes d’un point de vue électrique. Encore une fois, on les simplifie en faisant le choix d’un modèle à courant continu.
Pour faire au plus simple, on pourrait se dire qu’un câble, ce n’est rien (résistance nulle). Malheureusement, cela ne marche pas, car mettre deux générateurs de tension en parallèle n’est pas autorisé.1
La solution à ce problème, tout en gardant un modèle simple, est de modéliser la ligne électrique par une simple résistance.
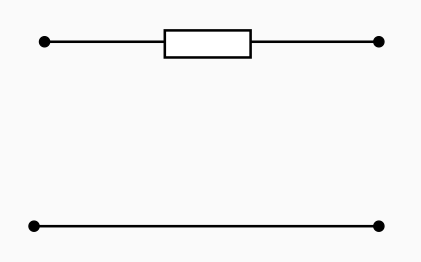
On pourrait diviser la résistance entre le haut et le bas, mais électriquement c’est la même chose ; il n’y a donc pas d’avantage à le faire.
- C’est un peu comme la division par zéro en mathématique. Ça ne marche juste pas du tout.↩
Pilotons une ligne électrique
Notre réseau constitué d’une ligne électrique reliant deux zones correspond au circuit électrique suivant :
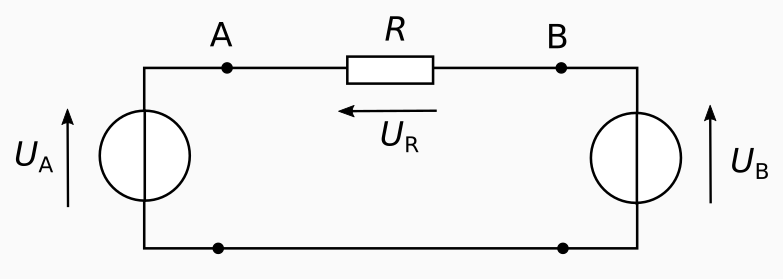
Il y a trois puissances que l’on peut définir :
- la puissance produite (ou consommée) par le nœud A, ;
- la puissance produite (ou consommée) par le nœud B, ;
- la puissance dissipée par le câble, .
En général, les puissances et sont connues à l’aide de prévisions faites par l’opérateur du réseau : on sait où sont les centrales et leurs capacités maximales ainsi que les consommations approximatives.
Ce qui nous intéresse ici est la puissance échangée sur la ligne, puisqu’il faudra la transférer. Elle n’apparaît pas directement dans nos trois puissances, mais peut être assimilée à ou . En effet, pour que le réseau fonctionne suffisamment bien, la puissance dissipée par le câble doit être faible. Grossièrement, la puissance échangée est donc approximativement celle produite d’un côté et consommée de l’autre.
Le signe de et indiquera si la puissance s’écoule de A vers B ou inversement. Si est positive et négative, cela signifie que la puissance s’écoule du nœud A vers le nœud B. Inversement, si est positive et est négative, la puissance s’écoule de B vers A.
J’ai dit en introduction que les tensions jouent un rôle dans cet échange de puissance ce que nous allons voir tout de suite.
Calcul
Faisons quelques calculs sur le schéma électrique vu précédemment afin de comprendre le rôle des tensions en A et en B.
On applique tout d’abord la loi des mailles dans la seule maille du circuit, ce qui permet d’écrire :
En appliquant la loi d’Ohm, on remplace par son expression en fonction du courant :
Maintenant, on peut exprimer le courant en fonction de la différence de tension et de R :
Autrement dit, si est plus grande que , le courant circule de A vers B dans la résistance, et dans le sens inverse dans le cas contraire. Cette expression du courant nous servira à calculer les puissances.
Regardons donc les puissances. J’utilise ici la convention récepteur pour toutes les expressions. Cela signifie que si l’expression de la puissance est positive, cela correspond à une puissance consommée. (Pour en savoir plus sur les conventions, je vous renvoie à mon tutoriel sur le sujet.)
Déjà, une observation rassurante : le signe des deux puissances est opposé ! On aura donc bien un producteur d’un côté et un consommateur de l’autre.
On remplace le courant par l’expression trouvée précédemment :
On a donc le comportement suivant : si est plus grande que , est négative, donc c’est une puissance effectivement générée (on est en convention récepteur), et la puissance circule effectivement de A vers B. Si l’on a la comparaison inverse entre les tensions, la puissance circulera dans la direction opposée.
En résumé : dans ce modèle, il suffit de monter un peu la tension d’un côté par rapport à l’autre pour lui envoyer de la puissance !
Application
Décidons que l’on produit 100 MW à gauche et qu’on consomme 100 MW à droite. Il faut donc transmettre 100 MW (plus quelques pertes).
En ordre de grandeur, les tensions sont de l’ordre de la centaine de kilovolts. Pour simplifier, disons qu’elles sont d’environ 100 kV. Les deux tensions sont proches.
Sur un réseau de transport, la résistance dépend de la distance à parcourir mais reste faible, disons dans notre cas 1 ohm :
Du coup, quelles sont les tensions exactes à appliquer pour avoir tel que voulu ? On peut choisir librement certaines variables, car les équations offrent un peu de liberté mathématique :
On peut utiliser l’expression de pour aboutir à :
En faisant le calcul :
La tension à gauche est supérieure d’un pour cent à celle à droite et permet de faire circuler des dizaines de mégawatts ! Cet ordre de grandeur correspond à ce qu’on peut avoir sur des réseaux réels.
La puissance perdue dans la ligne électrique dans cet exemple est de l’ordre de 1 mégawatt, ce qui est modeste et correspond bien à l’ordre de grandeur des pertes (quelques pour cent) dans les réseaux électriques haute tension de bonne qualité tels qu’on peut les trouver dans les pays européens.
Dans ce modèle simplifié, vous avez vu qu’on peut décider de faire circuler de la puissance sur une ligne électrique en ajustant la tension à ses extrémités, ce qui n’a rien de sorcier quand la plupart des générateurs sont capables de piloter leur tension de sortie !
Le monde réel est un peu plus compliqué : le courant est alternatif, les réseaux sont maillés. Pourtant, les principes restent similaires. On pilote alors les générateurs avec leurs niveaux de tension et leurs déphasages, et la circulation dans le réseau maillé peut également être contrôlée, moins facilement toutefois que dans notre exemple simplifié.