Un ordinateur, ça chauffe !
Je sais que j'enfonce une porte ouverte : les chercheurs en architecture des ordinateurs ont d'ailleurs déjà beaucoup travaillé sur le sujet. La consommation énergétique d'un ordinateur a différentes causes, liées au fonctionnement des transistors. Mais au-delà de ces considérations techniques, y a-t-il une limite à la quantité de chaleur que peut dégager un ordinateur ?
Un ordinateur est avant tout un gros bloc de matière, et est donc soumis aux lois de la physique : ce sont ces lois qui posent des limites à la consommation d'énergie d'un ordinateur. Les lois de ce qu'on appelle la thermodynamique vont ainsi jouer de sales tours aux concepteurs de processeurs. Les lois de la thermodynamique permettent de décrire à haut niveau la quantité d'énergie utile que l'on peut tirer du fonctionnement d'un système physique, et quelle est la part d'énergie gaspillée en chaleur. À partir de ces lois, on peut poser une limite à la consommation d'énergie d'un ordinateur normal : cette limite s'appelle la limite de Landauer.
Dans ce qui va suivre, nous allons voir d'où sort cette limite, et surtout : comment concevoir une architecture matérielle qui permette de contourner cette limite ! Pour commencer, nous allons faire une petite introduction toute mignonne sur les notions de thermodynamique qui nous seront utiles, et allons aborder la notion d'entropie.
- Une histoire d'énergie, mais pas que !
- La quantité de chaleur minimale d'une écriture
- Calcul réversible
Une histoire d'énergie, mais pas que !
Si on prend un machin quelconque (notre ordinateur, par exemple), celui-ci possède une certaine quantité d'énergie, que l'on appelle l'énergie interne. Cette énergie peut prendre plusieurs formes : de l'énergie chimique, mécanique, cinétique, nucléaire, électrique, etc.
Énergie interne et chaleur
La thermodynamique nous dit qu'il existe une forme d'énergie qui correspond intuitivement à la chaleur d'un objet : l'énergie thermique. Il faut de l’énergie pour chauffer un objet, peut importe que la source de l'énergie soit des réactions chimiques, des processus mécaniques, ou autre : de l'énergie, sous n'importe quelle forme, peut se transformer en énergie thermique. L'inverse est aussi vrai : on peut transformer de la chaleur en une autre forme d'énergie nommée travail : pensez aux locomotives à vapeur qui transformaient la chaleur de la vapeur en mouvement.
Dans toutes ces transformations entre différentes formes d'énergie, l’énergie totale est conservée : de l'énergie peut se transformer d'une forme à une autre, mais toute création ou destruction d'énergie est impossible. Pour paraphraser, on peut dire que toute variation de l'énergie interne d'un objet est égale à la quantité d'énergie entrante, moins la quantité d'énergie sortante. C'est la première loi de la thermodynamique. Si on crée de la chaleur, cela signifie donc qu'une portion de l'énergie interne de l'ordinateur a été transformée en chaleur via une transformation.
Macro-états
Lors de son fonctionnement, l'ordinateur, comme tout système physique, va changer d'état, et de l'énergie va se transformer en permanence : des bits vont changer d'états, des atomes vont changer de place, de la chaleur va être crée, etc. Extérieurement, on peut voir certaines grandeurs physiques varier : la température augmente, par exemple. Et ce n'est pas spécifique à un ordinateur : tout objet physique peut subir des transformations de ses propriétés externes. Ces transformations vont faire varier certaines propriétés de l'objet considéré :
- sa température va varier (l'ordinateur chauffe, par exemple) ;
- sa pression peut augmenter (cas d'un gaz qu'on chauffe) ;
- son volume aussi (idem) ;
- sa composition chimique peut varier ;
- etc.
L'ensemble de ces grandeurs à grande échelle forme ce que l'on appelle le macro-état d'un système, qui est défini par la température, la pression, le volume et la composition chimique et la masse. Un système peut passer d'un macro-état à un autre via diverses transformations. Certaines de ces transformations vont transformer de l'énergie non-thermique en énergie thermique et vice-versa : la température du système peut augmenter ou diminuer, comme dans le cas d'un ordinateur en fonctionnement.
Transformations réversibles et irréversibles
Certaines de ces transformations d'énergie ont la particularité d'être inversibles : il existe un moyen pour revenir exactement à l'état initial en repassant par tous les états rencontrés lors de la transformation. En clair, on peut repasser le film à l'envers sans aucun problème pour revenir à la situation de départ. Lorsqu'on rembobine le film, on gagne autant d'énergie dans la transformation qu'on en dépense pour revenir à l'état initial : la chaleur créée lors de la transformation peut être récupérée et être transformée en une autre forme d'énergie.
Cependant, une transformation d'énergie n'est pas toujours inversible : il se peut qu'on ne puisse pas toujours revenir exactement à l'état initial sans perdre plus d'énergie qu'on en a utilisé pour la transformation. Par exemple, essayez de dissoudre un morceau de sucre dans de l'eau : croyez-vous que l'on puisse revenir exactement à l'état initial, pour retrouver la morceau de sucre à l'identique, à l'atome prêt, sans dépenser d'énergie ? Quand une transformation non-inversible a lieu, un peu d'énergie est définitivement transformée en chaleur.
Entropie
D'où vient cette perte d'énergie lors d'une transformation irréversible ? Pour comprendre le phénomène, les physiciens ont dû introduire une grandeur physique que l'on nomme l'entropie. En première approche, celle-ci permet de déterminer si une transformation est possible sans apport d'énergie extérieure.
Le second principe de la thermodynamique nous dit que cette entropie ne se conserve pas : on peut en créer facilement, mais pas en détruire. Si on diminue l'entropie d'une entité, c'est que de l'entropie a été déplacée en-dehors de l'entité. Dit autrement, une entité isolée, c'est à dire qui n'échange pas d'énergie avec l'extérieur, voit son entropie augmenter ou rester constante : son entropie ne peut pas diminuer.
Il est impossible de créer de l'entropie lors d'une transformation réversible : de l'entropie peut être échangée avec l'extérieur, mais celle-ci peut revenir à sa place en inversant la transformation. Par contre, toute transformation irréversible va créer de l'entropie. Cette augmentation d'entropie fait que l'énergie utile diminue : de l'énergie se transforme en énergie thermique, énergie thermique qui ne peut pas être récupérée sans faire varier la température du machin en question. C'est de là que provient la perte de chaleur dans un ordinateur : les calculs qu'il fait ne sont pas réversibles, et vont donc créer de l'entropie.
Le point de vue à grande échelle
En supposant la température constante et une transformation réversible, l'entropie peut être définie pour une transformation réversible:
- Q est la quantité d'énergie thermique contenue par le système (sa variation représente un transfert de chaleur) ;
- T est la température ;
- S est l'entropie.
Vu qu'il s'agit d'une réaction réversible, cette entropie est échangée avec l'extérieur de l'objet : lors d'une réaction réversible, l'entropie globale (entité et extérieur compris) reste constante.
Le point de vue microscopique
D'un point de vue physique, l'entropie d'un objet dépend uniquement de sa structure interne. N'importe quel machin est toujours constitué d'un ensemble de particules élémentaires, de champs énergétiques (électriques, gravitationnels, etc). Ces particules et champs peuvent s'agencer de diverses façons en fonction des contraintes extérieures. Par exemple, les atomes d'un liquide peuvent se répartir d'un très grand nombre de façons dans l'espace, sans compter que les vitesses des atomes sont plus ou moins dispersées dans un intervalle bien précis.
Un macro-état peut être satisfait par un grand nombre de configurations possibles : à composition chimique, température, pression, et volume donné, les atomes pourront se répartir de diverses manières. Chaque configuration s'appelle un micro-état. Pour faire simple, un micro-état est une description totale du système observé, description qui ne peut pas être plus complète : il s'agit de toute l'information disponible sur le système, une fois le macro-état de celui-ci fixé. Dit autrement, un objet peut passer d'un micro-état à un autre sans pour autant changer de macro-état. L'entropie peut être définie en fonction de la probabilité d'observer chaque micro-état lors d'une mesure donnée. Si on note cette probabilité $p_{i}$, alors l'entropie vaut :
$k_B$ est une constante, nommée la constante de Boltzmann. Ce coefficient $k_B$ est un coefficient qui sert à donner une unité à l'entropie : celle d'une énergie divisée par une température.
La quantité de chaleur minimale d'une écriture
Grâce aux formules du dessus, on peut calculer la chaleur minimale dégagée par le changement d'entropie d'un système. On peut donc calculer la chaleur minimale obtenue lors de l'écriture d'un bit en comparant l'entropie d'un bit avant et après son écriture.
Comparaison d'entropie avant et après écriture d'un bit
Du point de vue de la théorie de l'information, un bit est un symbole qui peut prendre deux valeurs équiprobables : 0 et 1. Dit autrement, un bit est une entité qui ne possède que deux micro-états équiprobables. L'entropie d'un de ces micro-état est donc égale à :
Vu qu'il en a deux (0 et 1), la formule nous donne :
Si on modifie ce bit, on le fait passer avec certitude à l'état 0 ou 1. Après modification, ce bit est dans un état bien précis qui est connu : c'est soit 0, soit 1, avec une probabilité de 1. L'incertitude étant nulle, l'entropie du bit est donc nulle elle aussi. La différence d'entropie entre un bit avant et après écriture est donc égale à :
Limite de Landauer
En multipliant cette entropie par la température, on en déduit quelle est la la quantité de chaleur minimale dépensée pour modifier un bit de manière irréversible. Il suffit simplement d'appliquer la formule $\Delta(Q) = T \times \Delta(S)$, en remplaçant le $\Delta(S)$ par la valeur que l'on vient de calculer. On obtient la limite de Landauer, la quantité de chaleur minimale que produit un calcul sur un bit.
De nombreux travaux ont cherché à vérifier la véracité de cette limite, et les observations expérimentales actuelles vont toutes dans le sens de l’hypothèse de Landauer. Mais quelques travaux théoriques semblent remettre cette limite en question, même s'ils n'ont pas donné lieu à des observations en laboratoire : la limite de Landauer tient toujours.
Pour le moment, les ordinateurs actuels ont une consommation énergétique par modification de bit qui est largement supérieure à la limite de Landauer : la différence est d'un facteur 1000, voir plus. Il faut dire qu'une grande partie de la consommation énergétique provient du fait que les circuits d'un ordinateur ne sont pas supraconducteurs : la résistance électrique des interconnexions et les condensateurs cachés dans les transistors fait que de l’énergie se transforme irrémédiablement en chaleur d'une manière apparemment décorrélée de la limite de Landauer. Ceci dit, cela n’empêche pas de regarder vers l'avenir, et de prévoir ce qui se passera une fois que l'on aura atteint cette limite de Landauer.
Calcul réversible
La seule solution pour contourner cette limite est de faire en sorte que les calculs effectués soient totalement réversibles. À chaque étape du calcul, on doit pouvoir revenir à l'étape précédente à partir du résultat ! Pour cela, il faut créer des architectures matérielles qui permettent ce genre de calcul réversible. Et les portes logiques actuelles ne permettent pas cela. Prenons par exemple une simple porte logique ET : impossible de retrouver les deux bits de départ à partir du bit de résultat. Et le problème se pose aussi avec le XOR, le NAND, et toutes les portes logiques du même acabit. La raison est simple : pour retrouver l'original à partir du résultat, il faut que l'opération soit une bijection. Et qui dit bijection dit autant de sorties que d'entrées.
Portes réversibles
Pour passer outre ce problème, les chercheurs en architecture des ordinateurs ont inventés de nouvelles portes logiques qui sont réversibles, et forment une bijection entre le résultat et les opérandes. Ces nouvelles portes logiques ont donc autant d'entrées que de sorties : certaines de ces sorties sont utiles, tandis que d'autres sont bonnes pour la poubelle et ne servent qu'à rendre le calcul réversible. Il suffit de relier ces portes logiques réversibles entre elles pour obtenir un circuit réversible.
Les portes réversibles les plus connues sont :
- la porte de Toffoli ;
- la porte de Fredkin.
Porte de Toffoli
La porte de Toffoli est une porte à :
- trois entrées $e_0$, $e_1$, et $e_2$ ;
- et trois sorties $s_0$, $s_1$, et $s_2$.
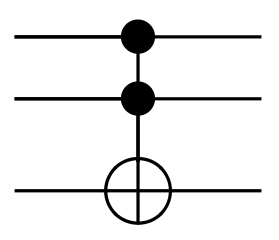
Son fonctionnement est simple :
- quand $e_0$ et $e_1$ sont tous les deux à 1, la sortie $s_2$ est égale à l'inverse de l'entrée $e_2$ ;
- dans le cas contraire, la sortie $s_2$ est égale à l'entrée $e_2$.
| $e_0$ | $e_1$ | $e_2$ | $s_0$ | $s_1$ | $s_2$ | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 0 | 1 | |
| 1 | 1 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 0 |
On se retrouve alors avec :
- $s_2 = e_2 \oplus (e_1 . e_0)$ ;
- $s_1 = e_1$ ;
- $s_0 = e_0$.
Porte de Fredkin
La porte de Fredkin est aussi une porte à trois entrées et trois sorties.
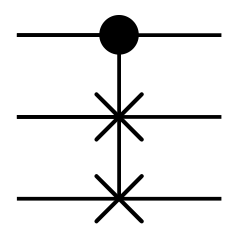
Son fonctionnement est simple :
- l'entrée $e_0$ est recopiée sur la sortie $s_0$ ;
- quand l'entrée $e_0$ est à 1, elle échange les deux autres entrées ;
- dans le cas contraire, elle recopie les deux autres entrées sur les sorties adéquates.
| $e_0$ | $e_1$ | $e_2$ | $s_0$ | $s_1$ | $s_2$ | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 |
On se retrouve alors avec :
- $s_2 = (e_2 . \overline{e_0}) \oplus (e_1 . e_0)$ ;
- $s_1 = (e_1 . \overline{e_0}) \oplus (e_2 . e_0)$ ;
- $s_0 = e_0$.
Problèmes
Cependant, il y a un problème pour l'approche du calcul réversible : il faut repasser le calcul à l'envers pour récupérer l'énergie dépensée. Et cela signifie refaire passer les portes logiques utilisées par les macro-états qu'elles ont traversé lors du calcul. Cela pose quelques contraintes :
- les entrées doivent devenir des sorties (et vice-versa) et doivent refaire le calculs à l'envers ;
- sans compter qu'elles doivent le faire en repassant par touts les états traversés lors du calcul initial : l'évolution de la température lors du retour-arrière doit être strictement inverse à celle obtenue lors du calcul.
Les portes logiques actuelles ne permettent pas ce genre de fantaisies et la solution proviendra sans doute de circuits supraconducteurs spécialisés. Par exemple, des physiciens travaillent à l'heure actuelle pour créer des portes réversibles avec ce qu'on appelle des jonctions Josephson, des espèces de condensateurs aux armatures supraconductrices.
Les architectures réversibles sont prometteuses, mais il y a loin de la coupe aux lèvres. Il faudra certainement plusieurs années de recherche, peut-être même plusieurs décennies, avant d'avoir des architectures réversibles réellement utilisables. En attendant, nous devrons nous contenter des améliorations d'efficacité énergétique de nos processeurs. Il reste encore de la marge pour diminuer la consommation des processeurs et des autres composants et la recherche à ce sujet est encore en cours. Mais rien ne nous empêche de penser à l'après-demain.


 )
)
