Nous sommes nombreux à avoir un jour voulu faire de jolis tableaux de variations ou de signes, pour accompagner une étude de fonction, par exemple. Et force est de constater que ce n’est pas si simple que ça. Nous pouvons utiliser les tableaux classiques, mais le résultat n’est pas très esthétique et, surtout, on passe beaucoup plus de temps à faire le tableau en lui-même qu’à le remplir.
En effet, l’écriture d’un tableau complexe n’est pas simple en LaTeX et est assez lourde. Ceci explique bien pourquoi il peut être fastidieux d’utiliser les packages array ou encore tabular pour faire ces tableaux. De plus, même en négligeant cela, la création des flèches pour un tableau de variations reste compliquée.
C’est pourquoi il existe des packages pour nous permettre de faire des tableaux plus facilement. C’est l’utilisation d’un de ces packages, Tkz-Tab que nous allons aborder dans ce tutoriel.
Prérequis
Connaissance des bases du LaTeX (un tutoriel est disponible ici).
Objectifs
Découvrir un moyen simple de composer esthétiquement des tableaux de signes et de variations en LaTeX.
- TikZ, un package qui en a dans le ventre
- Tableaux de signes
- Tableaux de variations
- Compléter nos tableaux
- Personnalisation
TikZ, un package qui en a dans le ventre
Pour faire nos tableaux, nous pourrions utiliser la commande \array. Mais ce ne serait pas très efficace. Nous allons, comme nous l’avons déjà dit, utiliser un package adapté : le package Tkz-Tab.
TikZ et Tkz-Tab
Nous allons commencer par parler du package TikZ. Il s’agit d’un package créé vers 2006 et qui jouit d’une grande popularité. Il permet d’inclure des figures et illustrations dans nos documents sans avoir à sortir de l’environnement LaTeX, c’est-à-dire sans inclure d’images extérieures, mais bien en « décrivant » directement ce que nous souhaitons obtenir dans notre fichier source. Voici un code source qui permet de dessiner un carré.
\begin{tikzpicture}
\draw (0, 0) -- (5, 0); % AB = 5
\draw (5, 0) -- (5, 5); % BC = 5
\draw (5, 5) -- (0, 5); % CD = 5
\draw (0, 5) -- (0, 0); % CD = 5
\end{tikzpicture}
Voici ce qu’on fait ici :
- on relie le point A(0, 0) au point B(5, 0) ;
- on relie le point B(5, 0) au point C(5, 5) ;
- on relie le point C(5, 5) au point D(0, 5) ;
- on relie le point D(0, 5) au point A(0, 0).
Tout ceci dans un environnement tikzpicture, qui est l’élément de base de ce package. On peut l’assimiler à une figure et chacun d’eux correspond à un dessin.
Mais pourquoi parle-t-on de ce package ? Nous on veut faire des tableaux, non ?
En fait, le package Tkz-Tab qui nous permettra de dessiner nos tableaux dépend de TikZ. Mais il ne faut pas s’inquiéter, aucune connaissance de TikZ n’est requise pour utiliser Tkz-Tab. Nous devons juste savoir qu’on dessine dans l’environnement tikzpicture (et c’est justement ce que nous venons de voir). Puisque Tkz-Tab dépend de TikZ, il faut également inclure ce dernier. Heureusement, Tkz-Tab charge TikZ et nous pouvons donc utiliser cette ligne.
\usepackage{tkz-tab}
TikZ peut être en conflit avec d’autres packages, le plus notable étant le conflit avec xcolor, qu’il faudra inclure avant TikZ.
Les premiers tableaux
Nous avons dit que tikzpicture était le principal environnement du package TikZ. C’est le seul qu’il nous faut connaître. La commande principale du package Tkz-Tab est \tkzTabinit et sert à initialiser un tableau. Cette commande doit être placée dans un environnement tkzpicture. Elle a pour arguments obligatoires deux listes dont les éléments sont séparés par des virgules :
- la première liste correspond à des paires (les éléments des lignes de notre tableau (typiquement une variable et son image par une fonction) et la taille de la ligne qui leur est associée (en centimètres) de la forme
{$x$ /1 , $f(x)$ /1}; - la deuxième liste correspond aux antécédents que nous voulons afficher (donc aux colonnes que l’on obtiendra dans la seconde partie du tableau) de la forme
{$0$, $6$, $+\infty$}.
Avec les deux listes précédentes et donc avec la commande…
\begin{tikzpicture}
\tkzTabInit{$x$ / 1 , $f(x)$ / 1}{$0$, $6$, $+\infty$}
\end{tikzpicture}
… on obtient ce tableau.
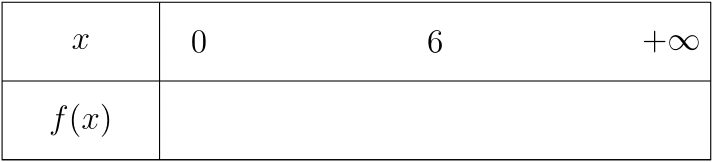
Maintenant que nous avons vu la commande \tkzTabInit, nous savons faire des tableaux à n lignes (il suffit de passer comme premier argument une liste de n éléments) de hauteurs différentes.
Nous pouvons également utiliser la commande \tikz à la place de l’environnement \tikzpicture. Dans ce cas, nous devons placer un point-virgule là où nous refermions l’environnement.
Tableau minimum
Les deux arguments de la commande tkzTabInit sont obligatoires comme nous l’avons vu, donc pour pouvoir faire des tableaux vides, il nous faut des arguments minimums :
- le premier argument minimum est
{ / 1}ce qui correspond à aucun élément affiché, dans une ligne dont on doit quand même donner la hauteur ; - le second argument comprend deux éléments minimums, qui correspondent aux bornes de l’intervalle. Le second argument minimum est donc
{ , }, ce qui correspond bien à deux éléments (en fait deux vides).
Finalement le code minimal est celui-ci.
\tkzTabInit{ / 1}{ , }
Principe des tableaux
Le principe de Tkz-Tab est de créer le tableau ligne par ligne après l’avoir initialisé. Avec l’initialisation, nous créons un tableau vide de n lignes (seuls les antécédents et les « noms » des différentes lignes sont définis), puis nous disposons de commandes pour remplir ces lignes, donc faire nos tableaux de signes, de valeurs et de variations. Bien sûr, si nous initialisons un tableau avec n lignes, nous ne pouvons pas définir ensuite n + 1 lignes. La syntaxe générale est donc la suivante.
\begin{tikzpicture}
\tkzTabInit{}{}
% commande pour la ligne 1
% commande pour la ligne 2
% ...
% commande pour la ligne n
\end{tikzpicture}
Puisque le séparateur utilisé dans les listes est la virgule, nous ne pouvons pas l’utiliser directement. Il nous faudra soit placer le texte entre accolades, soit utiliser une commande d’affichage (typiquement \numprint) pour ne pas avoir d’erreur.
Tableaux de signes
La commande magique
Nous voici enfin prêts à commencer des tableaux de signes. La commande permettant de faire une ligne de signes est \tkzTabLine (on aurait pu s’en douter), et elle prend comme argument obligatoire une liste d’éléments séparés par des virgules, tout comme la commande \tkzTabInit.
Ces éléments correspondent à ce qu’il faudra afficher dans notre ligne. Si nous avons antécédents, cette liste comprendra 2n - 1 éléments (n éléments placés en dessous des antécédents et n - 1 éléments placés entre deux antécédents).
Généralement, les éléments pairs correspondent aux signes (ou à une « zone interdite » de la fonction) alors que ceux impairs correspondent à des traits (traits avec un zéro, double barre…).
Voici les paramètres que nous devrons passer pour produire ces différents symboles :
dplace une double barre centrée ;tplace un trait en pointillé centré ;zplace un zéro centré sur un trait un pointillé ;hpermet de définir une zone interdite (la zone est hachurée par défaut) ;+place un signe + ;-place un signe -.
Néanmoins, nous pouvons passer quasiment n’importe quoi en paramètre (toujours en faisant attention aux virgules), même du texte.
Le premier tableau de signes
Nous allons reprendre le tableau de la première partie et le compléter un peu.
\begin{tikzpicture}
\tkzTabInit{$x$ / 1 , $f(x)$ / 1}{$0$, $6$, $8$, $+\infty$}
\tkzTabLine{z, -, d, h, d, +, }
\end{tikzpicture}
On obtient ce tableau.

Nous n’avons pas utilisé toutes les options disponibles, mais nous aurions pu le faire, et essayer le t, par exemple.
Il nous faut remarquer que nous n’avons rien mis au niveau de +\infty, mais que nous avons quand même placé une dernière virgule dans le code. Dès lors, nous devrions être capable de trouver le tableau minimal.
\tkzTabLine{, , , , , , }
Eh oui, tout comme précédemment, il suffit de mettre le nombre de virgules nécessaires (si nous avons n antécédent, il faut 2n - 2 virgules).
Et encore
Comme nous l’avons déjà dit, nous pouvons passer n’importe quel symbole ou presque en paramètre à \tkzTabLine. En particulier, cela nous permet de faire des tableaux dans lesquels nous écrirons du texte (grâce à la commande \text du package amsmath), ou encore des expressions mathématiques. Par exemple, nous pouvons écrire le tableau de variations d’une fonction affine (de la forme ax + b, avec a et b deux constantes).
\begin{tikzpicture}
\tkzTabInit{$x$ / 1 , $ax + b$ / 1}{$-\infty$, $-\dfrac{b}{a}$, $+\infty$}
\tkzTabLine{, \text{signe de } a, z, \text{signe de } -a, }
\end{tikzpicture}
Qui donne…
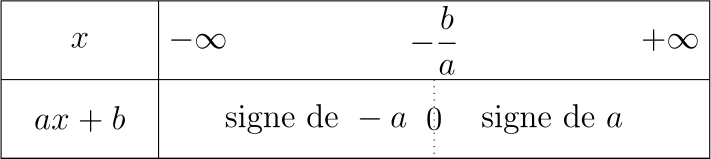
On peut également faire le tableau très simple de la valeur absolue.
\newcommand{\abs}[1]{\left\lvert#1\right\rvert} % Commande pour obtenir la valeur absolue.
\begin{tikzpicture}
\tkzTabInit{$x$ / 1 , $\abs{x}$ / 1}{$-\infty$, $0$, $+\infty$}
\tkzTabLine{, -x, z, x, }
\end{tikzpicture}
On obtient…

Tableaux de variations
\tkzTabVar
Tout comme nous avons \tkztabLine pour faire des lignes de signes, nous avons \tkzTabVar pour faire des lignes de variations et, là encore, elle prend en paramètre une liste dont les éléments sont séparés par une virgule (encore et toujours une liste).
Ces éléments sont des groupes d’expressions qui correspondent à ce qui sera affiché sous nos antécédents. Si nous avons n antécédents, cette liste comprendra donc n groupes.
Ces expressions sont de la forme s / x. x correspond à l’expression qui sera affiché, et s à la manière dont il sera affiché dans le tableau et à son emplacement vertical. s contient des signes plus et moins. En fait, on peut distinguer deux types de groupes.
- Ceux avec un seul signe dans
spermettent de placer une unique expression en antécédent. L’expression sera alors bien de la formes / x. - Ceux avec deux signes permettent de placer deux expressions en antécédent. C’est le cas typique d’une fonction qui n’est pas définie (ou pas continue) en un point et dont la limite à gauche et à droite est différente. L’expression devient alors
s / g / d, avecgl’expression qui sera affichée à gauche etdcelle qui sera affichée à droite.
En fait, le signe permet d’indiquer la position de l’antécédent dans le tableau. Il est placé en haut si le signe est plus et en bas si le signe est moins. Cela explique pourquoi il y a deux signes si l’on place deux expressions : il faut indiquer où est placé chacun des deux antécédents.
Ce n’est pas compliqué, mais il faut vraiment des exemples pour comprendre. Commençons par les expressions à un signe. On va supposer qu’on veut placer des x dans le tableau. On peut placer :
- une expression seule avec
- / xou+ / x; - une expression sur une double barre (prolongement par continuité) avec
-C / xou+C / x; - une expression suivie d’une zone interdite avec
-H / xou+H / x; - une expression suivie d’une double barre (discontinuité) avec
-D / xou+D / x; - une expression précédée d’une double barre (discontinuité) avec
D- / xouD+ / x; - une expression sur une double barre (prolongement par continuité) suivie d’une zone interdite avec
-CH / xou+DH / x; - une expression suivie d’une double barre (discontinuité) et d’une zone interdite avec
-DH / xou+DH / x.
Pour juste passer à l’expression suivante (ne rien faire), il faut utiliser R \.
Nous remarquons que les lettres sont quand même assez parlantes, et qu’elles sont combinées pour obtenir des choses plus complexes. On peut s’amuser à faire quelques petits tableaux avec tout ça.
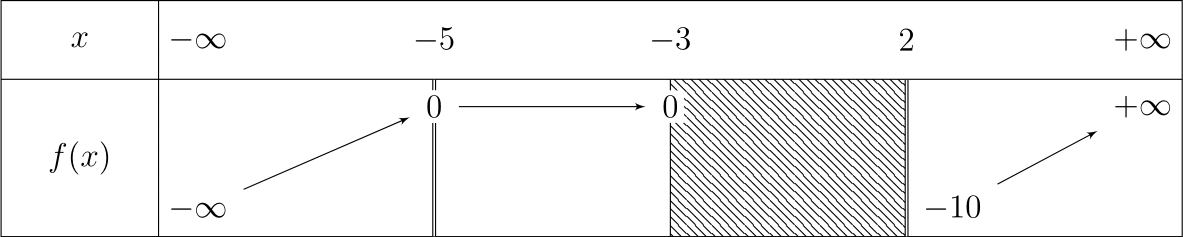
Voici un exemple qui utilise à peu près tout ce que nous avons vu.
\begin{tikzpicture}
\tkzTabInit{$x$ / 1 , $f(x)$ / 2}{$-\infty$, $-5$, $-3$, $2$, $+\infty$}
\tkzTabVar{-/ $-\infty$, +C/ $0$, +H/ $0$, D-/ $-10$, +/ $+\infty$}
\end{tikzpicture}
Il nous permet d’obtenir ceci.
Maintenant que nous avons vu les expressions à un signe, il est beaucoup plus simple d’aborder celles à deux signes. Il faudra juste faire attention au fait que le premier signe correspond au positionnement vertical de l’expression mathématique de gauche, et le deuxième signe à celui de l’expression mathématique de droite. Avec elles, on peut placer :
- deux expressions de part et d’autre d’une double barre (discontinuité) avec
+D-,-D+,+D+ou-D-; - une expression sur une double barre (continuité) et une expression après la double barre (discontinuité) avec
+CD-,-CD+,+CD+ou-CD-; - une expression avant une double barre (discontinuité) et une expression sur la double barre (continuité) avec
+DC-,-DC+,+DC+ou-DC-; - deux expressions avec
+V-,-V+,+V+ou-V-.
De même, les lettres sont assez parlantes. Nous avons maintenant tout pour faire de beaux tableaux de variations. Voici un exemple.
\begin{tikzpicture}
\tkzTabInit{$x$ / 1 , $f(x)$ / 2}{$-\infty$, $-5$, $-3$, 0, $+\infty$}
\tkzTabVar{-/ $-\infty$, +CD-/ $0$/ $2$, +D+/ $0$ /$0$, -V-/ $-2$ / $3$, +/ $+\infty$}
\end{tikzpicture}
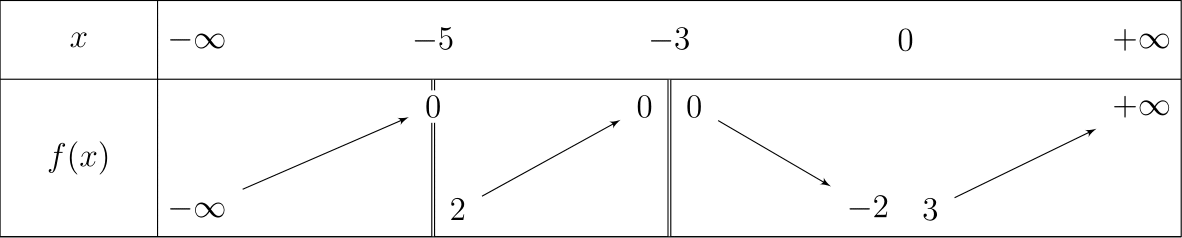
Nous voyons que V ne fait que placer les deux valeurs (oui ça peut paraître inutile).
tkzTab = \tkzTabInit , \tkzTabLine et \tkzTabVar
Maintenant, nous pouvons faire des tableaux de variations complets. Par exemple, si nous voulons tracer le tableau de variations de la fonction sinus sur l’intervalle , avec d’abord le tableau de signes de sa dérivée (donc de la fonction cosinus), il nous suffit d’utiliser \tkzTabInit pour initialiser un tableau, puis \tkzTabLine pour créer la ligne de signes de la fonction cosinus, et enfin celle de variations avec \tkzTabVar. On obtient finalement un code de ce type.
\begin{tikzpicture}
\tkzTabInit{$x$ / 1 , $\cos(x)$ / 1, $\sin(x)$ / 1.5}{$0$, $\dfrac{\pi}{2}$, $\pi$}
\tkzTabLine{, +, z, -, }
\tkzTabVar{-/ 0, +/ 1, -/ 0}
\end{tikzpicture}
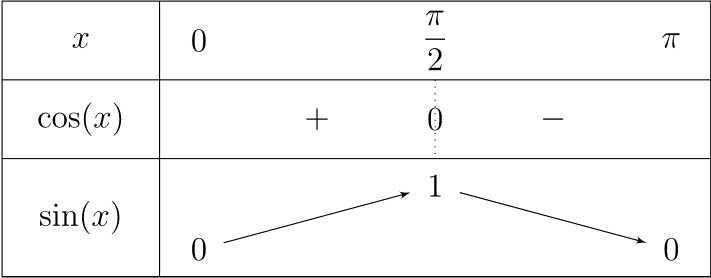
C’est cool, non ? Et il y a encore mieux. Si nous voulons faire un tableau du même type que celui que nous venons de faire —- à savoir un tableau de trois lignes, une pour les variables, une pour les signes et une pour les variations —- il existe une commande magique, la commande \tkzTab. Elle permet d’enchaîner les commandes \tkzTabInit, \tkzTabLine et \tkzTabVar. Elle prend comme argument les arguments que prennent ces trois fonctions (elle prend donc quatre listes en arguments). Ainsi, pour avoir le même tableau que précédemment…
\begin{tikzpicture}
\tkzTab{$x$ / 1 , $\cos(x)$ / 1, $\sin(x)$ / 1.5}{$0$, $\dfrac{\pi}{2}$, $\pi$}
{, +, z, -, }
{-/ 0, +/ 1, -/ 0}
\end{tikzpicture}
C’est un raccourci très utile. Mais n’oubliez pas, il ne s’utilise que dans ce cas particulier de tableaux.
Compléter nos tableaux
Nous pouvons maintenant faire des tableaux corrects. Il ne nous reste plus qu’à les compléter. Nous allons donc voir comment ajouter des valeurs sur une flèche d’un tableau de variations, comment ajouter des valeurs dans un tableau de signes…
Images intermédiaires sur une ligne de variations
Il existe deux commandes pour faire cela. Elles fonctionnent sensiblement de la même manière, mais ont quand même une différence : la première, \tkzTabVal, ne nécessite pas qu’un antécédent ait déjà été défini pour l’image que l’on veut placer, contrairement à la seconde \tkzTabIma.
À quoi cela peut-il servir ?
\tkzTabIma sert dans le cas où l’on a une valeur particulière pour un antécédent. Cependant, les variations de la fonction restent les mêmes, donc, on a utilisé R \ dans le tableau de variations. On peut alors l’utiliser pour rajouter la valeur. Par exemple, la fonction cosinus est décroissante sur , mais elle s’annule en . On peut alors utiliser \tkzTabIma pour faire apparaître ce 0 sur la flèche qui va de 1 () à -1 ().
\tkzTabVal permet également de placer une valeur sur une flèche. Cependant, elle ne demande pas qu’un antécédent ait déjà été défini. Ainsi, c’est à nous de donner la position de la valeur sur la flèche (plus ou moins proche de telle extrémité). Elle permet ainsi de placer une valeur sans antécédent, ce qui peut être utile si l’on veut faire ressortir une valeur de la fonction dont on ne connaît pas l’antécédent. De plus, elle peut aussi permettre d’associer à cette valeur un nouvel antécédent (celui-ci sera alors ajouté au tableau). On peut alors faire la même chose qu’avec \tkzTabIma.
Mais là où \tkzTabVal se révèle vraiment utile, c’est dans ce cas : on a une valeur particulière, on connaît son antécédent, mais on ne veut pas placer son antécédent, parce que l’on fait également le tableau de signes de sa dérivée, et cet antécédent n’est pas remarquable pour les signes de la dérivée.
Ces commandes doivent se placer juste après \tkzTabVar (ou \tkzTab). Ainsi, si nous avons un tableau avec plusieurs lignes de variations, la commande s’appliquera à la ligne de variations définie avec le \tkzTabVar précédent. De plus, nous pouvons utiliser plusieurs \tkzTabVal (ou \tkzTabIm) à la suite pour placer plusieurs valeurs sur les flèches. Par exemple…
\begin{tikzpicture}
\tkzTabInit[{$x$ /1, $f''(x)$ /1.5, $f'(x)$ /2, $f'(x)$ /1.5, $f(x)$ } {$0$ , $+\infty$}
\tkzTabLine{} % Signe de f''(x).
\tkzTabVar{} % Variations de f'(x).
\tkzTabVal{} % Ajout d’une valeur dans le tableau de variations de f'.
\tkzTabLine{} % Signe de f'(x).
\tkzTabVar{} % Variations de f(x).
\tkzTabVal{} % Ajout d’une valeur dans le tableau de variations de f.
\tkzTabVal{} % Ajout d’une autre valeur dans le tableau de variations de f.
\end{tikzpicture}
Nous savons maintenant comment elles doivent être placées. Voyons maintenant comment les utiliser.
Pendant toute cette partie, nous utiliserons l’exemple de la fonction cosinus sur .
\tkzTabVal
Voyons tout d’abord comment utiliser \tkzTabVal. Cette commande prend cinq paramètres obligatoires :
- le numéro de l’antécédent associé au début de la flèche (ce nombre est donc compris entre 1 et n - 1 avec n le nombre d’antécédents) ;
- le numéro de l’antécédent associé à la fin de la flèche (ce nombre est donc compris entre 2 et n avec n le nombre d’antécédents) ;
- la position de l’image sur la flèche (c’est un nombre décimal entre 0 et 1, qui correspond à la position de l’image par rapport au début de la flèche. Si c’est 0.1 l’image sera proche du début de la flèche, si c’est 0.5 elle sera à égale distance des extrémités de la flèche…) ;
- la valeur de l’antécédent (nous pouvons donner
{}pour ne pas associer d’antécédent) ; - la valeur de l’image (nous pouvons aussi transmettre
{}pour ne pas avoir d’image, mais, ce n’est pas très utile).
Voyons donc l’exemple avec la fonction cosinus.
\begin{tikzpicture}
\tkzTabInit{$x$ /1, $-\sin(x)$ /1, $\cos(x)$ /1.5} {$0$ , $\pi$}
\tkzTabLine{, -,}
\tkzTabVar{+/ 1, -/ -1}
\tkzTabVal{1}{2}{0.5}{}{$0$} % On place 0 mais il n’est associée à aucun antécédent.
\end{tikzpicture}
Et si on devait lui associer un antécédent…
\begin{tikzpicture}
\tkzTabInit{$x$ /1, $-\sin(x)$ /1, $\cos(x)$ /1.5} {$0$ , $\pi$}
\tkzTabLine{, -,}
\tkzTabVar{+/ 1, -/ -1}
\tkzTabVal{1}{2}{0.5}{$\dfrac{\pi}{2}$}{0} % On place 0, son antécédent est pi / 2.
\end{tikzpicture}
Voici le résultat obtenu.
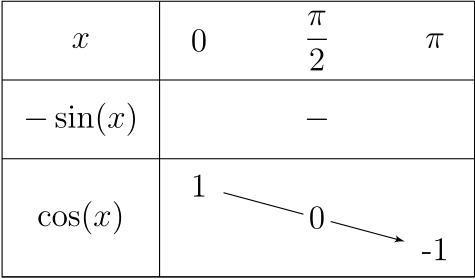
tkzTabVal.Il ne nous reste plus qu’à nous entraîner sur d’autres tableaux.
\tkzTabIma
Maintenant que nous avons vu la commande \tkzTabVal, la commande \tkztabIma est très simple à voir. Elle ne prend que quatre arguments obligatoires :
- le numéro de l’antécédent associé au début de la flèche (ce nombre est donc compris entre 1 et n - 1 avec n le nombre d’antécédents) ;
- le numéro de l’antécédent associé à la fin de la flèche (ce nombre est donc compris entre 2 et n avec n le nombre d’antécédents) ;
- le numéro de l’antécédent auquel correspond l’image (ce nombre est donc compris entre les deux nombres précédents) ;
- la valeur de l’image (là encore, nous pouvons donner
{}).
Voyons maintenant l’exemple de la fonction cosinus.
\begin{tikzpicture}
\tkzTabInit{$x$ /1, $-\sin(x)$ /1, $\cos(x)$ /1.5} {$0$ , $\dfrac{\pi}{2}$, $\pi$}
\tkzTabLine{, -, -1, -, }
\tkzTabVar{+/ 1, R/, -/ -1}
\tkzTabIma{1}{3}{2}{$0$}
\end{tikzpicture}
Le résultat…
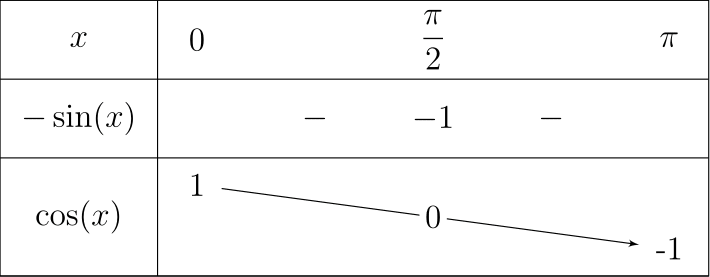
tkzTabIma.Nous somme obligés d’utiliser R/ pour bien construire notre tableau de variations, nous utilisons donc ensuite \tkztabIma pour rajouter l’image de .
Là encore, il faut nous entraîner. Ce n’est qu’après plusieurs utilisations que l’on peut être à l’aise avec ces deux commandes.
Images sur une ligne de signes
Nous allons maintenant voir comment placer des valeurs sur une ligne de signes en dehors des valeurs placées en définissant la ligne. Ceci nous permettra notamment de placer des limites à droite et à gauche…
Pour cela, nous allons utiliser la commande \tkzTabSlope. C’est l’une des commandes les plus simples que nous allons voir. Elle prend en paramètre une liste d’éléments séparés par une virgule (oui, ça nous rappelle des choses). Ces éléments sont de la forme i / eg / ed avec :
iest le rang de l’antécédent pour lequel on doit placer une valeur (donciest compris entre 1 et n) ;egcorrespond à la valeur que l’on souhaite placer à gauche (on peut ne rien passer en paramètre) ;edcorrespond à la valeur que l’on souhaite placer à droite (on peut ne rien passer en paramètre).
Nous pouvons déjà voir comment l’utiliser. Voici, un exemple avec le tableau de signes de la fonction logarithme.
\begin{tikzpicture}
\tkzTabInit{$x$ /1, $\ln(x)$ /1} {$0$ , $1$, $+\infty$}
\tkzTabLine{d, -, 0, +, }
\tkzTabSlope{1//-\infty, 3/+\infty/}
\end{tikzpicture}
On place un signe sous le premier antécédent à droite, et on place un signe sous le troisième antécédent à gauche.
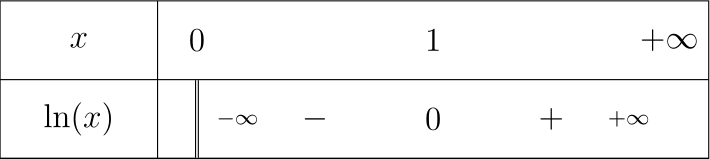
tkzTabSlop.L’utilisation de \tkzTabSlope n’est pas plus compliquée que cela.
Personnalisation
Nous avons maintenant tout pour faire des tableaux complets. Tkz-Tab propose évidemment d’autres choses, mais nous avons déjà vu quasiment tout ce qu’il était possible de faire.
Nous allons maintenant passer à la personnalisation de nos tableaux. Il peut en effet être bien de pouvoir rajouter sa touche sur son tableau, ou juste de changer quelques paramètres.
Voyons comment personnaliser la totalité du tableau. Cela se fait grâce aux options de la commande \tkzTabInit. Nous n’allons pas toutes les voir, mais seulement les principales.
Espacement
L’option escpl permet de modifier l’espacement entre deux valeurs. Il faut lui donner une valeur, l’unité étant le centimètre (par défaut, l’espacement entre deux valeurs est de 2 cm).
L’option lgt permet de modifier la largeur de la première colonne du tableau. Là encore, la valeur par défaut est de 2 cm et l’unité est le centimètre.
Ces deux commandes sont les principales options de \tkzTabInit.
L’option deltacl peut aussi servir dans le cas où nous voudrions définir l’espacement entre les valeurs et les extrémités du tableau. Au risque de me répéter, la valeur est encore une fois à donner en centimètres (la valeur par défaut est cette fois 0,5 cm).
Faisons un tableau en changeant ces paramètres.
\begin{tikzpicture}
\tkzTabInit[lgt = 2.5, espcl = 3, deltacl = 0.7]{$x$ / 1 , $f(x)$ / 1}{$0$, $6$, $8$, $+\infty$}
\tkzTabLine{z, -, d, h, d, +, }
\end{tikzpicture}
Pour ce résultat…

Couleur du tableau
Tkz-Tab permet aussi de colorer nos tableaux. Pour cela, il distingue quatre zones dans un tableau :
- la zone des antécédents (en haut à droite) ;
- la zone de la variable (en haut à gauche) ;
- la zone des fonctions (en bas à gauche) ;
- la zone des images (tout le reste du tableau en bas à droite, c’est-à-dire les variations, les signes…).
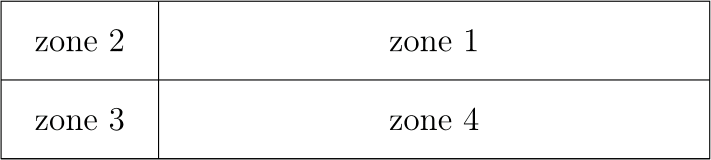
On peut donc attribuer à chacune de ces zones une couleur. Mais avant cela, il faut activer l’utilisation des couleurs. Pour cela, il faut donner à l’option color de \tkzTabInit la valeur true (ou plus simplement utiliser cette option). Il s’agit d’un booléen qui indique si l’on veut utiliser les couleurs.
Ensuite il ne reste plus qu’à donner à chaque zone une couleur. Pour cela, on dispose de quatre options :
colorL(comme « couleur de la ligne ») pour la zone 1 ;colorV(comme « couleur de la variable ») pour la zone 2 ;colorC(comme « couleur de la colonne ») pour la zone 3 ;colorT(comme « couleur du tableau ») pour la zone 4.
Grâce à ces options, mettons un peu de couleur dans un tableau.
\begin{tikzpicture}
\tkzTabInit[color, colorC = blue!15, colorL = green!15]
{$x$ / 1 , $f(x)$ / 1}{$0$, $6$, $8$, $+\infty$}
\tkzTabLine{z, -, d, h, d, +, }
\end{tikzpicture}
Et le résultat…

Nous pouvons changer l’épaisseur des traits du tableau avec l’option lw (par exemple, lw = 0.8pt) avec une épaisseur par défaut de 0,4 pt. Cependant, il est déconseillé de changer cette épaisseur, pour garder un document harmonieux.
Nous avons vu l’essentiel des personnalisations disponibles, même s’il en reste d’autres.
Nous avons maintenant tout pour faire nos beaux tableaux de variations. Pour apprendre à les personnaliser encore plus, nous pouvons consulter la documentation du package (en français, s’il-vous-plaît).
Merci à tous les membres et en particulier à Davidbrcz qui a validé ce tutoriel et à Dominus Carnufex pour ses corrections orthotypographiques.
Le logo de ce tutoriel est tiré de la documentation de Tkz-Tab. L’image est utilisée avec l’accord de son auteur.








