Graphes et représentation de graphe

• Bases de la théorie des graphes
• Sommaire
• Parcourir un graphe

Dans ce chapitre vous verrons la définition d'un graphe, ainsi que ses différentes caractéristiques remarquables.
Nous donnerons un premier aperçu des problèmes pouvant être identifiés comme des problèmes de graphe. Puis nous étudierons les deux principaux moyens de le stocker en mémoire.

• Dessine moi un graphe !
• Un peu de vocabulaire
• Représentations et stockage en mémoire

Dessine moi un graphe !

Le graphe

Ces points sont nommés nœuds ou sommets. Ces liens sont nommés arêtes.

Notez bien que ces fameux points n'ont pas de position absolue dans le plan, ni de position relative les uns aux autres. De la même façon, les arêtes ne sont pas forcées d'être droites (bien que conventionnellement on les représente comme tel par soucis de lisibilité) : elles peuvent se croiser, être courbées ou faire des détours, etc… Ainsi un graphe n'est pas une figure, bien que l'on puisse représenter un graphe par une figure. Les graphes ne se cantonnent donc pas à des considérations d’ordre purement géométrique, bien au contraire !

En effet, un graphe sert avant tout à manipuler des concepts, et à établir un lien entre ces concepts. N'importe quel problème comportant des objets avec des relations entre ces objets peut être modélisé par un graphe.
Il apparaît donc que les graphes sont des outils très puissants et largement répandus qui se prêtent bien à la résolution de nombreux problèmes.

En voici quelques uns.

Une carte, un labyrinthe, un lieu… et la recherche de chemins

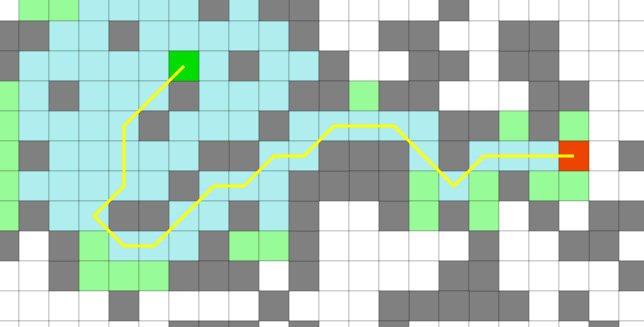
Il s'agit d'un cas très classique, notamment dans le domaine du jeu vidéo. Chaque nœud représente une position (ici une case libre) et chaque arête correspond à un chemin entre deux positions (ici deux cases libres adjacentes).
Il est courant de chercher le chemin le plus court entre deux positions : les IA s'en servent pour déplacer les créatures aussi vite que possible dans le monde virtuel. En remplaçant les nœuds par des adresses et les arêtes par des routes, on obtient le graphe utilisé par les GPS ou Google Map par exemple.
On utilise couramment le terme anglais pathfinding pour désigner la recherche de chemins dans un graphe.

Des relations entre individus

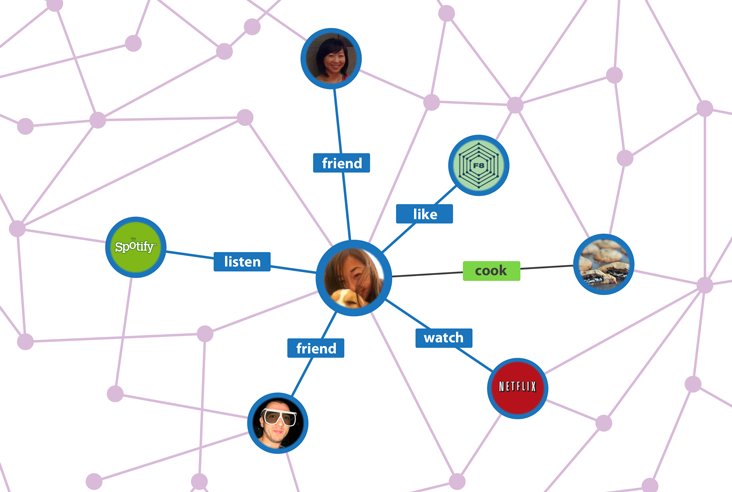
Cet outil est très utilisé en sciences sociales pour représenter des individus et leurs différents liens. On en fait usage dans le milieu de la recherche, mais aussi dans les réseaux sociaux. L'objectif va être de pouvoir identifier les communautés formées, les centres d'intérêt communs… Une exploitation intelligente de ces données est indispensable pour suggérer à l'utilisateur les choses qu'il est susceptible d'aimer, les personnes qu'il connaît peut-être, et avant tout (et surtout) pour créer des publicités ciblées adaptées à chacun.

Une anecdote à ce sujet : en moyenne seules 8 personnes vous séparent de n'importe quelle autre personne à la surface de la Terre. Si vous prenez la connaissance de la connaissance etc… d'une de vos connaissances, en moyenne 8 personnes permettront de vous connecter avec n'importe quel français, américain, indien ou japonais. Et il est rare de dépasser 11 ou 12. Il s'agit là du diamètre moyen du graphe social de l'humanité.

L’ordonnancement de tâches : le tri topologique

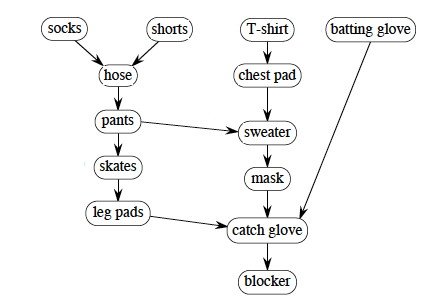
Les problèmes d'ordonnancement de tâches sont toujours un sujet de recherche active aujourd'hui. On peut représenter chacune des tâches à effectuer par un nœud, et les dépendances entre chacune des tâches par les arêtes. Ainsi, l’ordre dans lequel on enfile chaussettes et pantalon importe peu, mais il faut que les deux soient mis avant de lacer ses chaussures. De la même façon, on peut installer les câblages électrique et téléphonique dans l'ordre de notre choix, mais il faut que les murs soient construits avant !
On résout ce problème avec un tri topologique.

Minimiser l'usage de ressources avec les arbres couvrants minimaux

En parlant de câblage, vous souhaitez que toutes vos prises soient reliées au secteur, non ? Cela est simple ! Mais le fil électrique coûte cher au mètre et vous souhaitez minimiser le prix de votre installation.
Ainsi, vous associerez un nœud à chaque prise, et une arête à chaque fil qu'il est possible (mais pas nécessaire) d'installer. A vous de choisir l'ensemble de câbles les plus courts pour relier toutes les prises !
Cela correspond à la recherche de l'arbre couvrant minimal.

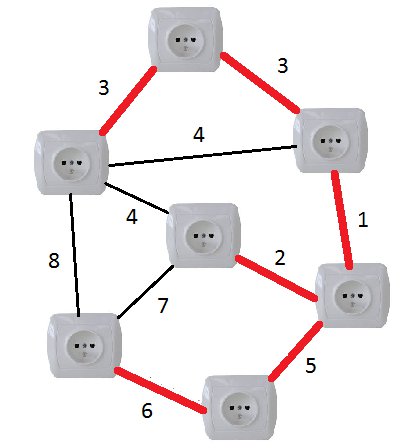
Ici l'ensemble de fils les plus courts est colorié en rouge.

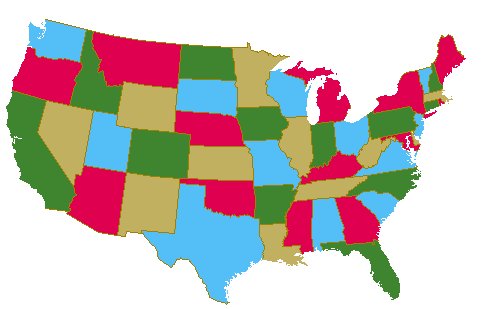
Tromper votre ennui en géographie en coloriant des cartes

Vous vous ennuyez à mourir en géographie. Comme vous êtes un individu froid et austère, mais aussi efficace, économe et démuni, vous souhaitez colorier cette triste carte en utilisant un minimum de couleurs, et en faisant en sorte que deux pays limitrophes ne soient jamais de la même couleur.
Il s'agit du problème de coloration de graphe. Pour une carte en 2D ne cherchez plus : la réponse est 4, mais ce n'est pas le cas de tout les graphes… en effet, dans un carte, chaque pays est un nœud, et les arêtes correspondent au frontières communes.

Poster du courrier

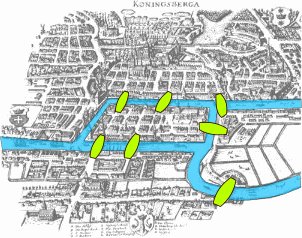
Vous êtes le facteur d'un petit village, vous distribuez le courrier à vélo, à la seule force de vos jambes. Vous devez passer devant toutes les maisons du village, ce qui implique de traverser toutes les rues. Mais soucieux de préserver vos forces et de renouveler continuellement votre découverte des paysages, vous ne voulez pas traverser deux fois la même rue. Ici chaque nœud est un carrefour, et chaque arête une rue. Vous êtes en train de chercher un circuit Eulérien !

Il doit son nom à Leonhard Euler, qui chercha à savoir s'il était possible de franchir les 7 ponts de Königsberg sans jamais repasser deux fois sur le même (et en ne traversant le fleuve que grâce aux ponts, bien entendu).

…et tout le reste !

Pensez à Youtube qui suggère des vidéos proches de celle que vous regardez (d'aucun prétendent qu'on finira toujours par aboutir à des vidéos de chats), pensez à wikipédia qui propose des articles connexes (nous reviendrons sur ce terme), pensez au cerveau humain, à ses milliards de neurones et à ses centaines de milliards de connexions entre eux ! Les graphes sont partout.

Apprenez à reconnaître un problème de graphe lorsque vous en voyez un, c'est déjà la moitié du travail. Il ne vous reste alors plus qu'à trouver l'algorithme qui répond à votre problème !

Un peu de vocabulaire

Quelques conventions et notations…

Maintenant que nous avons une idée de ce qu'est un graphe, tâchons d'employer un vocabulaire précis pour traiter de chacune de ses caractéristiques. Certains algorithmes ne fonctionnent que sur des graphes possédant certaines particularités.

Pouvoir décrire en quelques mots les caractéristiques principales d'un graphe est donc indispensable, et vous devez toujours avoir le réflexe de le faire sitôt le graphe identifié. Cela vous guidera vers le choix de l'algorithme approprié.

Fixons d'ores et déjà quelques notations, par soucis de clarté. Ces notations sont conventionnellement utilisées dans la plupart des cours ou articles parlant de graphes.

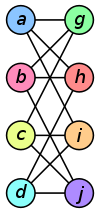
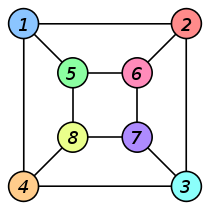
L'ensemble des nœuds du graphe est désigné par $N$. L'ensemble des arêtes est désigné par $A$. Le graphe $G$ est simplement défini comme $G = (N,A)$. Ainsi, la représentation du graphe importe peu : les deux graphes ci-dessous sont isomorphes (ici, on peut traduire grossièrement ce terme barbare par équivalents).

Graphe simple ou multigraphe

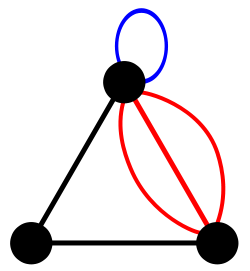
Une boucle est une arête qui relie un nœud à lui même.
Un lien double caractérise l'existence de plusieurs arêtes entre deux nœuds donnés.
Un graphe possédant l'une ou l'autre de ces caractéristiques est dit multigraphe. Un graphe ne possédant aucune des deux est dit graphe simple.
Nous travaillerons exclusivement sur des graphes simples par soucis de simplicité : ils couvrent la plupart des utilisations, et sont plus simples à traiter que les multigraphes dans le cas général.

Connexité

Un graphe est dit connexe lorsqu'il existe un chemin entre toute paire de nœuds. Une composante connexe d'un graphe est un sous-graphe connexe de ce graphe. Un sous-graphe est un sous-ensemble de nœuds du graphe, avec une partie de leurs arêtes associées. Ainsi, sur le dessin ci-dessous, vous ne voyez qu'un seul et unique graphe, comportant 3 composantes connexes.

Graphes orientés et non-orientés

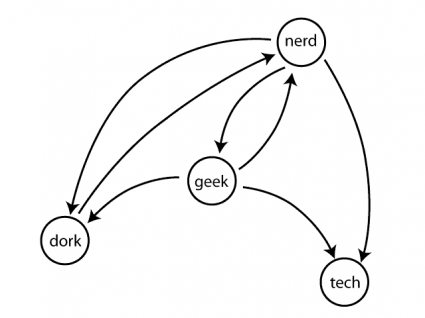
Voici une autre caractéristique fondamentale d'un graphe. Dans un graphe orienté les arêtes sont à sens unique. On les représente donc avec une flèche sur les dessins. D'ailleurs, le terme employé n'est plus arête, mais arc. Cette distinction est importante, car nombre d'algorithmes ne fonctionnent tout simplement pas sur des graphes orientés. Notez bien que cela n'empêche en rien que deux nœuds puissent être reliés dans les deux sens : il suffit d'utiliser deux arcs, chacun dans un sens (cela ne rompt pas la condition de graphe simple).

Graphes pondérés

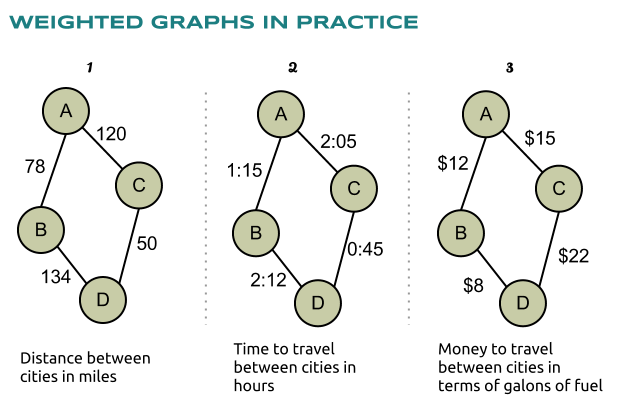
Dans un graphe pondéré les arêtes (ou les arcs) sont, ben, pondérés, quoi. Autrement dit, on associe une valeur à chaque arête. Elles peuvent très bien être négatives.
Cela peut-être une distance : lorsque que l'on cherche un plus court chemin entre deux nœuds, il va de soit que la somme des pondérations des arêtes doit être aussi petit que possible.
Mais ça peut aussi être un réel dans $[0;1]$ pour désigner des probabilités dans les chaînes de Markov par exemple. Cela peut aussi être un score, un prix, etc. N'importe quelle quantité qui peut vous passer par la tête !

Graphes cycliques

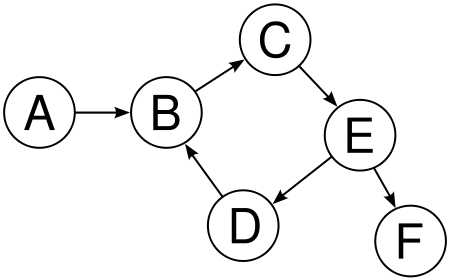
Un graphe cyclique comporte au moins un cycle. Un cycle est un chemin qui permet de relier un nœud à lui même, sans jamais passer deux fois par la même arête. Un graphe comportant cette propriété peut-être orienté ou non orienté (indifféremment).
La détection de cycles est d'ailleurs un problème récurrent en informatique, notamment lorsqu'on s'intéresse aux dépendances d'un fichier ou d'un programme : A requiert B, B requiert C, et C requiert A est un cas de dépendances cyclique habituel.

Les graphes ne possédant pas de cycles dont dit acycliques. Il existe un sous-ensemble remarquable de graphes acycliques : les DAG (pour Directed Acyclic Graph); ce sont des graphes acycliques orientés. Les algorithmes dynamiques (nous verrons ça plus tard) ne peuvent travailler que sur des DAG.

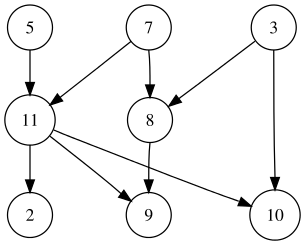
Densité d'un graphe et degré d'un nœud

La densité d'un graphe correspond au rapport du nombre d'arêtes sur le nombre total d'arêtes possibles. C'est donc un réel compris entre $0$ et $1$. Cette caractéristique influe sur le choix de sa représentation.
Une densité de $0$ correspond à un graphe sans arêtes où tout les sommets sont isolés.
Une densité de 1 correspond à un graphe complet : chaque nœud est relié à chaque autre nœud.

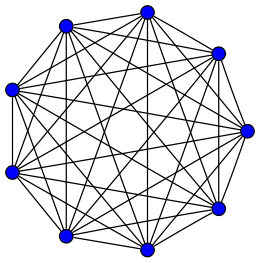
Dans un graphe simple orienté de $N$ nœuds, chaque nœud ne peut être relié qu'à ses $N-1$ voisins au maximum, soit un total de $N(N-1)=N^2-N$ arcs.
Et $\frac{N^2-N}{2}$ arêtes dans le cas d'un graphe non orienté.

Le degré d'un nœud correspond au nombre d'arêtes reliées à ce nœud. Dans le cas d'un graphe orienté, le degré entrant d'un nœud est le nombre d'arcs qui aboutissent à ce nœud, et le degré sortant le nombre d'arcs qui partent de ce nœud.

De façon générale, lorsque le nombre d'arêtes d'un graphe est de l'ordre de $N$, le graphe est dit creux. Le degré moyen de ses nœuds est une constante. A l'inverse, lorsque le nombre d'arêtes est de l'ordre de $N^2$, le graphe est dit dense : le degré moyen de ses nœuds est de l'ordre de $N$.

Arbre

Un graphe est un arbre s'il vérifie les propriétés suivantes : il est acyclique, non orienté, et connexe. De cela il découle qu'il n'existe qu'un et un seul chemin entre deux nœuds donnés (c'est vraiment très pratique, je vous l'assure !).

Attardons sur quelques évidences. Un arbre possède une seule et unique racine. Il relié à d'autres nœuds - ses fils - par des branches (le terme arête demeure correct toutefois). Tout les nœuds peuvent posséder 0, 1 ou plusieurs fils. En revanche, ils possèdent tous un seul et unique père, à l'exception de la racine qui n'en a pas. Les feuilles sont caractérisées par l'absence de fils.

Un dessin pour mieux comprendre tout ce fouillis :

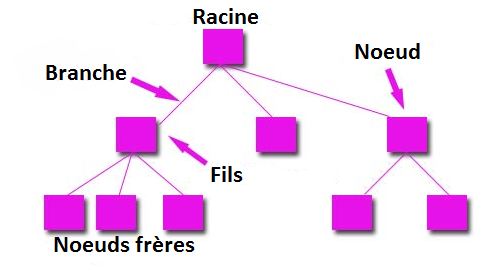
Comme vous pouvez le voir, les nœuds correspondent à des embranchements. Si on part d'un nœud et qu'on descend de fils en fils, on aboutira nécessairement à une feuille. Et si on remonte de père en pères, on aboutit à la racine (et dire qu'il y a encore des gens qui doutent du créationnisme !).

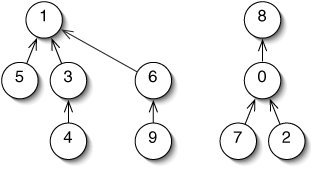
Si le graphe n'est pas connexe mais qu'il possède les propriétés cités ci-dessus, alors chacun des sous-graphes connexes est un arbre, et l'ensemble forme une forêt (ben oui, un ensemble d'arbres c'est une forêt).

Graphe biparti

Un graphe est biparti s'il est possibles de former deux partitions (comprendre, de le couper en deux morceaux distincts) de ses sommets de façon à ce que chaque arête passe d'une partition à l'autre, sans que jamais une arête ne relie deux nœuds dans la même partition.

Une fois encore, un joli dessin vaut tout les discours du monde.

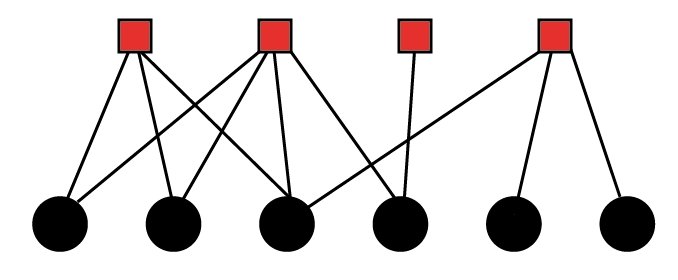
J'imagine que l'intérêt doit vous paraître limité pour le moment. Mais les graphes bipartis servent dans plein de situations, et à pleins de choses différentes, comme représenter une relation binaire par exemple.

Remarquez qu'un arbre est forcément un graphe biparti. En effet, les nœuds à profondeur paire sont "pris en sandwich" entre des nœuds à profondeur impaire (son père et ses fils), et vice-versa. Ainsi deux nœuds à une profondeur de même parité ne seront jamais reliés par une arête, on peut donc former une partition contenant les nœuds de même parité.

Représentations et stockage en mémoire

Généralités

Maintenant, cher lecteur, nous avons une idée bien plus précise de ce qu'est un graphe. Mais il n'est pas destiné à rester un outil purement théorique ! Il faut pouvoir résoudre des problèmes avec, et donc implémenter des algorithmes qui travaillent dessus.

Nous devons donc trouver une structure de données adaptée pour le stocker, qui soit économe en mémoire, et qui permette aux algorithmes de l'exploiter rapidement.

Chaque nœud est stocké dans un tableau, une liste, ou n'importe quelle autre structure de données plus complexe (aucune contrainte particulière à ce propos, à vous de choisir la plus adaptée). Il est composé de propriétés, comme par exemple une position, une lettre, une valeur ou n'importe quelle entité plus complexe, qui dépend du problème (au cas par cas).

La difficulté consiste donc à lister intelligemment les arêtes entre les nœuds.
On résout ce problème avec une liste d'adjacence ou une matrice d’adjacence. La quasi totalité des implémentations d'un graphe sont des variantes de ces deux structures de données.

Attention ! La liste et la matrice ne sont pas seulement des structures de données, elles sont aussi une représentation du graphe.
La matrice et la liste contiennent suffisamment d'informations pour définir le graphe, au même titre que la représentation géométrique à base de sommets et d'arêtes.
Mais contrairement à cette dernière, qui est plus intuitive et plus adaptés aux êtres humains, la matrice et la liste peuvent être aisément implémentées sous forme de structure de données et utilisées par un programme.

La liste d'adjacence

La liste d’adjacence est le moyen le plus répandu pour stocker un graphe en mémoire : elle correspond à la représentation intuitive que l'on s'en fait. La liste d'adjacence d'un nœud est la liste de ses voisins (ou la liste des arêtes qui le relie à ses voisins).

1
2
3
4
5
6
7

struct Noeud
{
     proprietes
     voisins []
}  

Noeud noeuds [] = graph

Fin de la théorie.

Passons à la pratique : vous pouvez avoir, selon ce que vous propose votre langage, plusieurs moyens de stocker la liste des voisins.

1) Des indices et un tableau

C'est la façon la plus naturelle, et la plus triviale. Vous mettez tout vos nœuds dans un tableau, et la liste d'adjacence de chaque nœud contient l'indice de ses voisins. En raison de sa simplicité et de son expressivité, c'est l'implémentation qui sera utilisée dans la suite du tutoriel.

Voici un moyen d'itérer sur tout les voisins du nœud indexé par courant.

1
2

Pour chaque voisin V dans noeuds[courant].voisins
     faire quelque chose avec noeuds[V]

Le facteur constant d'accès à chaque voisin est très faible, ce qui vous permet de vous "promener" très rapidement dans le graphe. Vous pouvez généralement obtenir de très bonnes performances de cette façon.

Le seul inconvénient de cette méthode est de devoir disposer de l'intégralité du graphe dans la mémoire. Problématique si vos ressources en mémoire sont limitées, ou si pire, le graphe est de taille infinie !
Cela impose également que vous connaissiez dès le début l'ensemble du graphe, ce qui n'est pas toujours le cas : il en résulte une représentation figée qui interdit toute modification de certaines données (nombre de nœuds… ), et se limite à leur simple exploitation (ce qui demeure suffisant pour la plupart des algorithmes, en particulier tout ceux que nous étudierons).

2) Des hash et une table de hashage

Il s'agit de la version adaptée de l'implémentation précédente, pour palier à son principal défaut. Tout les nœuds que vous connaissez déjà sont stockés dans une table de hachage, et la liste d'adjacence de chaque nœud contient le hash de ses voisins. C'est généralement l'implémentation idéale pour un graphe dans lequel les arêtes entre chaque nœud sont définies par des règles précises, et non pas de manière purement arbitraire.

Prenons l'exemple du jeu d'échecs : en associant à un nœud à chaque position, on constate que les arêtes correspondent à chaque coup légal qui mène à une position légale elle aussi (le milieu des jeux de stratégie semble très policé). Ainsi, pour chaque nœud, on peut facilement lister ses voisins.

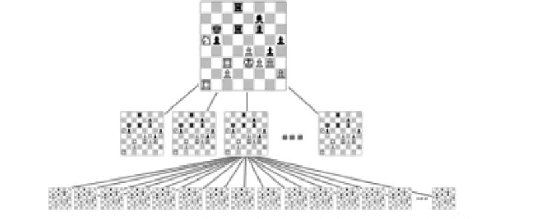
Il n'est pas possible de stocker autant de nœuds que de configurations du plateau : il en existe de l'ordre de $10^{50}$ !
Mais ce n'est pas un problème : jouer une partie revient à se promener dans ce graphe (c'est d'ailleurs un arbre), et il n'est en rien nécessaire d'énumérer tout les nœuds pour cela.

Le principal défaut de cette implémentation est le calcul des hashs : cela se fait en $O(1)$ en temps mais avec un facteur constant très important.

3) Des pointeurs

Cette implémentation est à réserver aux langages qui supportent ce concept (langages bas-niveaux essentiellement).

La liste d'adjacence contient des pointeurs vers chaque nœud voisin. Chaque nœud est alloué dynamiquement. Cela permet une représentation très souple du graphe : ajout et suppression de nœuds, et d'arêtes. Pour reprendre un précédent exemple : sur des réseaux sociaux des comptes peuvent être supprimés ou ajoutés, et on peut "aimer" ou "ne plus aimer" certaines choses, etc…

Cependant, la construction du graphe et son exploitation n'est pas facile : cette implémentation sujette aux bugs est à réserver aux cas dans lesquels elle est absolument nécessaire.

Conclusion

Voici quelques caractéristiques remarquables de la liste d'adjacence :

• Complexité en mémoire : $O(N+A)$
• Complexité en temps pour itérer sur tout les voisins d'un nœud : $O(d)$ avec $d$ le degré sortant du nœud
• Ajout d'arête : $O(1)$
• Retrait d'arête : $O(d)$ car il faut la retrouver avant de la supprimer
• Tester si deux nœuds sont voisins : $O(d)$ car il faut itérer naïvement sur toutes les arêtes de l'un des deux nœuds

Variante :

Plutôt que d'utiliser une liste, vous pouvez utiliser un arbre binaire de recherche équilibré :

• Ajouts et retraits d'arêtes en $O(\log{d})$
• Tester si deux nœuds sont voisins en $O(\log{d})$
  En effet les opérations pour retrouver les arêtes sont plus rapides, mais en contre-partie leur ajout est plus long. Cette optimisation n'est raisonnablement valable que lorsque le degré des nœuds devient important (en particulier, en dessous de 8 les gains sont souvent invisibles, mais des tests s'imposent en toutes circonstances, ne faites pas de cette indication une généralité !).

N'oubliez pas que la construction du graphe au préalable nécessite un ajout des arêtes une à une, soit ici une construction du graphe en $O(N)$ contre $O(N\log{N})$.

Choisissez l'implémentation la plus adaptée à votre problème, faites un compromis, ou inventez en d'autres…

La matrice d'adjacence

La matrice d'adjacence est un tableau en deux dimensions. Chacune des dimensions est indexée par les nœuds du graphe (typiquement de $0$ à $N-1$).
A l'intersection de chaque ligne et colonne on trouve un nombre : il vaut 1 si une arête relie les deux nœuds indexés par les coordonnées de la case, et 0 sinon.

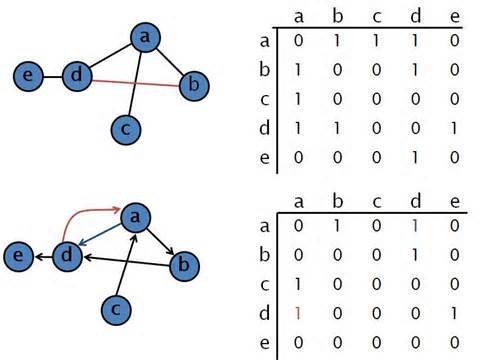
On observe plusieurs choses intéressantes.

• Les boucles reliant un nœud à lui même sont sur la diagonale de la matrice.
• Cette matrice est symétrique par rapport à sa diagonale dans un graphe non-orienté (puisque si A est relié à B, alors B est relié à A).
• Si le graphe ne comporte aucune arête, alors c'est la matrice nulle.

• Si le graphe est creux, alors la matrice le sera aussi.

• Pour $N$ nœuds, cette matrice est de taille $N\times N$. Soit une complexité de $O(N^2)$ en mémoire. Si votre langage le permet, vous pouvez stocker chacun des booléens sur un bit; il en résulte une consommation en mémoire de $\frac{N^2}{8}$ octets exactement, ce qui est très compact (incompressible dans le cas général).

• Vous pouvez itérer sur tout les voisins d'un nœud en $O(N)$
• En outre, à tout moment vous pouvez déterminer si deux nœuds sont voisins (c'est à dire reliés par une arête) en $O(1)$
• Pour finir les ajouts et retraits d'arêtes se font en $O(1)$

Si cette représentation est couteuse pour un graphe creux (on lui préférera la liste d'adjacence), elle devient très rentable pour un graphe dense.
La densité est souvent le critère décisif du choix entre la matrice ou la liste.

Si le graphe est pondéré, vous pouvez remplacer les booléens par des nombres correspondant à la pondération de chaque arête. Et vous fixez une valeur spéciale pour signifier l'absence d'arête ($-1$, $0$ ou $\infty$ par exemple, selon les cas).

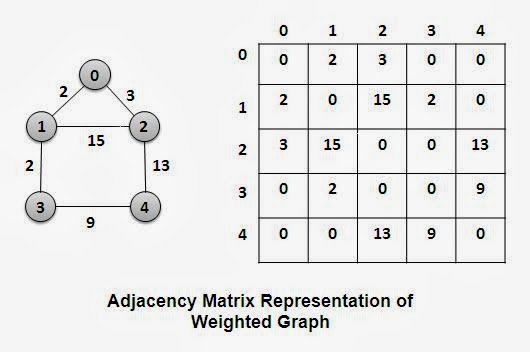
Les matrices d'adjacence sont particulièrement usitées lors de démonstrations sur un graphe, car la matrice est un outil mathématique bien connu.

Conclusion

Un petit tableau récapitulatif fera l'affaire.

Autres représentations

Il existe bien d'autres représentations d'un graphe.

Citons particulièrement la matrice d’incidence.
C'est une matrice de dimensions $N\times A$ qui indique quels liens arrivent sur quels sommets.
A l'intersection d'une ligne correspondant à nœud et d'une colonne correspondant à une arête on trouve un nombre.
Il vaut $0$ si cette arête n'est pas reliée à ce nœud.
En revanche, si ce nœud est une extrémité de l'arête, ce coefficient diffère selon si le graphe considéré est orienté ou non.
Pour un graphe non orienté, cette valeur vaudra alors $1$ dans le cas général, et $2$ si cette arête réalise une boucle sur ce nœud (car ce nœud est deux fois l'extrémité de cette arête). Ainsi la somme des coefficients sur une colonne vaudra toujours 2.
Pour un graphe orienté ce coefficient vaut $-1$ si l'arc sort du nœud considéré, et $1$ lorsque l'arc entre dans le nœud.

La raison pour laquelle je ne vous l'ai pas proposée en structure de données est simple : ses performances sont en tout point inférieures à celles de la liste ou de la matrice d'adjacence, quelque soit l'opération considérée. La consommation en mémoire, du $O(N\times A)$, soit un $O(N^3)$ en pire des cas, est aberrante si le graphe est dense.

Alors, pourquoi cette représentation a été inventé, me direz-vous ?
Eh bien il se trouve que les graphes sont des objets mathématiques comme les autres, et leurs différentes représentations ont nécessairement des liens entres elles. Des relations relient la matrice d'incidence avec la matrice Laplacienne, la matrice d'adjacence, la matrice des degrés ou encore le line graph.
Cela sert dans des calculs, et occasionnellement dans certains algorithmes.

Il y a cependant trop de choses à dire sur chacun de ces sujets pour que je m'y risque ici. Les curieux pourront approfondir leurs recherches.

• Bases de la théorie des graphes
• Sommaire
• Parcourir un graphe