Les arbres binaires de recherche

Lorsque l'on parle d'arbres, bien des gens penseront de prime abord à la biologie, la botanique et donc aux arbres tels que vous pouvez sûrement les voir en jetant un coup d'œil par votre fenêtre. Cependant, les arbres se retrouvent dans un ensemble de domaines tous plus variés les uns que les autres, et c'est sur l'algorithmique que nous allons nous pencher ici. Les arbres ont effectivement inspiré les algorithmiciens de la deuxième moitié du vingtième siècle, les amenant à créer une structure de données révolutionnaire : les arbres binaires de recherche.

Qu'est-ce que c'est, à quoi ça sert, comment ça marche, comment les implémenter, comment les améliorer ; ce sont autant de questions qui seront abordées dans ce cours, qui va, je l'espère de tout cœur, vous brancher sans vous faire prendre racine !

• Définitions
• Opération et implémentation
• Inconvénients et évolutions

Définitions

Structure de données

Comme mentionné dans l'introduction, les BST font partie de la grande famille des structures de données. Mais qu'est-ce donc que ces bêtes là ? Pour répondre à cette question, Wikipédia nous fournit un bon point de départ :

Il existe de très nombreuses structures de données différentes : enregistrements, listes, matrices, piles, files, tables ou encore… arbres. Toutes ont leur propre logique, leur propre manière de fonctionner et leurs propres avantages et inconvénients. Je vous laisse vous documenter sur ces nombreux sujets si le cœur vous en dit.

Les arbres binaires de recherche

Nous allons tâcher maintenant de définir précisément ces fameux arbres binaires. Pour se donner une idée, voici un exemple :

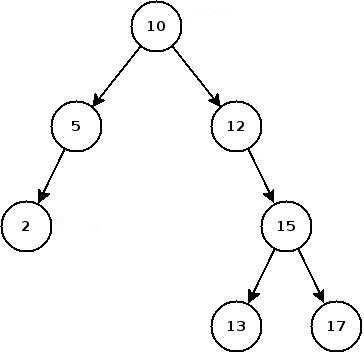
Arbre

On retrouve dans la vie de tous les jours de nombreuses arborescences : les dossiers d'un ordinateur, l'organisation d'une entreprise, et cætera. De manière un peu plus formelle, un arbre est un ensemble d'éléments appelés nœuds, parmi lesquels on trouve une unique racine : c'est le nombre 10 dans l'exemple. Chaque nœud est relié à ses descendants grâce à des arêtes. Les nœuds sans aucun descendants sont appelés feuilles ; dans l'exemple, il y a trois feuilles : 2, 13 et 17. Pour poursuivre avec le vocabulaire lié aux arbres, on appelle profondeur d'un nœud « l'étage » du nœud en question¹. Par exemple, le nœud contenant 5 a une profondeur égale à deux. Enfin, la hauteur désigne la profondeur la plus grande atteinte dans l'arbre. Ici, la hauteur de l'arbre est quatre : il s'agit de la profondeur des nœuds 13 et 17.

Binaire

La particularité d'un arbre binaire est que chaque nœud a au maximum deux fils : un à gauche et un à droite. Cette propriété a de nombreuses conséquences :

• On peut déceler dans les arbres binaires une structure récursive ; en effet, un arbre binaire est essentiellement composé d'un nœud, d'un sous-arbre gauche et d'un sous-arbre droit, chaque sous-arbre étant à son tour un arbre composé d'un nœud et de deux sous-arbres et ainsi de suite, jusqu'aux feuilles dont les sous-arbres sont vides.

• Chaque nœud ne possédant au maximum que deux descendants, un arbre de hauteur $h$ peut contenir au maximum $2^h-1$ nœuds. Inversement, un arbre contenant $n$ nœuds a une hauteur minimale de $\left\lceil\log_2(n)\right\rceil$.

De recherche

Les éléments stockés dans un arbre binaire de recherche doivent posséder une relation d'ordre totale, c'est-à-dire qu'il doit exister une manière de dire si un élément est plus grand ou plus petit qu'un autre. Par exemple, on peut trier des nombres par valeur ou des personnes par ordre alphabétique de leur nom de famille.

Le premier élément inséré dans l'arbre devient la racine. Ensuite, il suffit de mettre à gauche les éléments plus petits et à droite les éléments plus grands. C'est cette particularité qui rend les BST intéressants : la plupart des opérations réalisées sur les arbres binaires de recherche ont une complexité temporelle logarithmique ($O(\log\,n)$) dans le cas moyen. Cela est dû au fait que, grâce à la relation d'ordre liant les valeurs, on peut naviguer dans l'arbre avec une logique rappelant une recherche dichotomique, ce qui est plus performant que les listes, par exemple, que l'on doit parcourir élément par élément².

Exemple

Afin de tirer les choses au clair, voici un exemple d'utilisation des arbres binaires de recherche, afin que vous puissiez les voir en action. Un vétérinaire voudrait stocker les fiches médicales de ses patients, et, plutôt que d'utiliser un tableau ou une liste, on se propose d'utiliser un arbre binaire. La fiche contiendra différentes informations sur l'animal ; on utilisera son nom comme clé (c'est-à-dire comme critère pour la relation d'ordre), que l'on triera selon l'ordre alphabétique croissant.

Le vétérinaire reçoit sa première patiente, qui répond au nom de Gaufrette. Comme sa fiche sera le premier nœud de notre arbre, elle en devient automatiquement la racine.

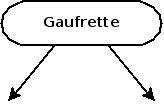
Après Gaufrette, vient le tour de Charlie. Une fois sa fiche remplie, on va l'ajouter à l'arbre : comme Charlie est avant Gaufrette dans l'ordre alphabétique, on place la fiche de Charlie à gauche de la racine.

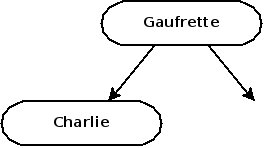
Le prochain patient est Médor. Vous l'aurez compris, Médor vient après Gaufrette, on placera donc sa fiche à droite de la racine.

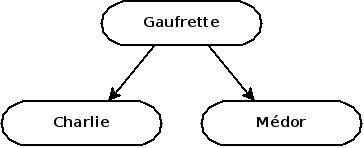
Allez, c'est à vous de jouer à présent ! Les trois prochains patients s'appellent Flipper, Bubulle et Augustin, et ils sont soignés par le vétérinaire dans cet ordre. Prenez quelques instants pour deviner à quoi ressemble l'arbre après ces nouvelles consultations. La solution se trouve juste après.

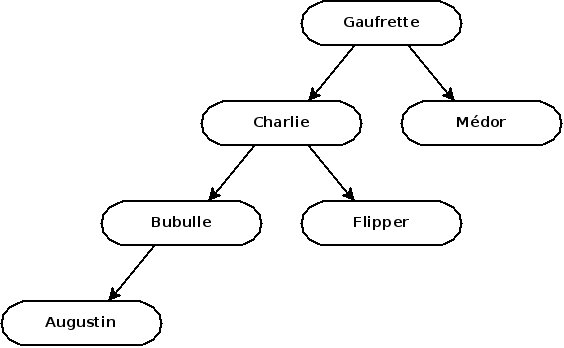
La structure d'un arbre est dépendante de l'ordre dans lequel on insère les éléments ! Si on avait ajouté Augustin avant Bubulle, l'arbre aurait été comme ceci :

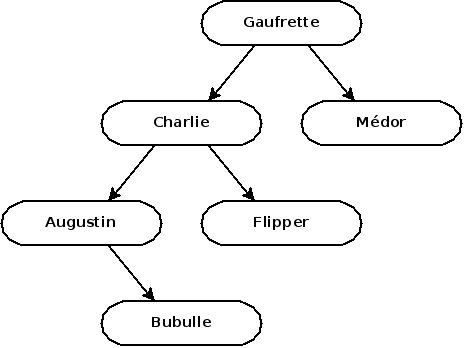
Nous reviendrons bien plus tard sur les implications de cette propriété, mais sachez que c'est très loin d'être anodin.

Opération et implémentation

Le but ici est de détailler l'implémentation des opérations sur les arbres binaires. Les algorithmes seront détaillés en pseudo-code par souci de généralisme, et une implémentation en C sera proposée afin d'approcher les algorithmes d'un point de vue un peu plus technique. Bien sûr, rien ne vous empêche de suivre le cours si vous ne connaissez pas le C, voire même de publier votre propre bibliothèque dans le langage de votre choix ! Comme toujours sur Zeste de Savoir, toute contribution est la bienvenue !

Définition de la structure

Ne mettons pas la charrue avant les bœufs : avant de penser aux fonctions destinées à être utilisées sur des BST, il faut peut-être commencer par définir les BST eux-mêmes, non ?

Pseudo-code

Du point de vue algorithmique, un BST n'a rien de très compliqué. Un nœud contient une donnée quelconque, un nœud fils à gauche, et un nœud fils à droite. On retrouve la structure récursive évoquée précédemment.

1
2
3
4

Structure bst_node :
    data est de type quelconque
    left est de type bst_node
    right est de type bst_node

On peut remarquer que les champs left et right peuvent être vides : dans le cas d'une feuille, par exemple, le nœud contient une donnée, mais n'a ni fils gauche, ni fils droit.

Enfin, pour définir l'arbre, on n'a besoin de connaître une seule chose : sa racine. En effet, une fois que la racine est connue, on peut accéder à ses successeurs, puis aux successeurs de ses successeurs, et ainsi de suite…

C

En C, en revanche, c'est un peu plus compliqué. Voici la structure qui sera utilisée pour les implémentations à suivre :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

typedef int (*orderFun)(void *, void *);
typedef void (*freeFun)(void *);

typedef struct _bst_node {
  void* data;     /**< The node's data */
  struct _bst_node* left;     /**< The node's left sub-tree */
  struct _bst_node* right;    /**< The node's right sub-tree */
} bst_node;

typedef struct {
  size_t data_size; /**< Size of an element */
  bst_node* root; /**< Root of the bst */
  orderFun compare; /**< Binary relation of the tree dataset */
  freeFun free; /**< Dynamic deallocation of tree data */
} bst;

Pour que la bibliothèque soit générique (c'est-à-dire qu'elle fonctionne quelque soit le type des données stockées dans l'arbre), le C nous propose le type void*. Cependant, on a besoin de connaître la taille d'une donnée (appelée data_size dans la structure C), ainsi que la fonction à utiliser pour réaliser la relation d'ordre, désignée par compare dans la structure.

1

typedef int (*orderFun)(void *, void *);

Enfin, on retrouve la fonction free de signature void free(void *). Cette fonction sera utilisée lors de la désallocation d'un nœud (lors d'une suppression ou de la destruction de l'arbre, par exemple) de sorte à éviter toute fuite de mémoire, dans le cas où les nœuds de l'arbre contiendrait des données allouées dynamiquement.

Comme vous le voyez, tout cela se révèle être beaucoup plus complexe que la structure algorithmique de l'arbre. Néanmoins, on peut écrire une fonction afin de rendre sûr et transparent la création d'un arbre, regardez :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

/**
 * \brief     Creates a tree
 *
 * Use this function to create a new tree. Make sure you respect
 * the following conditions since some @c asserts are used to check the
 * parameters relevance.
 * 
 * To deallocate the tree, use @ref bst_destroy
 *
 * \param     data_size   The size of an element; must be > 0.
 * \param     orderFun    The tree's binary relation; cannot be @c NULL.
 * \param     freeFun     The tree's data freeing function; can be NULL.
 *
 * \return    A pointer to the allocated tree
 *
 * \warning   Breaking any of the above conditions will cause the program to
 * abort!
 * \warning   Not deallocating the tree with @ref bst_destroy will result in
 * memory leaks!
 *
 * \see   bst_destroy
 */
bst* bst_new(size_t data_size, orderFun compare, freeFun free) {
  assert(data_size > 0);
  assert(compare);

  bst* tree = malloc(sizeof(bst));
  if(!tree) {// If allocation failed
      perror("malloc");
      exit(EXIT_FAILURE);
  }
  tree->data_size = data_size;
  tree->compare = compare;
  tree->free = free;
  tree->root = NULL;

  return tree;
}

Ajout d'un nœud

Pseudo-code

Comme nous l'avons vu précédemment on peut ajouter un nouveau nœud à l'arbre très simplement à l'aide d'une fonction récursive :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

Procédure bst_add (node de type bst_node, element de type quelconque) :
    Si node est vide
        node.data := element
    Sinon
        Si node.data > element
            bst_add(node.left, element)
        Sinon
            bst_add(node.right, element)
        FinSi
    FinSi

Comme le nœud node.left (respectivement node.right) de la racine peut être considéré comme la racine du sous-arbre gauche (droit), on peut utiliser la fonction elle-même pour réaliser l'insertion dans le sous-arbre, et répéter l'opération jusqu'à atteindre un sous-arbre vide, où l'on vient insérer la nouvelle donnée.

C

Ici, nous allons utiliser exactement la même méthode. Néanmoins, les structures pseudo-code et C étant différentes, les fonctions le seront un peu aussi. Regardons pour commencer la signature de la fonction bst_add en C :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

/**
 * \brief   Adds a new node to a tree
 *
 * Calling this function dynamically allocates a new node and inserts it into
 * the binary search tree.
 *
 * \param   tree    The tree to insert the new node into. Cannot be @c NULL
 * \param   element     The new node's data. Cannot be @c NULL
 */
void bst_add(bst* tree, void* element);

A priori, rien de très différent par rapport au pseudo-code précédent. Et pourtant, le premier argument est un arbre, et non pas un nœud, ce qui signifie que l'on ne va pas pouvoir utiliser la récursivité directement dans la fonction bst_add. Embêtant, non ? Une technique valable dans ce genre de situation est de créer le nœud contenant la nouvelle donnée dans bst_add puis d'ajouter le nouveau nœud dans l'arbre grâce à une fonction récursive avec une signature comme suit :

1

static void bst_add_rec(orderFun compare, bst_node* current, bst_node* new);

Jetons un œil aux arguments de la fonctions bst_add_rec :

• compare : la fonction bst_add_rec va avoir besoin de réaliser des comparaisons pour savoir de quel côté d'un nœud se diriger ; on va donc lui envoyer la relation d'ordre de l'arbre.
• current : ce paramètre désigne la racine de l'arbre (ou du sous-arbre) dans lequel on veut insérer le nouveau nœud.
• new : ici, ce sera le nœud à insérer, qui aura été préalablement créé dans bst_create_node, une simple fonction auxiliaire.

Si tout est clair pour tout le monde, voici l'implémentation des fonctions bst_add et bst_create_node pour commencer :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

void bst_add(bst* tree, void* element) {
  assert(tree);
  assert(element);
  
  // Creating the new node
  bst_node* node = bst_create_node(tree->data_size, element);

  if(tree->root) // If the tree already has a root
      bst_add_rec(tree->compare, tree->root, node); // Start recursion
  else
      tree->root = node; // Setting the new node as the tree's root
}

static bst_node* bst_create_node(int data_size, void* element) {
  bst_node* node = malloc(sizeof(bst_node)); // Allocating a node
  if(!node) {
      perror("malloc");
      exit(EXIT_FAILURE);
  }
  node->data = malloc(data_size); // Allocating data
  if(!(node->data)) {
      perror("malloc");
      exit(EXIT_FAILURE);
  }
  memcpy(node->data, element, data_size); // Setting data
  node->left = NULL;
  node->right = NULL;

  return node;
}

Dans bst_create_node, on alloue de l'espace pour le nœud ainsi que pour la donnée à stocker, on copie la donnée dans l'espace que l'on vient de créer, et on déclare que le nouveau nœud n'a pas de descendants. Vient ensuite un test permettant de vérifier que la racine de tree existe. En effet, s'il s'agit du premier nœud de l'arbre, tree->root vaut NULL, et l'ajout se résume à une simple affectation. Dans le cas contraire, on déclenche la récursivité en insérant le nouveau nœud à partir de la racine déjà existante.

Jetons maintenant un œil à bst_add_rec :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

static void bst_add_rec(orderFun compare, bst_node* current, bst_node* new) {
  if(compare(current->data, new->data) >= 0) { // current >= new
      if(!current->left) // current->left == NULL
          current->left = new;
      else 
          bst_add_rec(compare, current->left, new);
  } else { // current < new
      if(!current->right)
          current->right = new;
      else
          bst_add_rec(compare, current->right, new);
  }
}

La lecture de ce code est plutôt directe : on cherche d'abord à savoir si on se dirige sur la gauche ou la droite du nœud current, puis si le sous-arbre correspondant existe ou non. Si oui, on insère le nouveau nœud dans le sous-arbre par récursivité ; sinon, on ajoute le nœud par affectation.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

/**
 * \brief   Destroys a tree
 *
 * A call to bst_destroy deallocates a tree and all its nodes by calling
 * bst#free. Make sure the program calls it when the tree is not needed anymore.
 *
 * \param   tree    The tree to deallocate
 *
 * \warning     Not using this function to deallocate a bst will cause memory
 * leaks!
 * */
void bst_destroy(bst* tree) {
    assert(tree);
    if(tree->root)
        bst_destroy_rec(tree, tree->root);
    free(tree);
}

static void bst_destroy_rec(bst* tree, bst_node* current) {
    if(current->left)
        bst_destroy_rec(tree, current->left);
    if(current->right)
        bst_destroy_rec(tree, current->right);
    bst_destroy_node(tree, current);
}
static void bst_destroy_node(bst* tree, bst_node* node) {
    if(tree->free) // If the tree has a deallocation function...
        tree->free(node->data); // ... free the node's data dynamic parts
    free(node->data); // Free the node's data slot itself
    free(node); // Free the node
}

Parcours

Jusqu'à présent, nous sommes capables de créer des arbres binaires, et d'y ajouter des données. C'est déjà pas mal, mais il serait autrement plus intéressant de pouvoir exploiter les données stockées dans l'arbre. Nous allons donc écrire une fonction nous permettant de parcourir tous les nœuds de l'arbre et de leur appliquer une procédure⁴ donnée.

Pseudo-code

Ici, rien de plus simple. On va simplement appliquer procedure à tous les nœuds de l'arbre par récursivité :

1
2
3
4
5
6
7
8

Procédure bst_iter (node de type bst_node, procedure de type procédure) :
    Si node est vide
        Quitter la procédure
    Sinon
        bst_iter(node.left, function)
        procedure(node.data)
        bst_iter(node.right, function)
    FinSi

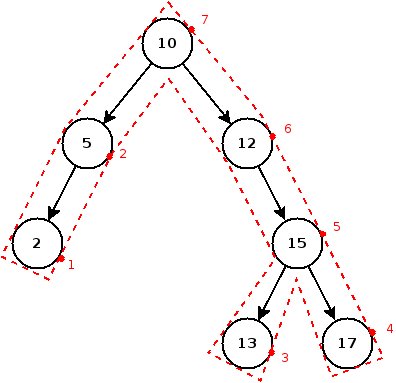
Traversée pre-order, in-order, post-order

Dans le pseudo-code ci-dessus, j'ai arbitrairement choisi de mettre la ligne procedure(node.data) entre l'appel récursif sur le sous-arbre gauche et celui sur le droit. On parle de traversée in-order ; en effet, dans le cas des BST, cette traversée a la particularité de visiter tous les nœuds dans l'ordre, puisqu'on visite d'abord le sous-arbre gauche dont les valeurs sont inférieures, puis le nœud lui-même, et enfin le sous-arbre droit qui contient les nœuds supérieurs.

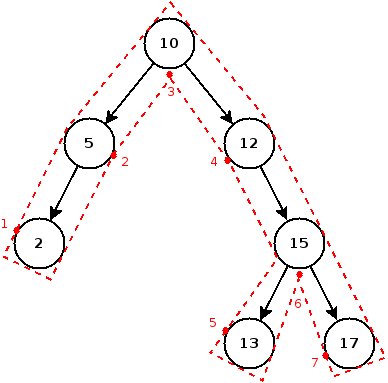
Il existe aussi d'autres types de parcours :

• pre-order : on parcourt d'abord le nœud, puis le sous-arbre gauche, puis le droit.

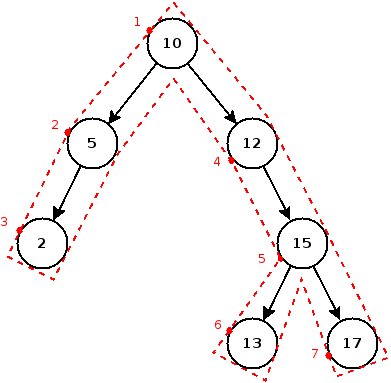
• post-order : on parcourt le sous-arbre gauche, puis le droit, et enfin le nœud.

C

Comme toujours, nous allons devoir utiliser deux fonctions : une fonction pour déclencher la récursivité, et une fonction statique récursive. On définit tout de même le type iterFun par souci de lisibilité : la fonction function doit prendre comme argument un void* (un pointeur sur la donnée) et ne rien retourner.

1

typedef void (*iterFun)(void *);

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

/**
 * \brief     Iterates over a tree
 *
 * Applies a function to every element in the tree.
 *
 * \param     tree    The tree to iterate over
 * \param     function    The function to apply. Cannot be @c NULL.
 *
 * \warning   Breaking any of the above conditions will cause the program to
 * abort!
 */
void bst_iter(bst* tree, iterFun function) {
  assert(tree);
  assert(function);
  if(tree->root)
  bst_iter_rec(tree->root, function);
}

static void bst_iter_rec(bst_node* current, iterFun function) {
  if(!current)
      return;
  bst_iter_rec(current->left, function);
  function(current->data);
  bst_iter_rec(current->right, function);
}

Exemple

Entre la création, la destruction, l'ajout d'un nœud et la traversée, notre petite bibliothèque commence à se remplir. Elle l'est même suffisamment pour écrire un premier programme de test ! Si vous avez bien tout suivi depuis le début, tout devrait vous paraître logique :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

#include <stdlib.h>
#include <stdio.h>
#include "bst.h" // Don't forget that bit

/*
 * Comparison function
 */
int comp(void* a, void* b) {
  return *((int*) a) - *((int*) b); // (a-b)>0 if a>b, <0 otherwise
}

/*
 * Printing function
 */
void print(void* a) {
  printf("%d\t", *((int*) a));
}

int main(int argc, char* argv[]) {
  bst* tree;
  int value = 10;

  printf("Creating tree...\n");
  tree = bst_new(sizeof(int), comp, NULL);
  printf("Done.\n");
  
  printf("Adding %d...\n", value);
  bst_add(tree, &value);

  value = 5;  
  printf("Adding %d...\n", value);
  bst_add(tree, &value);

  value = 12;
  printf("Adding %d...\n", value);
  bst_add(tree, &value);

  value = 15;
  printf("Adding %d...\n", value);
  bst_add(tree, &value);

  value = 17;
  printf("Adding %d...\n", value);
  bst_add(tree, &value);

  value = 13;
  printf("Adding %d...\n", value);
  bst_add(tree, &value);

  printf("Printing data...\n");
  bst_iter(tree, print);
  printf("Done.\n");

  printf("Destroying tree...\n");
  bst_destroy(tree);
  printf("Done.\n");

  return EXIT_SUCCESS;
}

On commence par définir la fonction comp dont l'arbre va avoir besoin pour fonctionner. La syntaxe *((int*) a) - *((int*) b) est un peu surprenante de prime abord, puisqu'on a besoin de déréférencer les arguments préalablement castés en int*, mais en gros, cette fonction ne fait que renvoyer $a-b$, qui sera positif si $a>b$ et négatif si $b>a$. Exactement ce dont notre arbre a besoin. La fonction print quant à elle ne fait qu'afficher le nombre qui lui est envoyé. On utilise cette fonction avec bst_iter pour afficher toutes les valeurs contenues dans l'arbre.

Si tout se passe bien, voici l'affichage que tout un chacun doit obtenir :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

Creating tree...
Done.
Adding 10...
Adding 5...
Adding 2...
Adding 12...
Adding 15...
Adding 17...
Adding 13...
Printing data...
2   5   10  12  13  15  17  Done.
Destroying tree...
Done.

Recherche

Une autre fonction couramment implémentée dans les structures de données permet de rechercher un élément. Dans notre cas, la fonction peut renvoyer le nœud dans lequel l'élément recherché a été trouvé, et une valeur par défaut (notée (nil) dans le pseudo-code) si la valeur n'a pas été trouvée.

Pseudo-code

Comme tout à l'heure avec bst_add, on va utiliser des comparaisons pour savoir si on continue la recherche à gauche ou à droite d'un nœud. Et si d'aventure, un élément n'est ni supérieur ni inférieur, c'est qu'il correspond à l'élément que l'on cherche.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

Fonction bst_search(node de type bst_node, element de type quelconque) :
    Si node est vide
        Renvoyer (nil)
    FinSi
    Si node.data > element
        Renvoyer bst_search(node.left, element)
    Sinon Si node.data < element
        Renvoyer bst_search(node.right, element)
    Sinon
        Renvoyer node
    FinSi

C

A ce stade, vous devriez avoir compris le principe. Nous allons écrire une fonction bst_search qui va simplement s'assurer que l'arbre existe et qui va ensuite déclencher la récursivité à partir de la racine en appelant une fonction récursive bst_search_rec, qui elle va beaucoup ressembler au pseudo-code. Voici ce à quoi cela pourrait ressembler :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

/**
 * \brief     Searches a tree
 *
 * Searches tree for element. A node is considered a result whenever bst#compare
 * returns 0.
 *
 * \param     tree    The tree to search. Cannot be @c NULL.
 * \param     element     The element to search for
 *
 * \return    A pointer to the node element was found, @c NULL if element
 * couldn't be found.
 *
 * \see   bst#compare
 * \see   orderFun
 **/
bst_node* bst_search(bst* tree, void* element) {
  assert(tree);
  if(tree->root)
      return bst_search_rec(compare, tree->root, element);
  return NULL;
}

static bst_node* bst_search_rec(orderFun compare, bst_node* current, void* element) {
  if(!current)
      return NULL;
  if(compare(current->data, element) > 0) // current > element
      return bst_search_rec(compare, current->left, element);
  else if(compare(current->data, element) < 0)  // current < element
      return bst_search_rec(compare, current->right, element);
  else // current == element
      return current;
}

Suppression

La suppression d'un nœud de l'arbre est sans aucun doute l'opération la plus compliquée que nous verrons ici. En effet, la fonction de suppression doit, en plus de supprimer le nœud, faire le nécessaire pour conserver la structure de l'arbre, et c'est loin d'être simple.

Pseudo-code

Lors de la suppression d'un nœud, il y a trois cas différents à considérer :

• Le nœud n'a aucun descendant : pas de problème ici, on peut supprimer le nœud directement.

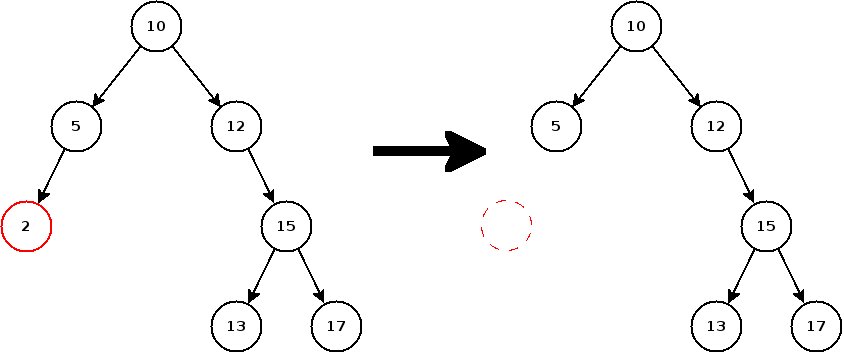
• Le nœud a un descendant (gauche ou droit) : avant de supprimer le nœud, il faut rattacher son père à son descendant. A part ça, tout va bien.

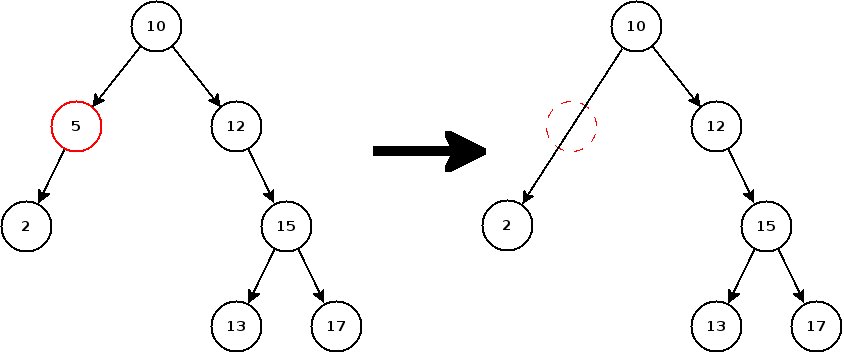
• Le nœud a deux descendants (gauche et droit) : là, c'est la galère. On ne peut pas remplacer le nœud par son fils gauche, car il faudrait replacer tous les nœuds à droite de ce fils de l'autre côté (cf. diagramme ci-dessous), ce qui peut se révéler atrocement long si l'arbre contient ne serait-ce que quelques milliers de nœuds. Dans l'exemple ci-dessus, on pourrait parfaitement essayer de supprimer 10. Cependant, la méthode à employer pour conserver la structure de l'arbre est loin d'être évidente.

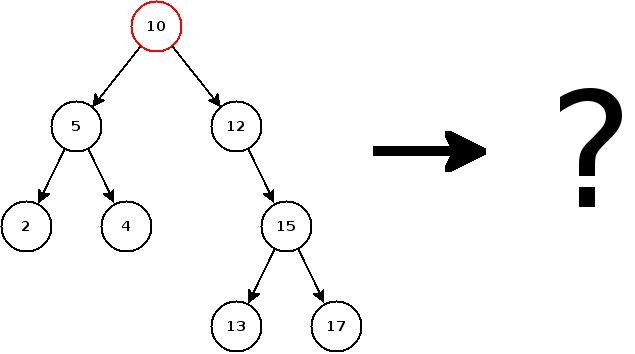
La solution consiste à trouver le successeur du nœud que l'on veut supprimer. Le successeur d'un nœud est en fait le nœud le plus grand (c'est-à-dire le plus à droite) du sous-arbre gauche⁵. En effet, le successeur est par définition le plus grand nœud inférieur à celui qui doit être supprimé, donc on peut remplacer le nœud à supprimer par son successeur, et le tour est joué ! Pour clarifier tout ça, rien ne vaut un bon diagramme :

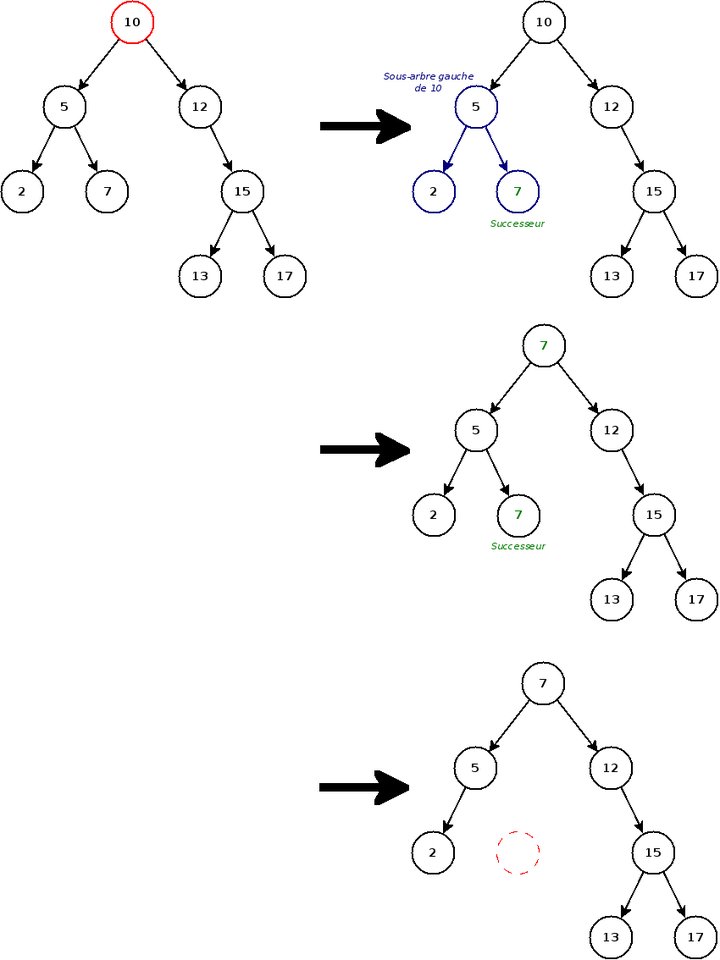
Maintenant, se pose la question de l'algorithme. On décompose la suppression d'un nœud en deux étapes ; premièrement, on recherche le nœud à supprimer, puis on réalise la suppression en elle-même, en fonction du cas dans lequel on se trouve.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

Fonction bst_remove(node de type bst_node, element de type quelconque) :
    Si node est vide
        Renvoyer (nil) // On a pas trouvé d'élément à supprimer
    FinSi
    Si node.data > element
        node.left = bst_remove(node.left, element) // L'élément à supprimer se trouve dans le sous-arbre gauche
    Sinon Si node.data < element
            node.right = bst_search(node.right, element) // L'élément à supprimer se trouve dans le sous-arbre droit
    Sinon // On a trouvé l'élément à supprimer
        Si node.left est vide ET node.right est vide // Aucun fils : Cas n°1
            Renvoyer (nil)
        Sinon Si node.right est vide // Un seul fils à gauche : Cas n°2
            Renvoyer node.left
        Sinon Si node.left est vide // Un seul fils à droite : Cas n°2
            Renvoyer node.right
        Sinon // Un fils à gauche et à droite : Cas n°3
            successor = Max(node.left) // Ou Min(node.right)
            node.data = successor.data
            bst_remove(node.left, successor.data) // On supprime le successeur par récursivité
        FinSi
    FinSi
    Renvoyer node

1
2
3
4
5
6

Fonction Max(node de type bst_node) :
    Si node.right est vide
        Renvoyer node
    Sinon
        Renvoyer Max(node.right)
    FinSi

Vous l'aurez bien compris, cette fonction est de très loin la plus compliquée qu'il vous sera donné d'étudier dans ce cours. En plus de ça, il y a encore un détail qui mérite d'être éclairci. Lorsque l'on supprime un nœud, il faut mettre à jour son père, soit pour le lier au fils du nœud supprimé (cas 2) soit pour lui signaler qu'il n'a plus de fils (cas 1).

Seulement, vous aurez sans doute remarqué que les arêtes sur tous les diagrammes de ce cours sont des flèches : un nœud node connaît ses descendants, node.left et node.right, mais il ne connaît pas son père. Pour palier à cette difficulté, on fait en sorte que la fonction bst_remove renvoie une valeur : la nouvelle racine de l'arbre. Comme ça, la ligne suivante

1

node.left = bst_remove(node.left, element)

permet de mettre à jour node.left en fonction de se qui se passera dans bst_remove(node.left, element).

C

Le pseudo-code de la suppression est assez compliqué, pas vrai ? Ça tombe bien, parce que le C n'apportera aucune difficulté supplémentaire, pour une fois. On doit simplement penser à désallouer l'espace mémoire du nœud que l'on supprime. On peut utiliser la fonction bst_destroy_node évoquée plus tôt.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

void bst_remove(bst* tree, void* element) {
  assert(tree);
  if(tree->root)
      bst_remove_rec(tree, tree->root, element);
}

static bst_node* bst_remove_rec(bst* tree, bst_node* current, void* element) | {
  if(!current)
      return NULL;
  if(tree->compare(current->data, element) > 0)
      current->left = bst_remove_rec(tree, current->left, element);
  else if(tree->compare(current->data, element) < 0)
      current->right = bst_remove_rec(tree, current->right, element);
  else {
      if(!current->left && !current->right) { // No children
          bst_destroy_node(tree, current);
          return NULL;
      }
      else if(!current->right) { // Only a left child
          bst_node* temp = current->left;
          bst_destroy_node(tree, current);
          return temp;
      }
      else if(!current->left) { // Only a right child
          bst_node* temp = current->right;
          bst_destroy_node(tree, current);
          return temp;
      }
      else { // Left and right children
          bst_node* successor = find_max(current->left);
          memcpy(current->data, successor->data, tree->data_size);
          current->left = bst_remove_rec(tree, current->left, successor->data);
      }
  }
  return current;
}

static bst_node* find_max(bst_node* current) {
  if(!current->right)
      return current;
  return find_max(current->right);
}

Et voilà le travail ! On dispose ici d'une interface classique pour gérer des BST depuis n'importe quel type de programme ! Encore une fois, n'hésitez pas à proposer vos travaux, qu'il s'agisse d'implémentations de cette bibliothèque dans le langage de votre choix, une amélioration de celle proposée, ou même un projet qui utilise cette bibliothèque, toutes vos contributions sont les bienvenues !

Inconvénients et évolutions

Déséquilibre et dégénérescence en liste

Malheureusement, les arbres binaires de recherche ne possèdent pas que des avantages¹. Pour s'en rendre compte, il suffit d'imaginer un arbre dans lequel on insère successivement 1, 2, 3, 4 et 5.

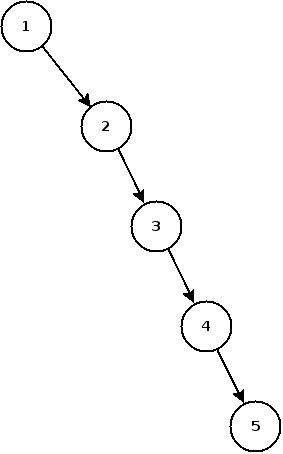
Eh oui, les arbres binaires de recherche sont sensibles à ce que l'on appelle la dégénérescence en liste. Dans l'exemple ci-dessus, on perd tout l'intérêt des arbres puisque l'on est revenu à une autre structure de données (une liste chaînée pour être exact) qui ne bénéficie pas des avantages des arbres.

De manière plus générale, la dégénérescence en liste d'un arbre est un cas extrême de déséquilibre. Un arbre est déséquilibré à partir du moment où un niveau de l'arbre (sauf le dernier) n'est pas rempli.

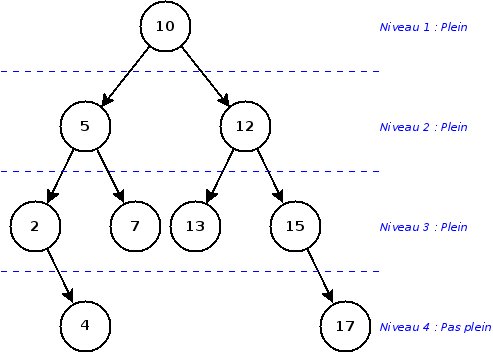
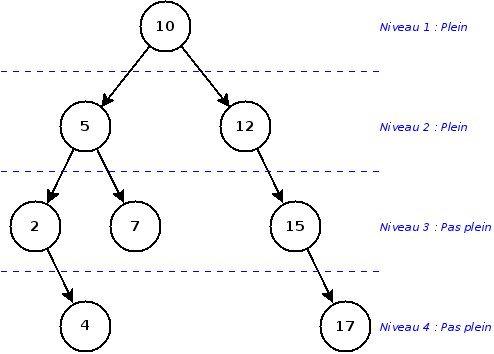
Un déséquilibre provoque un rallongement du temps moyen des opérations, donc on cherche évidemment à éviter cette situation. Malheureusement, avec l'implémentation que nous avons vu durant ce cours, il est difficilement possible de remédier à un tel problème.

Les arbres AVL

En 1962, les algorithmiciens Adelson-Velsky et Landis publient leurs recherches sur une sorte « d'arbre binaire de recherche évolué », que l'on appelle aujourd'hui arbres AVL en référence aux initiales de leurs inventeurs. La différence entre les BST classiques et les arbres AVL est simple : les AVL sont capables de s'auto-équilibrer. Ils préservent donc les qualités des arbres binaires en termes de performances, et les exploitent au maximum puisqu'un AVL n'est jamais déséquilibré.

Cette évolution s'appuie sur une nouvelle opération : la rotation.

À chaque fois que l'on modifie la structure de l'arbre (c'est-à-dire après l'ajout ou la suppression d'un nœud), on doit vérifier si l'opération a déséquilibré l'arbre ou pas. Pour ce faire, on calcule la balance de tous les ancêtres du nœud qui a été modifié, avec la balance définie comme suit :

D'après cette définition, dans un arbre équilibré, toutes les balances sont comprises entre $-1$ et $1$ (inclus). Si la balance d'un nœud sort de cet intervalle, cela signifie que l'on a détecté un déséquilibre. Pour le résoudre, on effectue la rotation comme suit :

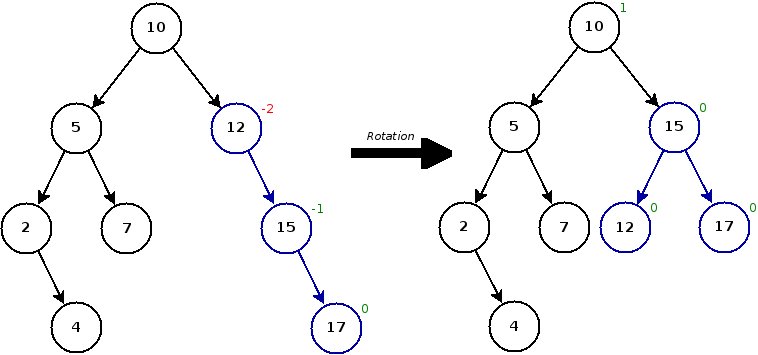
On parvient ainsi à garder un arbre équilibré à tout moment.

Autres évolutions

Les arbres AVL ne sont pas les seules variantes des arbres binaires de recherche. Parmi les autres évolutions des BST, on retrouve notamment les arbres bicolores, les arbres-tas, ou encore les arbres splay. Je vous invite de tout cœur à vous documenter sur ces structures, qui constitueront un excellent complément au cours de vous venez de suivre.

Voilà, ce cours touche à sa fin ; j'espère qu'il vous aura été aussi instructif que possible. Je vous encourage une nouvelle fois à réaliser vous-même l'implémentation des BST dans le langage de votre choix. En plus de mettre en pratique tout ce que vous aurez appris ici, vous participerez à l'établissement d'une petite banque de code permettant à tout un chacun d'aborder ce cours avec son langage privilégié ou avec un langage qu'il souhaite découvrir à travers un exemple concret.

Merci à tous pour votre lecture, et à très bientôt !