Programmation fonctionnelle

Dans ce chapitre, vous allez découvrir une idée qui fait que Haskell est un langage différent de ce que vous avez vu jusqu'à maintenant (en tout cas si vous vous êtes limités à la programmation impérative et orientée objet) : la programmation fonctionnelle.

L'idée est assez simple : à partir d'une fonction de base (l'addition), on peut construire des fonctions plus complexes (calculer la somme des éléments d'une liste, faire une liste contenant la somme des éléments deux à deux de deux listes). Mais souvent, en changeant juste la fonction de base (par exemple par la multiplication), on peut créer d'autres fonctions toutes aussi utiles (calculer le produit des éléments d'une liste, construire une liste contenant le produit des éléments de deux listes deux à deux). Au lieu de répéter le code de ces deux fonctions en changeant juste l'addition en multiplication, pour maximiser la réutilisation du code, on crée des opérations qui à partir d'une fonction créent des fonctions plus complexes. Ainsi, on peut créer une telle opération et lui donner la fonction addition : le résultat sera une fonction qui donne la somme des éléments d'une liste. Mais on peut aussi lui donner la fonction multiplier, et on obtiendra une fonction qui fait le produit des éléments d'une liste.

L'avantage de tout cela, c'est qu'on n'a pas à répéter le code, qu'on peut créer un grand nombre de fonctions à partir de quelques fonctions de base et de transformations simples, et que cela peut rendre la lecture plus claire si on est habitué à ce style de programmation. Enfin, on peut facilement changer les fonctions d'ordre supérieur (les fonctions qui prennent d'autres fonctions comme arguments), pour les optimiser (par exemple permettre de réaliser les calculs sur plusieurs processeurs en parallèle), et toutes les fonctions construites à partir de ces opérations profiteront de ces optimisations.

Exemple : la fonction map

Utilité

Des fonctions qui se ressemblent

Reprenons le code de deux fonctions codées au chapitre précédent :

1
2
3
4
5
6
7
-- ajoute 1 à tous les éléments d'une liste
ajouter1 [] = []
ajouter1 (x:xs) = (x+1):ajouter1 xs

-- multiplie tous les éléments d'une liste par 2
multiplierPar2 [] = []
multiplierPar2 (x:xs) = (2*x):multiplierPar2 xs

Ces deux morceaux de code font des choses similaires et se ressemblent beaucoup : ils transforment chaque élément d'une liste. La ressemblance est encore plus frappante quand on isole la fonction qui est appliquée à chaque élément :

1
2
3
4
5
6
7
ajouter1 [] = []
ajouter1 (x:xs) = f x:ajouter1 xs
    where f x = x + 1

multiplierPar2 [] = []
multiplierPar2 (x:xs) = f x:multiplierPar2 xs
    where f x = 2 * x

À partir de là, vous pourriez vous contenter d'apprendre ce code par coeur (ou de le noter quelque part), et le recopier à chaque fois que vous devez coder une fonction qui applique la même transformation à tous les éléments d'une liste. Cependant, cela crée du code répété et demande trop d'effort. En plus, vous risqueriez de faire des fautes de frappe.

La solution

Pour résoudre ce problème, on va créer une fonction transformerElements qui prend comme arguments la fonction qui sera appliquée à chaque élément, et une liste :

1
2
transformerElements f [] = []
transformerElements f (x:xs) = f x:transformerElements f xs

Maintenant, on peut définir des fonctions et les utiliser avec transformerElements :

1
2
3
4
5
plus1 x = x + 1
fois2 x = 2 * x

ajouter1 xs = transformerElements plus1 xs
fois2 xs = transformerElements fois2 xs

Vous pouvez tester, ces fonctions donnent le même résultat. Si on peut faire ça, c'est qu'en Haskell, les fonctions sont des valeurs comme les autres : on peut prendre une fonction en argument, renvoyer une fonction, les transformer,… En réalité, la fonction transformerElements existe déjà par défaut : c'est la fonction map. Si vous avez le choix entre utiliser la récursivité, ou utiliser directement la fonction map, préférez map : le code est plus court, vous avez moins de chance de faire une erreur en écrivant votre fonction, et n'importe quel programmeur qui lira votre code comprendra immédiatement ce que fait la fonction, alors qu'une fonction récursive est plus difficile à lire, puisqu'il faut suivre le déroulement des appels récursifs. Les fonctions qui prennent des fonctions en argument sont parfois appelées fonctions d'ordre supérieur.

Remarques utiles

Le type de la fonction map

La fonction map a pour type (a -> b) -> [a] -> [b]. Le type du premier argument, a -> b est donc un type de fonction. On le met entre parenthèse, car sinon le type serait interprété comme a -> b -> [a] -> [b], c'est-à-dire le type d'une fonction qui prend trois arguments. Le type de map ne veut pas dire que la fonction qu'on lui donne doit être du type polymorphique a -> b, mais que a et b doivent correspondre respectivement au type des éléments de la liste donnée en argument, et au type des éléments de la liste retournée.

Fonctions anonymes, opérateurs

Les fonctions anonymes sont quelque chose de bien pratique quand on a des fonctions qu'on n'utilisera qu'une seule fois. Par exemple, imaginons que je veuille appliquer la fonction définie par $f(x) = x^2+2x+1$ à tous les éléments de ma liste. Au lieu de définir une fonction qui ne servira qu'une fois, il est possible d'utiliser une fonction anonyme :

1
fonctionLouche liste = map (\x -> x*x + 2*x + 1) liste

L'avantage des fonctions anonymes, c'est que si elles sont courtes et simples, on voit très vite ce qu'elles font. (\x -> x*x + 2*x + 1) est une fonction à un argument, qui correspond à la fonction mathématique f que l'on a vu plus haut. On note une fonction anonyme (\ arg1 arg2 ... argn -> expression ).

Voilà un autre exemple intéressant :

1
ajouter n liste = map (\x -> x+n) liste

Cette fonction ajoute un nombre à chacun des éléments d'une liste. Elle montre une propriété intéressante des fonctions anonymes : elles capturent leur environnement : dans le corps de la fonction anonyme, n désigne le n de l'endroit où la fonction a été définie.

Enfin, il existe une notation spéciale quand on utilise des opérateurs simples appelée la section d'opérateur :

1
2
3
ajouter1 liste = map (+1) liste
multiplierPar2 liste = map (*2) liste
inverser liste = map (1/) liste

Vous remarquez que dans (+1), (*2) et (/1), il y a à chaque fois un "trou", c'est-à-dire qu'il manque un argument à l'opérateur. En fait, cette notation équivaut à la fonction anonyme qui prend un argument, et où l'argument prend la place de ce qui manque. Par exemple, (+1) est équivalent à (\x -> x + 1).

Fonctions sur les listes

Il y a d'autres fonctions très utilisées sur les listes qui, comme map, prennent une fonction comme argument.

Filtrer les éléments

La fonction filter permet de sélectionner seulement certains éléments d'une liste. Elle a pour type (a -> Bool) -> [a] -> [a], et elle renvoie la liste de tous les éléments pour lesquels la fonction renvoie True. Par exemple, on peut s'en servir pour trouver les diviseurs d'un nombre :

1
2
d `divise` n = n `mod` d == 0
diviseurs n = filter (`divise` n) [1..n]

Les fonctions break et span ont toutes les deux pour type (a -> Bool) -> [a] -> ([a],[a]). break coupe la liste au premier endroit où le prédicat (la fonction donnée en argument, qui renvoie un booléen) renvoie True, et renvoie les deux parties. La fonction span coupe la liste en deux parties, la première est le plus long préfixe où tous les éléments respectent le prédicat. Par exemple, on peut se servir de span pour couper une chaîne de caractère comme "47 pommes" en 47 et "pommes" :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
chiffres = ['0'..'9']
lettre = ['a'..'z'] ++ ['A'..'Z']

-- ces fonctions renvoient True si le caractère donné en argument est un chiffre/une lettre
isChiffre car = car `elem` chiffres
isLettre car = car `elem` lettres

-- On doit donner le type, pour que read sache ce qu'il faut essayer de lire
lireNombre :: String -> (Integer,String)
lireNombre xs = let (nombre, suite) = span isChiffre xs in -- vaut ("47"," pommes") si l'entrée est "47 pommes"
                let (_,unite) = break isLettre suite in    -- unite vaut "pommes"
                (read nombre, unite)                       -- (47,"pommes")

En fait, break et span sont presque la même fonction : break retourne le plus long préfixe sur lequel le prédicat renvoie False (puisqu'il coupe dès que le prédicat renvoie True) et le reste de la liste, alors que span retourne le plus long préfixe sur lequel le prédicat renvoie True et le reste de la liste. Il suffit donc d'inverser le prédicat pour passer de break à span.

Comme dans cet exemple, on peut utiliser du filtrage de motif avec let. C'est très pratique pour récupérer des éléments depuis un n-uplet renvoyé par une fonction, mais on ne peut mettre qu'un seul motif possible, donc on ne peut pas faire tout ce qui est faisable avec case.

Il existe aussi des fonctions takeWhile et dropWhile, qui font presque la même chose que take et drop : takeWhile renvoie une liste qui contient tous les éléments jusqu'au premier élément pour lequel le prédicat renvoie faux (c'est donc le premier élément du résultat de span), et dropWhile correspond à l'autre partie de la liste.

N'hésitez pas à essayer de coder votre propre version de toutes ces fonctions, vous en savez assez pour le faire. Vous ne pourrez pas leur donner le même nom que la fonction qui existe déjà dans le Prelude, sinon vous aurez une erreur quand vous essaierez de l'appeler.

fold et scan

foldr, une fonction très générale

Reprenons les fonctions somme et produit du chapitre précédent :

1
2
3
4
5
somme [] = 0
somme (x:xs) = x + somme xs

produit [] = 1
produit (x:xs) = x *  produit xs

Ces deux fonctions ont beaucoup en commun : les seules différences sont que l'on remplace + par * et 0 par 1. On peut donc factoriser les parties communes en une fonction qu'on va appeler reduire, qui prend deux arguments de plus :

1
2
3
4
5
reduire _ n [] = n
reduire f n (x:xs) = f x (reduire f n xs)

somme liste = reduire (+) 0 liste
produit liste = reduire (*) 1 liste

En fait, la fonction reduire existe déjà par défaut : elle s'appelle foldr, et a pour type (a -> b -> b) -> b -> [a] -> b. La fonction fold est en fait une fonction très générale et très puissante, car elle permet de réécrire toutes les fonctions récursives qui parcourent la liste en entier, de la forme suivante :

1
2
f [] = k
f (x:xs) = g x (f xs)

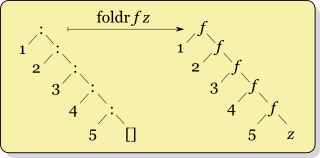Finalement, foldr f n [x,y,z] donne f x (f y (f z n)). Cette idée est illustrée par le schéma ci-contre : foldr f n liste revient à transformer tous les constructeurs : en appels à f, et [] par n. Par exemple foldr (:) [] liste renvoie la liste sans la modifier. C'est donc une transformation très naturelle sur les listes, et très souvent utilisée. Ce type de transformation se généralise très bien sur d'autres structures de données récursives.

Par exemple, on peut recoder la fonction length, avec une fonction qui ignore l'élément et rajoute 1 à la longueur :

1
longueur liste = foldr (\ _ longueurReste -> 1 + longueurReste) 0 liste

Vous pouvez aussi essayer de coder map et filter de cette façon.

foldr est une fonction intéressante à utiliser, parce qu'elle est souvent plus concise que la version où la récursivité est explicite. De plus, elle sera probablement plus claire pour quelqu'un habitué à utiliser foldr. Enfin, foldr donne des informations utiles sur la façon dont la liste sera parcourue; c'est pourquoi il est souvent mieux d'utiliser foldr qu'écrire soi-même la récursivité.

foldl : un fold dans l'autre sens

Maintenant, prenons la fonction renverser :

1
2
3
4
renverser l = renverser' l []

renverser' [] suite = suite
renverser' (x:xs) suite = renverser' xs (x:suite)

On peut réécrire avec la fonction foldl, définie par :

1
2
3
4
5
foldl :: (a -> b -> a) -> a -> [b] -> a
foldl f n [] = n
foldl f n (x:xs) = foldl f (f x n) xs

renverser liste = foldl (\x y -> y:x) [] liste

En utilisant cette fonction, on peut réécrire les versions tail-récursies des fonctions somme et produit :

1
2
3
4
5
6
7
somme liste = somme' 0 liste
somme' s [] = s
somme' s (x:xs) = somme' (x+s) xs

produit liste = produit' 1 liste
produit' p [] = p
produit' p (x:xs) = produit' (x*p) xs

On obtient alors :

1
2
somme liste = foldl (+) 0 liste
produit liste = foldl (*) 1 liste

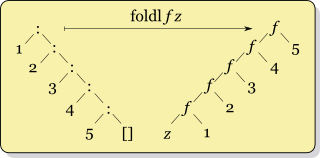Alors que foldr f n [x,y,z] donne f x (f y (f z n)), foldl f n [x,y,z] donne f (f (f n x) y) z : le sens des appels de fonction est donc renversé. Cela correspond au schéma ci-contre. Dans le cas de +, l'ordre d'évaluation ne change rien : ((0+1)+2)+3 donne le même résultat que 1+(2+(3+0)). Cependant, avec certaines opérations, passer de foldr à foldl change le résultat. Par exemple, foldr (:) [] liste renvoie la liste, alors que foldl (\x y -> y:x) [] liste la renverse. Avec la fonction reverse, il faut parcourir toute la liste donnée en argument pour pouvoir renvoyer le premier élément du résultat. C'est la même chose pour la fonction foldl : elle joue mal avec l'évaluation paresseuse. Si vous devez choisir entre deux codes tout aussi clairs, l'un utilisant foldl et l'autre foldr (par exemple, somme liste = foldr (+) 0 liste et somme' liste = foldl (+) 0 liste), le meilleur choix est d'utiliser foldr, qui utilise un modèle de récursivité plus simple à comprendre.

Variantes

Les fonctions foldl et foldr ne nous permettent pas de coder facilement la fonction myMinimum, qui prend le minimum d'une liste. En effet, sans fold, voici la fonction qu'on coderait :

1
2
myMinimum [x] = x
myMinimum (x:xs) = min x (myMinimum xs)

Il existe cependant une fonction foldr1 qui permet de faire cela : le premier élément de la liste est utilisé comme valeur initiale. Son type est (a -> a -> a) -> [a] -> [a]. On a donc :

1
myMinimum liste = foldr1 min liste

Et voilà, c'est aussi simple que ça. Il existe aussi une version de foldl, appelée foldl1 qui joue le même role.

Composer des fonctions

Le sens de la flèche

Ce qu'on aimerait bien faire

Avec les fonctions anonymes, on peut définir des fonctions comme on définirait des variables :

1
2
3
mafonction = (\x y -> blabla)
-- ce code est équivalent à :
mafonction x y = blabla

Si on reprend la fonction map, on remarque qu'on l'utilise très souvent pour définir une fonction qui prend une liste et la donne en argument à map f, où f est une fonction. On va donc essayer de créer une fonction mapF pour factoriser ce code : mapF prend en argument une fonction, et renvoie une fonction qui prend en argument une liste et renvoie la liste transformée avec la fonction

1
2
3
4
5
6
7
foisDeux xs = map (*2) xs
plusUn xs =  map (+1) xs

mapF f = (\xs -> map f xs)
-- on peut redéfinir nos fonctions en utilisant mapF
foisDeux' = mapF (*2)
plusUn' = mapF (+1)

On remarque que l'on n'a plus à mentionner la liste qui est transformée : c'est un style de programmation différent, où au lieu de se concentrer sur les données qu'on prend en argument, manipule et renvoie, on prend un autre point de vue et on crée des transformations (des fonctions) en combinant des fonctions de base avec des fonctions d'ordre supérieur comme mapF. On peut aussi créer les fonctions filterF et foldrF, qui sont les équivalents de filter et foldr :

1
2
3
4
5
filterF p = (\xs -> filter p xs)
foldrF f k = (\xs -> foldr f k xs)

somme = foldrF (+) 0  -- Somme des éléments d'une liste
pairs = filterF even      -- Renvoie tous les éléments pairs

Pour vous exercer, essayez de deviner les types de mapF et filterF :

1
2
mapF :: (a -> b) -> ([a] -> [b])
filterF :: (a -> Bool) -> ([a] -> [a])

L'application partielle

Maintenant que vous avez recodé vos fonctions d'ordre supérieur préférées pour penser en termes de transformations, voilà la bonne nouvelle : vous avez fait tout ça pour rien. En effet, il existe un mécanisme appelé l'application partielle qui permet de ne pas avoir à coder les fonctions mapF, filterF, etc. Prenons la fonction f ci-dessous comme exemple :

1
2
f :: String -> Int -> String
f x n = concat (replicate n x)

Quand on applique la fonction (c'est-à-dire on l'appelle) sans avoir fourni le bon nombre d'arguments, on obtient une fonction qui prend les arguments manquants et renvoie le résultat :

1
2
3
4
5
Prelude> let g = f "NI! "
Prelude> :t g
g :: Int -> String
Prelude> g 5
"NI! NI! NI! NI! NI!"

Ici, en définissant g, on a appliqué partiellement la fonction f, ce qui a donné une fonction qui, quand on lui donne un nombre, affiche ce nombre de fois "NI! ". On se rend compte qu'on peut utiliser l'application partielle pour remplacer mapF :

1
2
3
foisDeux = map (*2)
-- c'est la même chose que :
foisDeux xs = map (*2) xs

On peut faire de même pour filterF et foldrF. Finalement, cela veut dire que quand on a des fonctions définies comme fonction x = f a b c d x, on peut enlever l'argument et se retrouver avec fonction = f a b c d. Par exemple, essayez de réécrire les fonctions suivantes :

1
2
3
4
5
somme xs = foldr (+) 0 xs
produit xs = foldr (*) 1 xs
impairs xs = filter odd xs
plusUn xs = map (+1) xs
listesFoisDeux xss = map (\xs -> map (*2) xs) xss

On obtient :

1
2
3
4
5
somme = foldr (+) 0
produit = foldr (*) 1
impairs = filter odd
plusUn = map (+1)
listesFoisDeux = map (map (*2))

Des fonctions qui renvoient des fonctions

En fait, il n'y a aucune différence entre les fonctions map et mapF. Cela vient en fait de la manière dont l'application partielle fonctionne. Regardons les types et les définitions de map et mapF :

1
2
3
4
5
map :: (a -> b) -> [a] -> [b]
map = (\f xs -> ... )

mapF :: (a -> b) -> ([a] -> [b])
mapF = (\f -> (\xs -> ... ))

La seule différence entre ces deux fonctions est une paire de parenthèses autour de [a] -> [b] et deux fonctions anonymes imbriquées au lieu d'une. Ces deux fonctions seraient donc les mêmes si les fonctions à plusieurs arguments étaient des fonctions qui prennent un argument et renvoient des fonctions à un argument, et ainsi de suite, jusqu'à renvoyer le résultat. C'est exactement ce qui se produit : quand on écrit le type a -> b -> c -> d, il est en réalité compris comme a -> (b -> (c -> d)). De même, quand on écrit une fonction anonyme (\a b c -> quelque chose), c'est comme si on écrivait (\a -> (\b -> (\c -> quelque chose))). Et on a la même chose pour l'application de fonction : au lieu d'écrire ((f a) b) c (c'est-à-dire appliquer la fonction f à a, appliquer la fonction renvoyer à b, puis à c, ce qui donnerait le "quelque chose" de notre fonction définie plus haut), on peut simplement écrire f a b c. Vous pouvez voir que c'est comme ça que fonctionne l'application partielle : quand on donne seulement un argument à une fonction, elle renvoie bien une autre fonction qui prend les arguments restants et renvoie le résultat. On dit que les fonctions sont curryfiées (du nom d'Haskell Curry)

Après ce passage un peu abstrait, nous allons voir quelques applications intéressantes de cette idée.

Quelques fonctions d'ordre supérieur

Quelques fonctions de base

L'opérateur \$ est plutôt utile. Pourtant, sa définition est très simple :

1
f $ x = f x

Cet opérateur correspond donc à l'application de fonction. Cependant, il y a une grosse différence entre les deux : ils n'ont pas la même priorité. On se sert surtout de \$ pour supprimer des parenthèses, comme dans l'exemple suivant (Just est en réalité un constructeur, mais les constructeurs peuvent s'utiliser exactement de la même manière qu'une fonction).

1
2
3
plusMaybe a b = Just (a+b)
-- on peut le remplacer par :
plusMaybe a b = Just $ a + b

\$ a aussi une utilité avec la section d'opérateurs : par exemple, imaginons qu'on ait une liste de fonctions, et qu'on veuille la liste des valeurs renvoyées par chacune de ces fonctions quand on leur donne une valeur en argument :

1
2
3
4
5
fonctions = [(+1),(*2),(3-),(2/),abs]
resultats = map (\f -> f 5) fonctions

-- on peut aussi écrire :
resultats = map ($ 5) fonctions

Une autre fonction parfois utile est la fonction flip. Vous devriez pouvoir deviner ce qu'elle fait simplement avec son type, qui est flip :: (a -> b -> c) -> (b -> a -> c) : la fonction flip renverse les arguments d'une fonction. En fait, on peut aussi noter le type de la fonction comme flip :: (a -> b -> c) -> b -> a -> c. Cela veut dire qu'on peut écrire des choses comme ceci :

1
2
3
4
5
6
reverse = foldl (flip (:)) [] -- Une définition de reverse sans utiliser de fonction anonyme

flipFilter = flip filter -- la fonction filter avec ses arguments renversés
selectEntiers = flipFilter [0..]
-- on peut en fait écrire :
selectEntiers = flip filter [0..]

Mais on peut aussi passer une fonction à plus de deux arguments à flip, et l'effet de flip sera d'inverser les deux premiers arguments (ça se voit très bien en regardant le type). Dans le cas de flip, la curryfication des fonctions est très utile, puisqu'elle permet de ne pas avoir à écrire un flip dépendant du nombre d'arguments de la fonction, et de fournir sans problème un argument à la fonction après avoir appelé flip. Finalement, vous pouvez écrire vous-même une définition pour flip :

1
flip' f a b = f b a

Composer des fonctions

Une fonction très utile (et que vous rencontrerez souvent si vous voulez lire du code) est l'opérateur .. On note f . g la composition des fonctions f et g. Vous avez peut-être déjà rencontré cette opération en maths, notée $f \circ g$. En fait, on a (f . g) x = f (g x). Vous comprendrez mieux comment ça marche avec quelques exemples :

1
2
3
4
5
foisDeux = (*2)
plusUn = (+1)

maFonction x = 2*x+1 -- on peut aussi écrire :
maFonction' = (+1) . (*2)

Maintenant, vous pouvez regarder le type de ., et essayer de comprendre (comme avec flip) comment cet opérateur interagit avec les fonctions qui prennent plus d'un argument.

On peut bien sûr mettre plus de 2 fonctions à la suite :

1
2
3
sommeCarresPairs xs = sum . map (^2) . filter even $ xs
-- on pourrait aussi écrire 
sommeCarresPairs' = sum . map (^2) . filter even

Cette façon d'écrire les fonctions, sans indiquer les arguments, est assez utilisée en Haskell. Dans beaucoup de cas, ça rend le code plus concis, et facile à lire (plus besoin de faire attention aux 3 niveaux de parenthèses imbriquées. Mais dans certains cas, cela peut donner du code complètement illisible, où il est impossible de deviner ce que fait un enchaînement de points. Par exemple, regardons le code suivant, qui teste si un élément est dans une liste :

1
2
3
4
5
6
7
mem x xs = any (== x) xs

-- On transforme ça simplement en :
mem' x = any (==x) -- Cette fonction est encore raisonnablement lisible

-- Mais on peut pousser le style plus loin :
mem'' = any . (==)

Si vous essayez de comprendre comment marche la fonction mem'', vous vous apercevrez qu'elle fait exactement la même chose que la fonction mem. Cependant, cette dernière version est totalement illisible. C'est très pratique pour gagner un concours où il faut un code le plus court possible, mais si vous n'êtes pas dans ce cas, pensez à ceux qui vont relire votre code (vous y compris). Il ne faut surtout pas hésiter à donner des noms à des résultats ou des fonctions intermédiaires pour clarifier le fonctionnement de la fonction. Certains s'amusent à essayer de réécrire (ou d'écrire directement) du code de cette façon. Juste pour l'exemple, voici quelques opérateurs effrayants tirés de la page http://haskell.org/haskellwiki/Pointfree :

1
2
3
owl = ((.)$(.))
dot = ((.).(.))
swing =  flip . (. flip id)

Ce chapitre sur la programmation fonctionnelle est terminée. Les fonctions d'ordre supérieur sont utilisées partout en Haskell, et si vous voyez quelque chose qui se répète, votre premier réflexe doit être de chercher à factoriser le code, parce que moins de code, c'est moins de bugs, et c'est un programme plus facile à comprendre. De plus, cela vous entraînera à appliquer les techniques vues dans ce chapitre. Dans le prochain chapitre, on s'attaque à deux choses très importantes : les types et les classes de types. Alors que jusqu'à maintenant, vous n'avez fait qu'utiliser les types prédéfinis, vous allez apprendre à créer vos propres types, et à les utiliser pour, par exemple, manipuler des opérations mathématiques… et pourquoi pas créer un interpréteur pour un petit langage de programmation ?