L'arbre de Stern-Brocot : énumération des rationnels

Achille Brocot, horloger de son état, introduisit en 1860 un arbre binaire particulier, aujourd’hui appelé « arbre de Stern-Brocot », avec l’aide duquel il souhaitait approximer tout réel par des rationnels aux numérateur et dénominateur limités. Cette restriction lui permettrait d’effectuer l’approximation dans ses horloges, avec des engrenages comportant peu de dents donc simples à fabriquer.

Bien plus tard, en 1999, Calkin et Wilf se basèrent sur cet arbre pour démontrer la dénombrabilité¹ de $\mathbf Q$. En 1999 ? Mais Cantor (Georg Ferdinand Ludwig Philipp de son petit nom, 1845-1918, mathématicien allemand) avait pourtant clos le sujet à la fin du 19^ème siècle. Non sans remous d’ailleurs, puisqu’il paraissait en ces vieux temps aberrant que $\mathbf Q$, dense dans $\mathbf R$, puisse comporter autant d’éléments que $\mathbf N$.

Pour comprendre cette indignation, il faut assimiler la notion de densité d’un ensemble dans un autre. « $\mathbf Q$ dense dans $\mathbf R$ » signifie qu’entre deux réels distincts quelconques, il existe une infinité de rationnels. Par exemple, il existe une infinité de rationnels entre $\sqrt 2$ et $\pi$, entre $0.00011$ et $0.00012$… Notamment, il en existe une infinité entre $0$ et $1$, entre $1$ et $2$, entre $2$ et $3$… ce qui n’a pas empêché Cantor de prouver qu’il y avait autant de nombres rationnels que d’entiers naturels !

Pour suivre cet article, il vous faut être à l’aise avec les ensembles et les fonctions, ainsi qu’avec l’arithmétique, principalement la notion de deux nombres premiers entre eux. Connaître le principe des arbres binaires est aussi nécessaire.

Il est utile de connaître les notions de dénombrabilité et de bijectivité, car elles ne seront que brièvement expliquées. Toutefois, les définitions fournies ici devraient suffire. Maîtriser le principe de récurrence vous permettra de comprendre l’ensemble des démonstrations.

Pour information, l’article est purement mathématique et n’est rattaché à aucune application de la vie courante. Les objectifs sont au nombre de trois :

Vous introduire à la notion de dénombrabilité, avec l’exemple surprenant de $\mathbf Q$ ;
Vous faire découvrir la structure qu’est l’arbre de Stern-Brocot ;
Vous faire manipuler des arbres binaires, notamment au travers de récurrences.

Un ensemble est dit dénombrable s’il comporte autant d’éléments que $\mathbf N$, c’est-à-dire si on peut énumérer ses éléments : le premier, le deuxième, le troisième, etc. ↩

La méthode de Cantor
Dessine-moi un arbre !
Toujours plus loin

La méthode de Cantor

Pour démontrer ce résultat surprenant, Cantor commença par considérer $\mathbf N^2$ comme une grille puis attribuer à chaque point deux coordonnées. Parcourir cette grille selon des diagonales nous permet alors de définir une bijection¹ entre $\mathbf N\times\mathbf N^*$ et $\mathbf Q^+$.

Quadrillage du plan et parcours suivant des diagonales

Plus formellement, pour $n \geq 1$, la $n$^ème diagonale est l’ensemble suivant :

$$ \lbrace (i, j) \in \mathbf N^2, i + j = n \rbrace. $$

En ne conservant que les termes d’indice de colonne non nul et premier avec l’indice de ligne, on définit :

$$E := \lbrace (p, q) \in \mathbf N\times\mathbf N^* \mid \ p \wedge q = 1 \rbrace$$

puis l’application suivante :

$$ f \ \colon \begin{aligned}[t] E &\to \mathbf Q^{+} \\ (p, q) &\mapsto \frac pq \end{aligned} $$

Par définition de $\mathbf Q^{+}$, $f$ est bijective. On a alors successivement :

$\mathbf N\times\mathbf N^{*}$, produit cartésien de deux ensembles dénombrables, est dénombrable ;
$E$, partie infinie d’un tel ensemble, est dénombrable ;
$\mathbf Q^{+}$, en bijection avec $E$, est dénombrable ;
$\mathbf Q^{-}$ est dénombrable par passage aux opposés ;
$\mathbf Q$, réunion de deux ensembles dénombrables, est dénombrable.

Il est donc effectivement possible d’énumérer les rationnels. Seulement, le faire de cette manière ne permet de prévoir simplement ni le n^ème rationnel, ni même le successeur d’un élément donné. Heureusement, Calkin et Wilf parviennent à se servir de l’arbre de Stern-Brocot pour retrouver le résultat de Cantor et pallier ses manques².

Une bijection est une application $f : E \to F$ telle que tout élément de $F$ admette exactement un antécédent par $f$. Autrement dit, une telle application permet de relier un à un les éléments de $E$ à ceux de $F$. $f$ est dite bijective et $E$ et $F$ en bijection. De tels ensembles ont alors même nombre d’éléments. ↩
Ceux du résultat, pas de Cantor. Comprenons-nous bien : ce mec était une machine. ↩

Dessine-moi un arbre !

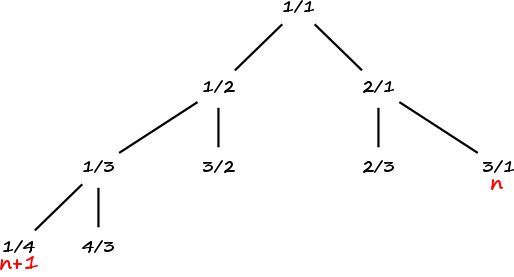
Pour dresser l’arbre de Stern-Brocot, partons de la racine : $\frac 11$. Puis prenons pour fils gauche $\frac{1}{1 + 1}$ et pour fils droit $\frac{1 + 1}{1}$. Plus généralement, on définit le fils gauche d’un noeud $\frac ij$ par $\frac{i}{i + j}$ et le fils droit par $\frac{i + j}{j}$. Ainsi, un noeud $N$ a pour fils gauche $\frac {N}{1+N}$ et pour fils droit $1 + N$. On obtient alors l’arbre suivant :

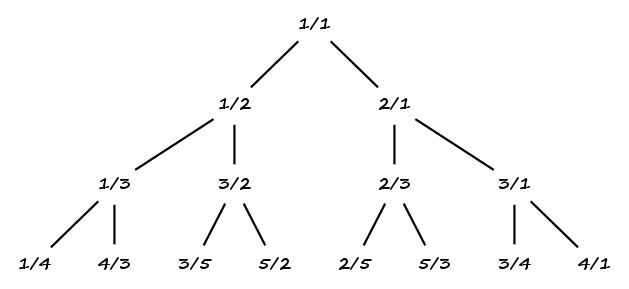
Il est clair que cet arbre ne contient que des rationnels strictement positifs et que $1$ n’apparaît qu’à la racine. En outre, pour tout noeud $N = \frac ij$, on a directement :

$i = j$ i.e. $N = 1$ si le noeud est la racine ;
$i < j$ i.e. $N < 1$ si le noeud est un fils gauche ;
$i > j$ i.e. $N > 1$ si le noeud est un fils droit.

Introduisons maintenant plusieurs résultats dont nous nous servirons par la suite et dont les démonstrations sont intéressantes puisqu’elles constituent des exemples de récurrence sur un arbre binaire¹.

Lemme

Si $\dfrac ij$ est un noeud de l’arbre, $i$ et $j$ sont premiers entre eux.

Démonstration

Le numérateur et le dénominateur de la racine $1/1$ sont clairement premiers entre eux.

Prenons $i/j$ un noeud quelconque de l’arbre, c’est-à-dire $(i, j)$ dans $\mathbf N\times\mathbf N^*$. On a alors :

$$ (i+j) \wedge j = i \wedge (i+j) = i \wedge j. $$

Ainsi, si $i$ et $j$ premiers entre eux, le fils gauche $\frac{i}{i + j}$ du noeud $\frac ij$ la vérifie, de même que le fils droit $\frac{i + j}{j}$.

Par induction structurelle sur le niveau d’exploration de l’arbre, on en déduit le lemme.

Lemme

Deux noeuds $\dfrac ab$ et $\dfrac cd$ ayant des fils gauches (ou droits) identiques vérifient $a = c$ et $b = d$.

Démonstration

Prenons deux noeuds $a/b$ et $c/d$ ayant tous deux pour fils gauche $p/q$.

Par définition :

$$\frac pq = \frac{a}{a+b} = \frac{c}{c+d}.$$

Donc, on a successivement :

$a(c+d) = c(a+b)$
$ac + ad = ac + cb$
$ad = cb$
$a/b = c/d$ car $b, d \neq 0$

Mais ces deux fractions sont irréductibles donc $a = c$ et $b = d$.

On conclut de même dans le cas où les fils droits sont identiques.

Lemme

Pour tout $k \in \mathbf N^*$ et tout noeud $N$ de l’arbre, le noeud provenant d’une suite de $k$ fils gauches du noeud $N$ est $\dfrac{N}{1 + kN}$.

Démonstration

Prenons $N$ un noeud de l’arbre.

Le premier fils gauche de $N$ est son fils gauche $\frac{N}{1 + N} = \frac{N}{1 + 1 \times N}$. Donc on a le résultat pour $k = 1$.

Prenons $k \in \mathbf N^*$ tel que le noeud provenant d’une suite de $k$ fils gauches du noeud $N$ soit $\frac{N}{1 + kN}$.

Alors le fils gauche de ce noeud est :

$$ \dfrac{\dfrac{N}{1 + kN}}{1 + \dfrac{N}{1 + kN}} = \dfrac{N}{1 + kN} \times \dfrac{1}{1 + \dfrac{N}{1 + kN}} = \dfrac{N}{1 + kN + N} = \dfrac{N}{1 + (k+1)N}. $$

Par principe de récurrence, le lemme est vérifié.

Remarque

On conclut de manière analogue que le noeud provenant d’une suite de $k$ fils droits du noeud $N$ est $N + k$.

La bijection promise

Pour établir la dénombrabilité de $\mathbf Q^{+}$, définissons une suite $(v_{n})_{n \in \mathbf N}$ en posant $v_0 = 0$ puis en effectuant un parcours en largeur de l’arbre : niveau par niveau, de gauche à droite.

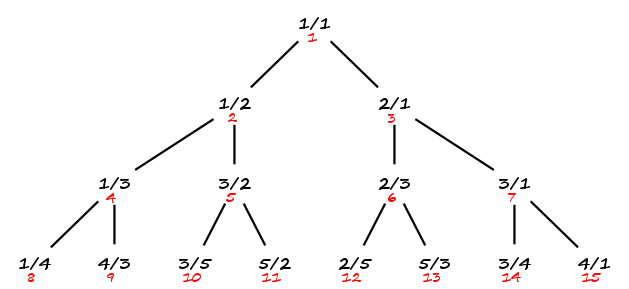
Parcours en largeur de l’arbre, aussi appelé parcours militaire.

Ainsi, $v_{1} = \dfrac 11$, $v_{2} = \dfrac 12$, $v_{3} = \dfrac 21$, $v_{4} = \dfrac 13$, etc.

Cette suite peut paraître sans intérêt de prime abord, et pourtant :

Théorème

La suite $(v_{n})_{n \in \mathbf N}$ est une bijection de $\mathbf N$ dans $\mathbf Q^{+}$.

Démonstration

Tout d’abord, $(v_{n})$ est bien définie sur $\mathbf N$ et à valeurs dans $\mathbf Q^{+}$, par définition de l’arbre. Prouvons maintenant qu’elle est surjective puis injective.

La surjectivité

La surjectivité est équivalente au fait que tout nombre rationnel strictement positif apparaît dans l’arbre. Supposons que ce ne soit pas le cas et, parmi les rationnels strictement positifs n’apparaissant pas dans l’arbre, prenons-en un $\frac pq$ de dénominateur positif minimal.

Comme $1$ est dans l’arbre, $p \neq q$.

Si $p \lt q$, $\frac{p}{q - p}$ a un dénominateur plus petit et positif donc apparaît dans l’arbre. Mais le fils gauche de $\frac{p}{q - p}$ est $\frac{p}{q - p + p} = \frac pq$, ce qui est absurde puisque $\frac pq$ est absent de l’arbre par hypothèse.

On conclut de même dans le cas $p > q$.

L’injectivité

L’injectivité est équivalente au fait qu’aucun nombre rationnel apparaît deux fois dans l’arbre. Par l’absurde, prenons $\frac pq$ apparaissant plusieurs fois dans l’arbre et de dénominateur positif minimal.

Il a été vu plus haut que $1$ n’était présent qu’à la racine, donc $p \neq q$. Si $p \lt q$, on a :

$$ \begin{array}{r c l} & \dfrac{p}{q-p} & \\ \swarrow & & \searrow \\ \dfrac{p}{q} \ \ \ \ & & \ \ \dfrac{q}{q-p} \end{array} $$

Cet arbre sous-entend que $\frac{p}{q-p}$ est le seul père possible pour $\frac pq$. Heureusement, c’est le cas, puisque $\frac{p}{q-p}$ est un père valable pour $\frac pq$ et deux noeuds ayant des fils gauches (ou droits) identiques ont les mêmes numérateur et dénominateur.

Donc, puisque $\frac{q}{q - p} \neq \frac pq$, $\frac pq$ apparaît au moins une fois comme enfant d’un autre noeud, c’est-à-dire que $\frac{p}{q - p}$ apparaît plusieurs fois dans l’arbre, ce qui contredit la minimalité du dénominateur.

On conclut de même dans le cas $p > q$.

On en conclut que $(v_{n})$ est bijective puis que $\mathbf Q^{+}$ est dénombrable et que $\mathbf Q$ l’est.

Nous avons donc retrouvé le résultat de Cantor à l’aide de l’arbre de Stern-Brocot. Il est temps maintenant d’introduire un personnage : Stern.

On parle d’induction structurelle. ↩

Toujours plus loin

Ce que l’on souhaite à présent, ce sont des méthodes pour déterminer facilement le n^ème rationnel dans l’énumération et le successeur d’un rationnel donné. Pour cela, reprenons notre arbre et dressons la liste des numérateurs des noeuds : $1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, 4$… Cette liste forme en fait la suite de Stern¹, introduite en 1858 par Moritz Stern (1807-1894, mathématicien allemand). On notera que la liste des dénominateurs des noeuds forme la suite de Stern privée de son premier terme, ce que nous prouvons plus bas.

Cette suite $(s_{n})$, au nombre de propriétés tout à fait incroyable, est définie comme suit :

$$ \left\{\begin{array}{l} s_0 = 0 \\ s_1 = 1 \\ \forall n \geq 1, s_{2n} = s_{n} \\ \forall n \geq 1, s_{2n+1} = s_{n} + s_{n+1} \end{array}\right. $$

Le théorème suivant nous fournit une expression simple des termes de la suite, lesquels nous permettront par la suite d’obtenir facilement le n^ème rationnel de l’énumération.

Théorème

$$ \forall n \in \mathbf N, s_{n+1} = \sum\limits_{k=0}^{\lfloor \frac n2 \rfloor} \left[\dbinom{n-k}{k} \text{mod} \ 2 \right] $$

où $x \ \text{mod} \ 2$ désigne le reste de la division euclidienne de $x \in \mathbf R$ par $2$. Autrement dit, pour $n \geq 1$, le $n$^ème terme de la suite de Stern est le nombre d’entiers impairs sur la $n$^ème diagonale du triangle de Pascal :

La suite de Stern se lit sur le triangle de Pascal.

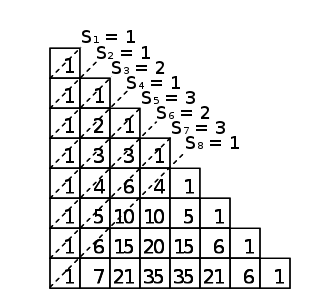
Rationnel à un rang donné

Les termes de la suite de Stern s’avèrent simples à calculer et vont nous permettre de facilement déterminer le rationnel à un rang donné. Commençons par le résultat suivant, important.

Proposition

Si $n = 2m$, $v_{n}$ est le fils gauche de $v_m$. De même, si $n = 2m+1$, alors $v_{n}$ est le fils droit de $v_m$.

$$ \begin{array}{r c l} & v_m & \\ \swarrow & & \searrow \\ v_{2m} \ \ & & v_{2m+1} \end{array} $$

Démonstration

En considérant que la racine est au niveau $0$, on obtient facilement que le $n$^ème niveau de l’arbre comporte $2^n$ éléments et que l’élément le plus à gauche a pour numéro $2^n$.

Prenons alors $m \geq 1$ et notons $N$ le noeud numéroté par $m$ dans notre parcours en largeur. $n$ désignera le niveau auquel se positionne $N$.

Il y a $m - 2^n$ noeuds à gauche et sur le même niveau que $N$ et $2^{n+1} - m$ à sa droite. Chaque noeud à sa gauche ayant deux fils, le fils gauche de $N$ aura pour numéro $m + 2(m - 2^n) + (2^{n+1} - m) = 2m$. Le numéro du fils droit est alors $2m+1$.

On en conclut la proposition.

Ce résultat est notamment utilisé dans le tri par tas et va nous servir à démontrer le théorème suivant, lequel va nous permettre d’exprimer le n^ème rationnel de l’énumération en fonction de termes de la suite de Stern, termes dont nous avons fourni une expression ci-dessus.

Théorème

$$\forall n \in \mathbf N, v_{n} = \dfrac{s_{n}}{s_{n+1}}$$

Démonstration

Tout d’abord $v_{0} = 0 = \frac 01 = \frac{s_{0}}{s_{1}}$ et $v_{1} = 1 = \frac 11 = \frac{s_{1}}{s_{2}}$. Le résultat est donc vérifié pour $n = 0$ et $n = 1$.

Prenons $m$ dans $\mathbf N$ tel que $v_{m} = \frac{s_{m}}{s_{m+1}}$.

Alors, pour $n = 2m$, $v_{n}$ est le fils gauche de $v_{m}$ et on a :

$$v_{n} = \dfrac{s_{m}}{s_{m} + s_{m+1}} = \dfrac{s_{2m}}{s_{2m+1}} = \dfrac{s_{n}}{s_{n+1}}.$$

De même, si $v_{n}$ est le fils droit de $v_{m}$, $n = 2m+1$ et on a :

$$v_{n} = \dfrac{s_{m} + s_{m+1}}{s_{m+1}} = \dfrac{s_{2m+1}}{s_{2(m+1)}} = \dfrac{s_{n}}{s_{n+1}}.$$

Par induction structurelle, on en conclut le théorème.

Successeur d’un rationnel

Le second problème de la méthode de Cantor auquel nous souhaitons remédier est la détermination du successeur d’un rationnel. Le théorème suivant s’avère alors être une aubaine pour nous, puisqu’il fournit une expression de $v_{n+1}$ en fonction de $v_n$.

Théorème

$$\forall n \in \mathbf N, v_{n+1} = f(v_{n}) = \dfrac{1}{1+ 2\lfloor v_{n} \rfloor - v_{n} }$$

Démonstration

On a bien : $f(v_0) = f(0) = 1 = v_1$ et $f(v_1) = f(1) = \frac 12 = v_2$.

Prenons, pour $m \geq 1$, $n = 2m$ pair.

Alors $s_n < s_{n+1}$ car $s_n = s_{2m} = s_m$ et $s_{n+1} = s_m + s_{m+1}$. D’où

$$ f(v_n) = f\left(\dfrac{s_n}{s_{n+1}} \right) = \dfrac{1}{1 + 2\left\lfloor \dfrac{s_n}{s_{n+1}} \right\rfloor - \dfrac{s_n}{s_{n+1}}} = \dfrac{1}{1 - \dfrac{s_n}{s_{n+1}}} = \dfrac{s_{n+1}}{s_{n+1} - s_n} = \dfrac{s_{n+1}}{s_{m+1}} = \dfrac{s_{n+1}}{s_{n+2}} = v_{n+1}. $$

Donc $v_{n+1} = f(v_n)$.

Prenons, pour $m \geq 1$, $n = 2m+1$ impair et supposons que $v_n$ ne soit pas au bord droit de l’arbre.

Alors $v_n$ et $v_{n+1}$ ont un ancêtre commun, noté $v_p$, $k+1$ niveaux au-dessus d’eux, $k \geq 1$, et $v_n$ provient d’une suite de $k$ fils droits du fils gauche de $v_p$ tandis que $v_{n+1}$ d’une suite de $k$ fils gauches du fils droit de $v_p$.

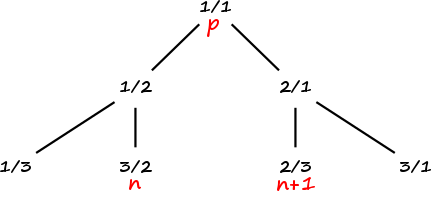
Mais le fils droit d’un noeud $N$ est $1 + N$ et son fils gauche est $\frac{N}{1+N}$.

Donc $v_n = k + \frac{v_p}{1+v_p}$ et $v_{n+1} = \frac{1 + v_p}{1 + k(v_p+1)}$. Mais :

$\dfrac{1 + v_p}{1 + k(v_p+1)} = \dfrac{1}{\dfrac{1}{v_p+1} + k} = \dfrac{1}{1 - \dfrac{v_p}{v_p+1} + k} = \dfrac{1}{1 - v_n + 2k} = \dfrac{1}{1 + 2\lfloor v_n \rfloor - v_n}$.

Donc $v_{n+1} = f(v_n)$.

Prenons, pour $m \geq 1$, $n = 2m+1$ impair et supposons que $v_n$ soit au bord droit de l’arbre.

Notons $k \geq 1$ tel que $v_n$ provienne d’une suite de $k$ fils droits en partant de la racine. Alors $v_{n+1}$ provient d’une suite de $k+1$ fils gauches en partant de la racine.

On a alors $v_n = \lfloor v_n \rfloor = k+1$. Mais $v_{n+1} = \frac{1}{1+(k+1)}$.

Donc $v_{n+1} = f(v_n)$.

En somme, le théorème est vérifié.

Cela est confirmé par l’OEIS. ↩

Nous avons commencé par un résultat surprenant : la dénombrabilité de $\mathbf Q$, suivie de la méthode historique pour démontrer ce résultat. Puis, afin de pallier aux limitations de cette méthode, l’arbre de Stern-Brocot a été introduit. Cela a été l’occasion pour le lecteur d’effectuer des récurrences sur un arbre binaire.

Les curieux pourront consulter les ressources suivantes et se renseigner sur l’incroyable suite qu’est celle de Stern.

Concernant les images et leurs crédits :

Le triangle de Pascal mettant en avant la suite de Stern a été adapté d’ici.
Le logo de l’article provient de Hiteshsaldi, sur Wikicommons. Il est placé sous licence CC BY-SA.
Le reste a été créé pour les besoins de l’article et est placé dans le domaine public.

Un grand merci à Holosmos, Saroupille et Looping pour leur relecture attentive, ainsi qu’à Algue-Rythme, validateur dévoué.

Pour pallier les manques de la méthode historique de Cantor.

La méthode de Cantor

Dessine-moi un arbre !

La bijection promise

Toujours plus loin

Rationnel à un rang donné

Successeur d’un rationnel

8 commentaires

Pas encore membre ?