La phylogénie est la branche de la biologie qui étudie les relations évolutives entre les êtres vivants. Ces relations sont représentées à l’aide d’arbres phylogénétiques, construits à partir de données moléculaires (aujourd'hui) ou morphologiques (avant l'avènement de la biologie moléculaire).
Cet article vise à vous faire découvrir ce qu'est un arbre phylogénétique exactement, ce qu'il représente, et comment on peut les construire.
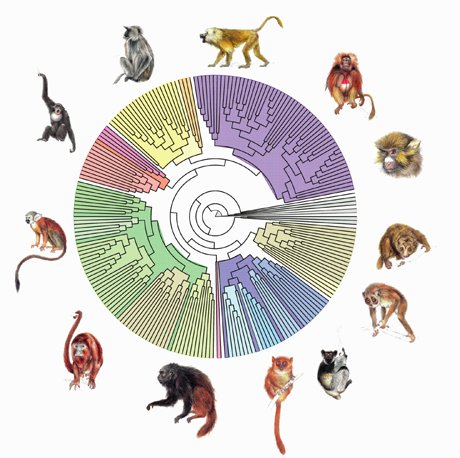
Evolution et sélection naturelle
Un peu d'histoire
L'idée de représenter les relations entre espèces sous forme d'arbre, on la doit essentiellement à Charles Darwin (1809 - 1882), le père de la théorie de l'évolution. Célèbre pour son livre "L'origine des espèces", Darwin a voyagé pendant des années en tant que naturaliste sur un bateau dont le but principal était de cartographier les côtes d'Amérique du Sud. Il observe de nombreuses espèces, ainsi que des fossiles trouvés lors de ses expéditions à terre. Ses observations, notamment à propos des différentes espèces de pinsons qu'on peut trouver sur les îles Galapagos, l'amènent à formuler l'idée que :
- toutes les espèces vivantes dérivent d'un ancêtre commun ;
- et l'évolution des êtres vivants ayant mené à cette diversification est le fruit d'un phénomène qu'il nommera la sélection naturelle.
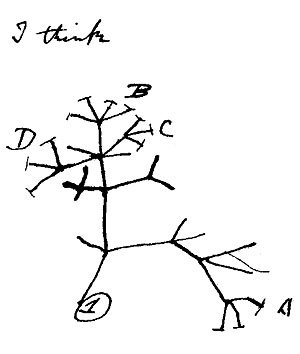
Sélection naturelle et diversification des espèces
Dans une population d'individus d'une même espèce, certaines caractéristiques (physiologiques ou morphologiques) peuvent constituer un avantage reproductif. C'est-à-dire que les individus présentant cette caractéristique auront plus de chance de produire une descendance, ou de produire plus de descendants, que les individus ne présentant pas ce trait particulier.
Si ce trait est héréditaire, au fur et à mesure des générations, la proportion d'individus présentant ce caractère va alors augmenter. Le caractère avantageux est naturellement sélectionné1.
Quelques exemples
- Les ancêtres des girafes ayant le plus long cou pouvaient atteindre des feuilles d'acacia inatteignables par les autres animaux. Mieux nourris, ils vivaient sans doute plus longtemps et avaient donc plus de chances de se reproduire que ceux qui devaient se contenter des feuilles basses, auxquelles plus d'animaux se nourrissaient. De génération en génération, la taille du cou s'est ainsi allongée progressivement pour donner ce que nous connaissons maintenant.
- Certaines espèces d'orchidées présentent des fleurs ayant la forme et l'odeur d'une abeille femelle. L'abeille mâle, attiré, va se poser sur la fleur et la polliniser, permettant sa reproduction. Ce caractère, présentant un avantage reproductif évident, a été naturellement sélectionné et amélioré de génération en génération.
La population évolue ainsi, et si des différences d'évolution apparaissent entre populations d'une même espèce (pour des raisons géographiques par exemple), les différences peuvent devenir telles entre les populations qu'une nouvelle espèce peut apparaître2.
L'exemple typique est celui des pinsons de Darwin. À partir d'une même espèce ancestrale, les populations de pinsons des îles Galapagos ont évolué au cours du temps pour former plus d'une dizaine d'espèces différentes. Chaque espèce étant constituée des descendants d'une population ayant colonisé une des îles. En effet, selon les îles et la végétation qui s'y trouvaient, il était parfois plus avantageux d'avoir un bec fin - adapté à la consommation de la chair et des fleurs de cactus - ou plus intéressant d'avoir un bec épais et solide - sur une île moins pourvue en cactus, mais où se trouvent de nombreuses graines que le pinson casse pour se nourrir.
-
Il existe d'autres mécanismes d'évolution que la sélection naturelle. Citons par exemple la dérive génétique, qui peut se produire lorsqu'un petit nombre d'individus se retrouve séparé de sa population d'origine de manière durable. Si parmi ces individus se trouvaient quelques porteurs d'un caractère héréditaire peu fréquent dans la population initiale, la proportion d'individus ayant ce caractère sera beaucoup plus élevée dans cette nouvelle population isolée, et la probabilité que ce caractère soit transmis aux générations suivantes beaucoup plus grande. On peut ainsi voir émerger des caractères ne procurant aucun avantage reproductif, simplement grâce au hasard. ↩
-
La notion d'espèce est un peu floue. La définition la plus largement acceptée est qu'une espèce est une (ou plusieurs) population(s) d'individus capables de se reproduire entre eux et dont la descendance est viable peut à son tour se reproduire. ↩
Biologie moléculaire
Depuis l'époque de Darwin, de nombreux progrès ont été faits en biologie, et les mécanismes régissant l'évolution sont maintenant bien connus. Voyons donc ce que la génétique et la biologie moléculaire ont révélé.
ADN
Chaque être vivant possède, dans chacune de ses cellules, de l'ADN. Cet ADN est constitué d'une succession de nucléotides. Chaque nucléotide est composé notamment de ce qu'on appelle une base nucléique. Il existe quatre bases nucléiques différentes dans l'ADN :
- l'adénine (A)
- la cytosine (C)
- la thymine (T)
- la guanine (G)
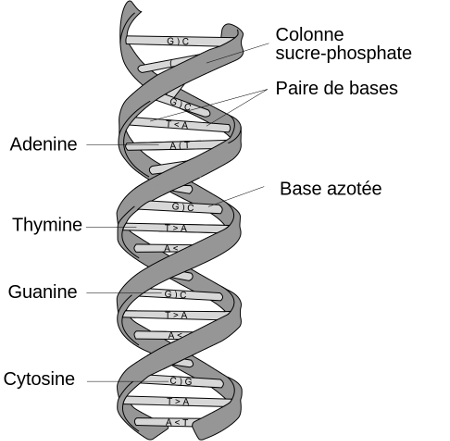
Source : Wikipedia
L'ADN est organisé en deux brins parallèles, formant une espèce d'échelle hélicoïdale. Ces deux brins parallèles sont reliés entre eux par des liaisons chimiques, qui ont toujours lieu entre une adénosine (A) et une thymine (T) ou entre une cytosine (C) et une guanine (G). En face d'un C, on aura donc un G, en face d'un A se trouvera un T (et vice versa).
Cette succession de bases ACTG forme un code, qui va pouvoir être lu par une série de protéines, et est en fait le "plan de construction" de l'organisme en question. Tous les constituants d'un organisme sont créés grâce à cet ADN.
Dans un même organisme, chaque cellule contient, aux erreurs près, le même code ADN. Un être humain est constitué d'environ 1014 cellules (cent mille milliards !), il y a donc 1014 copies du même code ADN dans un être humain.
Chaque fois qu'une cellule se reproduit (croissance de l'organisme, ou tout simplement renouvellement cellulaire), l'ADN est recopié et cette nouvelle molécule d'ADN est encapsulée dans la nouvelle cellule. Étant donné qu'on a deux brins parallèles et complémentaires, on a donc déjà deux copies du code. Lorsque l'ADN doit être recopié, les deux brins sont en fait séparés, et sur chaque brin individuel vont venir se fixer les nucléotides correspondants (donc en face d'un A vient se fixer un nouveau T, en face de chaque C se fixe un G, etc.). On reforme ainsi les brins parallèles, pour finir avec deux doubles brins identiques.
De même, lorsqu'un être vivant donne naissance à un enfant, le code ADN de ce nouvel être vivant est créé en recopiant l'ADN de son, ou ses, parent(s).
- Dans le cas d'une reproduction asexuée (la plupart des organismes unicellulaires, beaucoup de plantes et certains animaux comme le corail), l'ADN du parent est simplement recopié.
- Dans le cas d'une reproduction sexuée, chaque parent va donner la moitié de son ADN, via une cellule d'un type spécifique appelé gamète. Le gamète mâle et le gamète femelle vont alors fusionner, et les deux moitiés d'ADN seront recombinées pour former une nouvelle molécule d'ADN complète, à partir de laquelle l'enfant pourra se développer.
Mutations
Chaque fois que l'ADN est copié, des erreurs peuvent apparaître. Des bases peuvent être mal lues : on aura alors affaire à une substitution. Il arrive aussi qu'une partie de l'ADN soit oubliée lors de la copie, auquel cas il s'agit d'une délétion d'ADN, et enfin, parfois, des bases en trop sont ajoutées, menant à une addition d'ADN. Parfois, des pans entiers d'ADN peuvent également être déplacés d'un endroit à un autre du code.
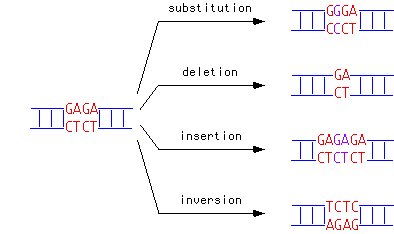
Différents types de mutations (source)
Il existe un mécanisme de correction des erreurs, qui réduit le nombre de celles-ci. Malgré tout, même si les erreurs sont rares, un code ADN est tellement long qu'il en subsiste toujours.
Une bonne partie de ces erreurs sont sans conséquence. Soit parce que la partie de l'ADN affectée ne correspondait à aucun gène (ADN non-codant), soit parce que le gène n'est pas affecté par la mutation, soit encore parce que dans l'environnement où évolue l'individu, le changement provoqué par la mutation n'a aucune incidence sur sa vie (ou sa mort). Mais de temps en temps, la mutation affecte l'individu, et lui donne un avantage ou un désavantage sur les autres individus de la population. En cas de désavantage (handicap, embryon non viable, stérilité, etc.), il aura moins de chances (ou aucune) de se reproduire, et la mutation ne se transmettra pas, ou peu, dans les générations suivantes. Si par contre, cela lui procure un avantage (fût-ce minime), il aura plus de chance de se reproduire, et donc plus de chances de passer cette mutation à ses descendants, qui eux-mêmes seront ainsi avantagés et la mutation pourra se répandre dans la population grâce à la sélection naturelle.
Méthodes d'inférence phylogénétique
Sachant que toutes les espèces d'êtres vivants viennent d'une seule espèce ancestrale, qui a lentement évolué et donné naissance à de nouvelles espèces, chacune des espèces existantes a donc un lien de parenté plus ou moins proche avec les autres. Avec l'inférence phylogénétique, on cherche à connaître ces liens de parenté, représentés sous forme d'un graphe : l'arbre phylogénétique.
Avant l’apport de la biologie moléculaire, les arbres phylogénétiques étaient construits sur base de caractères morphologiques, anatomiques et physiologiques. Dorénavant, grâce notamment aux techniques de séquençage de l’ADN, les arbres phylogénétiques sont construits à partir de séquences génétiques et protéiques. Ce type de données présente plusieurs avantages : pour commencer, les caractères moléculaires sont moins subjectifs et ambigus que les caractères morphologiques. Ensuite, ils permettent d’inférer les relations évolutives entre des organismes très éloignés. De plus, ces caractères évoluent généralement de manière plus régulière et homogène que les caractères morphologiques ou physiologiques. Et enfin, les données moléculaires peuvent être facilement traitées de manière quantitative.
Il existe de nombreuses méthodes, plus ou moins complexes, pour calculer ces arbres à partir de séquences génétiques (ou protéiques). Nous allons maintenant en décortiquer quelques-unes. Les explications se basent sur une inférence à partir de séquence d'ADN, mais les principes sont les mêmes dans le cas de séquences protéiques.
Vocabulaire et structure d'un arbre phylogénétique
Un arbre phylogénétique est donc une représentation graphique des relations de parenté entre des groupes d'êtres vivants. Chaque groupe représente un taxon, ou une unité taxonomique. Généralement, on utilise les espèces biologiques comme taxons de base, mais il est tout à fait possible de construire un arbre phylogénétique de plusieurs sous-populations d'une espèce par exemple.
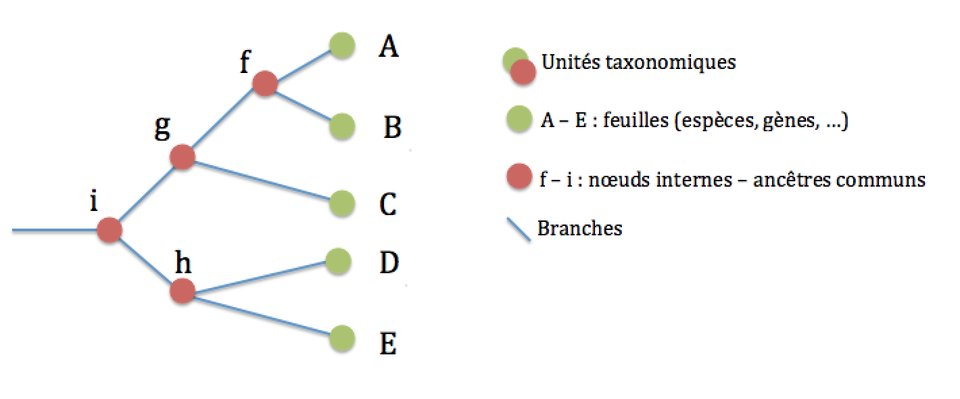
Au départ, on possède des informations sur les feuilles de l'arbre (on connait par exemple tout ou partie du code génétique des espèces concernées), et on veut reconstituer les branches et les noeuds internes à partir de ces informations.
Arbre raciné vs arbre non-raciné
Lorsqu’un arbre est raciné, sa racine représente l’ancêtre commun le plus récent de tous les taxons considérés. Un arbre raciné est donc dirigé, et représente ce qu’on peut appeler un « chemin évolutif », de l’ancêtre commun aux taxons actuels, tandis qu’un arbre non raciné ne donne pas d’indication de direction, mais seulement les relations entre les taxons.
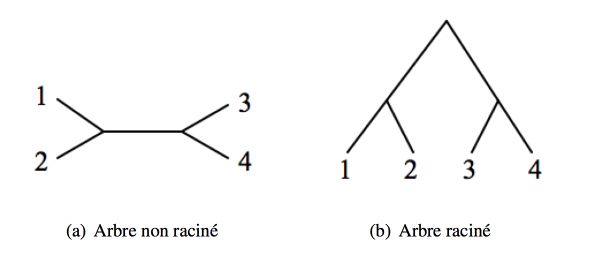
Méthode de distance
Le principe général de ces méthodes est de calculer une distance entre chaque paires d’espèces, pour ensuite trouver l’arbre phylogénétique qui prédit le mieux ces distances.
Mais qu'est-ce que la distance entre deux espèces ? Prenons deux séquences d'ADN :
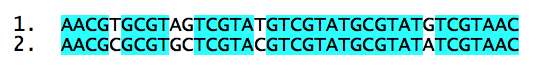
Chaque séquence appartient à une espèce. Ces deux séquences se ressemblent fortement, mais 6 bases diffèrent. On peut prendre, en première approximation, la distance entre séquences comme étant le nombre de mutations nécessaires pour passer de l'une à l'autre. Ces deux séquences seraient donc à une distance de 6.
Il est possible que seules six mutations aient eu lieu entre ces séquences. Il est cependant plus probable qu'il y en a eu plus.
En effet, une base A qui aurait muté en C à un temps t pourrait aussi avoir subi une ou plusieurs autres mutations par la suite.
- Elle peut avoir été retransformée en A : il n'y a alors plus de mutation visible alors que la base en a subi deux (ou plus)
- Ou avoir été mutée en G, par exemple, auquel cas, une seule mutation est visible, alors qu'il y en a eu au moins deux.
Pour prendre cela en compte plusieurs modèles de substitution de l'ADN ont été développés permettant de prendre en compte les possibles mutations successives, indétectables par comptage direct. Ces modèles de substitutions (dont le détail dépasse le cadre de cet article1), aboutissent à une équation permettant de calculer la "vraie" distance entre deux séquences, étant donné le nombre de mutations observées. Par exemple, le modèle le plus simple (le modèle Jukes-Cantor) donne l'équation suivante :
Avec :
- $K$ : le "vrai nombre" de substitutions
- $D$ : le nombre de substitutions observées
- $L$ : la longueur des séquences comparées
Avec nos deux séquences, ayant 6 substitutions observées et une longueur de 38, on a donc $-38\times\frac{3}{4}\ln{(1-\frac{4\times 6}{3\times 38})} \simeq 6,737$ substitutions. Il s'agit d'un nombre théorique, qui représente plutôt une distance corrigée que réellement un nombre de substitutions.
Dans toutes les méthodes d'inférence phylogénétique utilisant la notion de distance entre séquences, on utilise en général un modèle de substitution de l'ADN pour estimer la distance entre deux séquences, à partir du nombre de différences entre séquences.
Exemple : la méthode du Neighbour-joining
Le principe de cette méthode est de joindre itérativement les deux taxons les plus proches, en considérant la distance entre eux, mais également leurs distances respectives aux autres espèces.
Voici un tableau reprenant les distances entre six séquences génétiques, appartenant à six espèces différentes.
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | / | 5 | 4 | 7 | 6 | 8 |
| 2 | 5 | / | 7 | 10 | 9 | 11 |
| 3 | 4 | 7 | / | 7 | 6 | 8 |
| 4 | 7 | 10 | 7 | / | 5 | 9 |
| 5 | 6 | 9 | 6 | 5 | / | 8 |
| 6 | 8 | 11 | 8 | 9 | 8 | / |
Voyons comment on peut en déduire l'arbre phylogénétique des six espèces grâce au Neighbour-joining. On démarre avec un arbre en étoile.
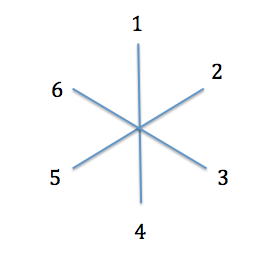
Nous allons calculer une nouvelle matrice des distances, prenant en compte les distances totales d'une espèce avec les autres espèces. Je vous épargne le long développement permettant d'arriver à la formule suivante :
Avec :
- $m_{ij}$, la distance entre $i$ et $j$ dans la nouvelle matrice ;
- $d_{ij}$, la distance de base entre $i$ et $j$ ;
- $N$, le nombre de taxons considérés ;
- et $r_i$, la somme des distances entre $i$ et les autres taxons.
Pour la distance entre les espèces 1 et 2, on a donc :
On fait la même chose pour toutes les paires d'espèces, et on obtient le tableau suivant :
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | / | -13 | -11,5 | -10 | -10 | -9,5 |
| 2 | -13 | / | -11,5 | -10 | -10 | -12,5 |
| 3 | -11,5 | -11,5 | / | -10,5 | -10,5 | -11 |
| 4 | -10 | -10 | -10,5 | / | -13 | -11,5 |
| 5 | -10 | -10 | -10,5 | -13 | / | -11,5 |
| 6 | -9,5 | -12,5 | -11 | -11,5 | -11,5 | / |
On voit tout de suite qu'en prenant en compte la somme des distances d'une espèce par rapport à toutes les autres, on a lissé les différences. Avant, on avait des distances brutes allant de $4$ à $11$. Désormais, on travaille avec des distances corrigées de $-9,5$ à $-13$.
On va regrouper les deux espèces ayant la distance corrigée la plus basse. C'est-à-dire deux espèces qui sont à la fois proches l'une de l'autre (petit $d_{ij}$) et éloignées du reste des espèces (grand $r_i+r_j$). Deux paires d'espèces correspondent à ces critères : 1 et 2, et 4 et 5, qui ont une distance de -13. On choisit une des deux paires (disons 1 et 2), qu'on va donc joindre pour former un taxon.
Quant aux longueurs de branches, on va déterminer la distance entre cet ancêtre commun et les deux espèces qu'on a regroupée grâce aux formules suivantes (soit $a$ et $b$ les deux espèces regroupées, $u$ l'ancêtre commun):
Ce qui donne, pour les espèces $1$ et $2$ concernées :
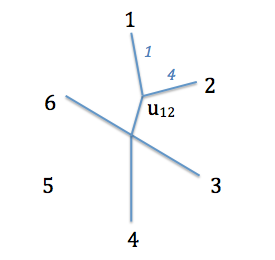
Nouvel arbre obtenu. $U_{12}$ est l'ancêtre commun des espèces $1$ et $2$. En bleu sont données les longueurs de branches connues
On va ensuite pouvoir recommencer les étapes, en considérant cette fois les quatre espèces qui n'ont pas encore été groupées ($3$, $4$, $5$ et $6$), et le nouveau noeud interne ($u_{12}$ ancêtre de $1$ et $2$). Il faut pour cela obtenir les distances entre cet ancêtre et les autres espèces, ce qui est fait simplement en soustrayant les longueurs de branches nouvellement calculées des distances avec les espèces 1 et 2 qu'on avait au départ.
Par exemple, entre l'espèce $3$ et l'espèce $1$, on a une distance de $4$, et entre $1$ et son ancêtre, on a une distance de $1$. Entre $3$ et l'ancêtre $u_{12}$ , on a donc une distance de $4-1 = 3$. On obtient donc le tableau suivant :
| $u_{12}$ | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|
| $u_{12}$ | / | 3 | 6 | 5 | 7 |
| 3 | 3 | / | 7 | 6 | 8 |
| 4 | 6 | 7 | / | 5 | 9 |
| 5 | 5 | 6 | 5 | / | 8 |
| 6 | 7 | 8 | 9 | 8 | / |
On continue ainsi à grouper des taxons deux par deux, jusqu'à ce qu'il ne reste que deux taxons. Au final, on obtient donc un arbre non-raciné complètement résolu, c'est-à-dire qu'aucun noeud n'est le point de jonction de plus de trois branches.
En général, on veut avoir un arbre raciné, afin de connaitre la direction de l'évolution (quelles espèces ont bifurqué en premier, quelles sont les dernières espèces apparues). Pour ce faire, la technique la plus classique est de travailler avec un "outgroup" : une espèce dont on sait qu'elle est extérieure aux autres espèces considérées. C'est-à-dire qu'on sait que l'ancêtre commun de l'outgroup et des espèces considérées est antérieur à l'ancêtre commun de ces espèces. Par exemple, si l'on essaye de construire l'arbre phylogénétique de plusieurs espèces de singes, on peut par exemple ajouter comme outgroup une espèce de félin.
Méthode de parcimonie
Lorsque l’on utilise une méthode de distances, toute l’information à propos d’une séquence est résumée en quelques chiffres (les distances entre la séquence elle-même et les autres séquences utilisées). Il y a donc une grosse perte d’informations. La parcimonie est une méthode basée non plus sur les distances, mais sur les caractères. L’information relative à chaque site de chaque séquence sera utilisée.
Le principe de parcimonie peut être résumé comme ceci : lorsque l’on a le choix entre plusieurs hypothèses, la plus simple doit être favorisée. Appliqué à la phylogénie, cela signifie que l’arbre phylogénétique expliquant les séquences observées en nécessitant le plus petit nombre d’événements évolutifs (mutations, additions, délétions) est considéré comme le « meilleur » arbre. Par exemple, pour construire un arbre phylogénétique à partir des quatre séquences suivantes :
1 2 3 4 | G T T C T T C T C A T T A G A G T T C A T C A T C T T A T A A G A G T C C T T G T T C C A A T A A G A G T T G T T C T A C T A A T T A G A G T A |
On considère chaque caractère séparément et on construit tous les arbres possibles. Donc, pour le premier caractère (GCCG), on construit les trois arbres (non racinés) possibles. Pour chacun de ces arbres, on compte le nombre d’événements évolutifs nécessaires au minimum pour expliquer les données de ce site.
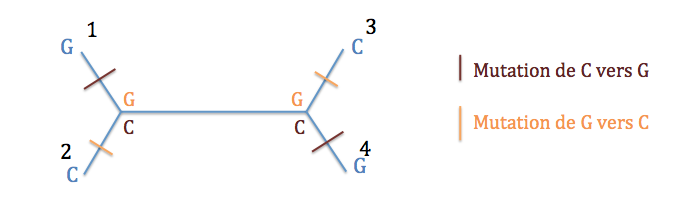
Typologie 1 : deux possibilités, soit les noeuds internes sont G, et il y a eu deux mutations de G vers C, soit les noeuds internes sont C et il y a eu deux mutations de C vers G. On a donc minimum deux événements évolutifs.
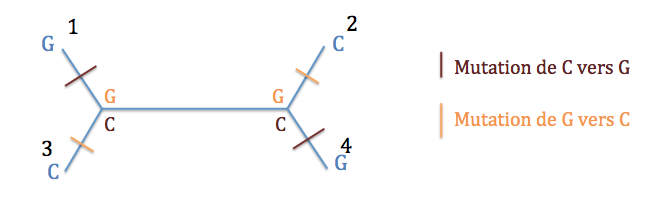
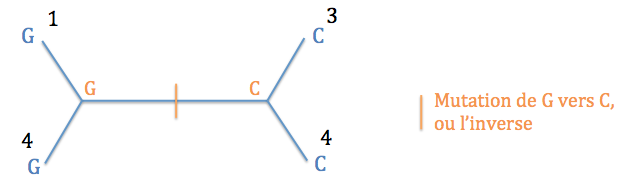
Typologie 3 : l'ancêtre des espèces 1 et 4 présentait un G et l'ancêtre des espèces 2 et 3, un C. Il y a donc eu une mutation de C vers G ou l'inverse entre les deux noeuds internes. Un seul événement évolutif suffit.
On refait ensuite la même chose pour chaque caractère, et on obtient la table suivante.
| Position | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | Somme |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Topologie 1 | 2 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 13 |
| Topologie 2 | 2 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 2 | 13 |
| Topologie 3 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 2 | 11 |
Au total, la topologie 3 requiert donc moins d’événements évolutifs que les topologies 1 et 2, et sera donc choisie. Cependant, si cette méthode tient compte de chaque caractère individuellement, elle ne permet de choisir qu’entre différentes topologies. Or, un arbre phylogénétique n’est pas seulement défini par sa topologie, mais également par des longueurs de branches.
Maximum de vraisemblance
Les méthodes utilisant le maximum de vraisemblance tiennent également compte de la longueur des branches de l’arbre phylogénétique, en plus d’être basées sur les caractères.
Principe
Il s’agit, pour ces méthodes, de comparer un grand nombre d’arbres phylogénétiques possibles (topologie et longueurs des branches). L’arbre choisi sera celui qui maximise la probabilité d’observer les données utilisées, étant donné un modèle de substitution de l’ADN. Cette probabilité est appelée « vraisemblance » de l’arbre phylogénétique.
Avec : - $T$ un arbre possible - $L$ la vraisemblance de l’arbre $T$ - $D$ les données observées - $\gamma$ un modèle de substitution de l’ADN
On veut donc trouver l’arbre phylogénétique, défini par sa topologie et les longueurs de ses branches, ayant la plus haute vraisemblance.
Probleme NP-complet
Pour ce faire, il faudrait en principe construire tous les arbres possibles et comparer leur vraisemblance. Malheureusement, la détection, parmi tous les arbres possibles, de l’arbre de plus haute vraisemblance est un problème dit « NP-dur », c’est-à-dire qu’aucun algorithme connu ne peut résoudre ce problème en un temps raisonnable. En effet, le nombre de topologies possibles pour un arbre phylogénétique non raciné de $t$ augmente de façon exponentielle lorsque $t$ augmente, et peut être calculé grâce à la formule suivante :
Ce qu’il faudrait encore multiplier par toutes les longueurs de branches possibles pour obtenir le nombre total d’arbres possibles. Par conséquent, il est impossible de tester chacun des arbres possibles.
On utilise donc des heuristiques, c’est-à-dire des algorithmes qui vont explorer une partie de l’espace des solutions en se concentrant principalement sur les parties « prometteuses ». Ces algorithmes permettent de trouver, en un temps polynomial, une bonne solution. Ils ne peuvent cependant pas garantir que la solution trouvée est la solution optimale. En effet, l’espace des solutions peut contenir de nombreux pics (régions de solutions de haute vraisemblance), séparés par de grandes vallées (régions de solutions de basse vraisemblance), et lorsque l’on s’arrête en haut d’un pic, même si les solutions environnantes paraissent moins bonnes, il est impossible de savoir avec certitude qu’aucun pic plus haut ne se trouve à quelques vallées de là. Les méthodes de maximum de vraisemblances donnent de meilleurs résultats que les méthodes de distances et de parcimonie et présentent comme avantage d’avoir un cadre statistique consistant, permettant de comparer facilement les hypothèses. La contrepartie de cela étant bien sûr un temps de calcul bien plus élevé que ces deux méthodes.
Hill-Climbing et Recuit Simulé
Le Hill-Climbing est la méthode heuristique la plus simple : on construit un arbre initial (avec une topologie, des longueurs de branches, et des paramètres du modèle de substitution ADN choisi), grâce à une méthode de distance par exemple, et on optimise ensuite la longueur de ses branches. On modifie alors la topologie de cet arbre, et on réoptimise les longueurs de branches. Si ce nouvel arbre a une vraisemblance supérieure à l’arbre initial, ce dernier est abandonné et remplacé par le nouveau. Et on recommence le processus : modification, optimisation, comparaison, conservation du meilleur arbre, jusqu’à ce qu’aucune modification de la solution courante ne puisse améliorer celui-ci.
1 2 3 4 5 6 7 8 9 10 11 | meilleurArbre = methodeDistance(donnees) //ou parcimonie
optimisationDesBranches(meilleurArbre)
while (on peut trouver une modification de la topologie qui améliore meilleurArbre) do
nouvelArbre = modificationTopologie(meilleurArbre)
optimisationDesBranches(nouvelArbre)
if vraisemblance(nouvelArbre, donnees) > vraisemblance(meilleurArbre, donnees) then
meilleurArbre = nouvelArbre
end if
end while
|
À chaque étape de l’algorithme, on optimise donc les longueurs de branches de l’arbre considéré. De ce fait, l’algorithme atteint un optimum en peu d’étapes, et est donc très rapide. Par contre, beaucoup de calculs sont faits pour optimiser des arbres phylogénétiques qui seront rejetés tout de suite après car moins bons que l’arbre précédent. Un autre désavantage de cet algorithme est qu’en n’acceptant uniquement les changements qui améliorent l’arbre phylogénétique, on n’explore l’espace des solutions que très localement. Par conséquent, on reste bloqué dans un optimum local, qui peut être beaucoup moins bon que l’optimum global.
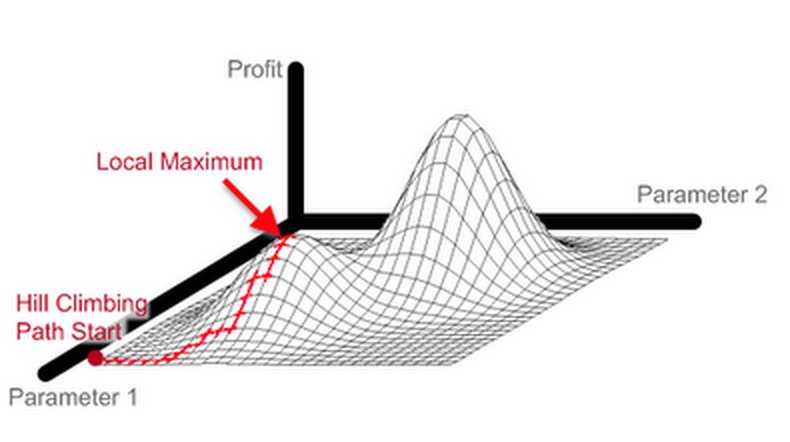
Hill-Climbing - Illustration de l'espace des solutions. Source
L’algorithme de Recuit Simulé tombe moins facilement dans des optima locaux que le Hill-climbing en permettant la sélection régulière d’une solution moins bonne que la solution courante. Le nom de recuit simulé (en anglais « simulated annealing ») vient de la thermodynamique et fait référence à la cristallisation de certains liquides et métaux.
Lorsque l’on refroidit une substance en vue d’obtenir un cristal, cette substance est au départ dans un état non-ordonné, avec une haute énergie libre. Au fur et à mesure que la température diminue, les molécules s’ordonnent et s’alignent. Lorsqu’elles sont complètement alignées, et forment donc un cristal, la substance a atteint un état d’énergie minimale. Cependant, si la température décroît trop rapidement, certaines molécules peuvent être figées dans des positions non-optimales, et le cristal présentera des défauts (ou la substance ne cristallisera pas du tout). Il est donc essentiel de diminuer la température très lentement et par paliers (ce processus est alors appelé « annealing »), afin de laisser le temps aux molécules de se mettre en place.
L’algorithme de recuit simulé est basé sur un principe similaire. On veut atteindre une solution optimale, c’est-à-dire de vraisemblance maximale (correspondant à une énergie minimale). Pour ce faire, on modifie la solution en permettant éventuellement des changements qui n’améliorent pas immédiatement la solution. C’est-à-dire qu’à la différence du Hill-Climbing, où l’on n’accepte que les modifications qui améliorent la solution, les solutions de vraisemblance inférieure à la solution courante seront acceptées avec une certaine probabilité. Et cette probabilité est proportionnelle à une variable nommée « température », qui est haute au début de l’algorithme et descend ensuite par paliers.
Ainsi, au départ, la probabilité d’accepter une « moins bonne » solution sera très grande, et au fur et à mesure des itérations de l’algorithme, cette probabilité diminuera. De ce fait, il sera possible de traverser des « vallées » de l’espace des solutions, alors que le Hill-Climbing ne peut que grimper une colline (la première qu’il rencontre).
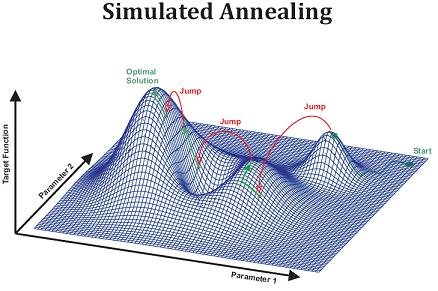
Recuit simulé - Illustration de l'espace des solutions. Source
Par ailleurs, l’algorithme de recuit simulé ne fait plus une optimisation « intra-step » (optimisation des longueurs de branches à chaque itération, avant la comparaison avec la meilleure solution courante) mais bien une optimisation inter-step. À chaque itération, il y a modification à la fois de la topologie et/ou de la longueur des branches, et on n’optimise plus la longueur des branches avant de comparer le nouvel arbre à l’arbre courant. On évite ainsi de longs calculs sur des arbres qui seront rejetés.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | meilleurArbre = methodeDistance(donnees) //ou parcimonie
while (on peut trouver une modification qui améliore meilleurArbre) do
nouvelArbre = modificationTopologieOuBranches(meilleurArbre)
if vraisemblance(nouvelArbre, donnees) > vraisemblance(meilleurArbre, donnees) then
meilleurArbre = nouvelArbre
else
p = probabiliteConserverArbre(temperature)
if nombreAuHasard < p then //nombre entre 0 et 1
meilleurArbre = nouvelArbre
end if
end if
end while
|
Algorithme génétiques
Un Algorithme Génétique (GA) est un algorithme heuristique qui s’inspire des mécanismes de l’évolution biologique : mutations, sélection des individus les plus aptes, reproduction avec recombinaison.
On commence par générer plusieurs arbres phylogénétiques (dont on définit la topologie, la longueur des branches ainsi que les paramètres du modèle de substitution ADN choisi), pour former une population de solutions (la génération 0). Chaque individu de cette population est alors évalué grâce à une fonction de fitness. Dans le cas présent, la fitness est bien sûr proportionnelle à la vraisemblance de l’arbre (on utilise en général le logarithme de la vraisemblance).
On va alors créer une nouvelle population de solutions à partir de la génération 0 : les individus ayant les meilleurs fitness sont sélectionnés pour être les « parents » de la génération suivante. Ils sont alors recombinés entre eux (typiquement deux par deux) pour former de nouveaux individus. Pour terminer, ces individus subissent des mutations au hasard. La nouvelle population est alors à son tour évaluée, et l’on continue itérativement à créer de nouvelles générations. Comme les individus de la génération n sont formés à partir des « meilleurs » individus de la génération n−1, la fitness moyenne des individus augmente de génération en génération jusqu’à atteindre un optimum, qu’on espère global.
Utiliser un algorithme génétique pour l'inférence phylogénétique revient donc à utiliser les principes de la théorie de l'évolution pour avoir des informations sur l'évolution des espèces biologiques2.
Il existe de nombreuses variantes des algorithmes génétiques, et ce, pour chaque étape de l’algorithme. La sélection peut se faire par exemple de manière stricte (on prend les x meilleurs individus) ou stochastique (la probabilité qu’a un individu de se reproduire est proportionnelle à sa fitness) ; la recombinaison peut se faire de diverses manières ; les conditions d’arrêts peuvent également varier (arrêt après un certain temps, un certain nombre d’itérations, un certain nombre d’itérations sans amélioration de la fitness…).
Une variante sympa : l'algorithme génétique métapopulationnel
Plusieurs populations d’arbres phylogénétiques sont générées, et à chacune de ces populations va être appliqué un algorithme génétique. L’intérêt d’avoir plusieurs populations évoluant en parallèle, est qu’on peut faire interagir ces populations, en appliquant le « Consensus Pruning » : toutes les x générations (x étant défini à l’avance, ou un nombre tiré au hasard), on prend le « meilleur » arbre de chaque population, et on compare ces arbres, afin de voir s’ils ont des branches en commun. Si une branche se retrouve dans toutes les populations, elle est fixée, et les mutations appliquées à chaque génération d’arbres ne peuvent la modifier. Le Consensus Pruning permet d’appliquer une forte sélection aux populations, sans risquer de se retrouver bloqué rapidement dans un optimum local. En effet, la probabilité que plusieurs populations parviennent au même optimum local est très faible (et diminue bien sûr avec le nombre de populations).
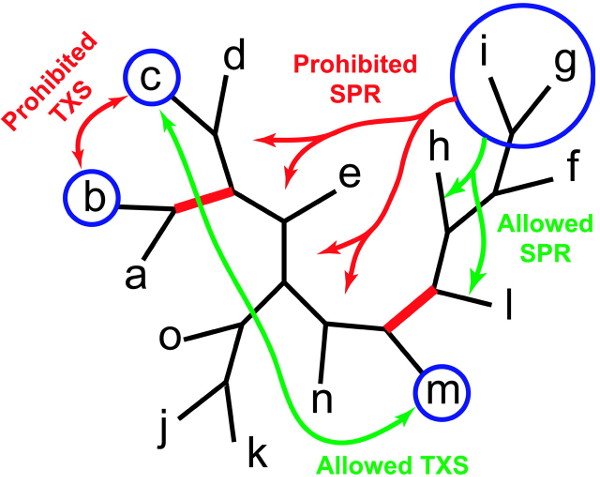
Algorithme génétique métapopulationnel - Consensus pruning : deux branches sont fixées, celle qui regroupe a et b, et celle qui regroupe f, g, h, i et l. Certains changements de topologies sont donc interdits (en rouge) et d'autres restent autorisés (en vert).
-
Certains modèles de substitutions de l'ADN sont très complexes, et prennent de nombreux paramètres en compte, comme par exemple, l'hétérogénéité du taux de substitutions des séquences ADN (certaines parties de l'ADN sont plus susceptibles de présenter des mutations que d'autres), des taux de substitutions différents selon la base de départ et la base d'arrivée, etc. ↩
-
Et ça, c'est beau ! ↩
Grâce aux progrès technologiques récents, de plus en plus d'espèces voient leur ADN complètement séquencé, et le nombre de séquences disponibles dans les bases de données scientifiques publiques croît de manière exponentielle. En parallèle, les ordinateurs voient leur puissance de calcul augmenter. Il est donc de plus en plus facile de construire des arbres phylogénétiques extrêmement vraisemblables, y compris sur un grand nombre d'espèces différentes. Les données sont plus nombreuses et plus fiables, et l'on peut utiliser des algorithmes complexes et de modèles de mutation les plus proches possible de la réalité puisqu'on n'est beaucoup moins limité par les capacités des ordinateurs.
Avoir des informations précises sur le déroulement de l'évolution naturel est évidemment intéressant, mais la reconstruction d'arbres phylogénétiques peut également avoir des applications pratiques. Par exemple, en biologie de la conservation, on se sert fréquemment des arbres phylogénétiques pour savoir quelques espèces ou populations doivent être prioritairement sauvées de l'extinction. La phylogénie peut également permettre d'avoir des informations sur l'émergence et l'évolution d'un agent pathogène, et ainsi donner des solutions pour éradiquer celui-ci, ou réduire le risque d'infection.