Vous avez sûrement déjà apposé à un chèque, un formulaire ou même votre carte d'identité ce gribouillis, tirant pour certains de la calligraphie qu'on appelle "signature".
La signature est un élément très important car elle permet d'assurer qu'une action administrative ou juridique a été réalisée par la personne qui prétend l'avoir réalisée.
Aujourd'hui, cependant, de plus en plus de documents n'ont aucun support physique, les factures elles-mêmes peuvent se contenter d'être un simple document PDF1. Le besoin de s'assurer que la personne émettant cette facture est bien celle qu'elle prétend être reste toujours d'actualité2, mais comment signer un document qui n'est pas couché sur papier ?
-
À condition d'être acceptée préalablement par l'acheteur, une facture peut être émise par voie électronique et non sur support papier. Elle tient lieu de facture d'origine. vos-droit.fr ↩
-
Outre de grandes entreprises qui ont été lestées de plusieurs millions d'euros, des particuliers se voient envoyer des fausses factures. ↩
- Une question de communication
- Une histoire de digestion
- Assurer l'intégrité du document et de l'acte
- Tout en assurant l'authenticité.
- Le mot de la fin
- Sources
Une question de communication
Comme la question de la signature est fortement liée à celle de la fraude, la question de la sécurité sera centrale. Et lorsque l'on parle de sécurité, il est toujours bon de savoir de quoi l'on parle pour savoir ce qu'on veut sécuriser.
La grande question à se poser sera alors : pourquoi avons-nous besoin d'une signature ?
Il est important de comprendre un concept fondamental dans notre situation : celui d'une communication entre deux entités. Cette communication a été très simplement schématisée par Shannon1 : elle met en relation un émetteur et un récepteur via un canal qui peut être parasité. Nous pourrons ajouter que ce canal peut être écouté par une personne à qui n'est pas destiné le message.
La personne qui reçoit le message s'appelle Ze Zeste, l'émetteur s'appelle Clem, et c'est Cornichon2 qui jouera le rôle du méchant3  .
.
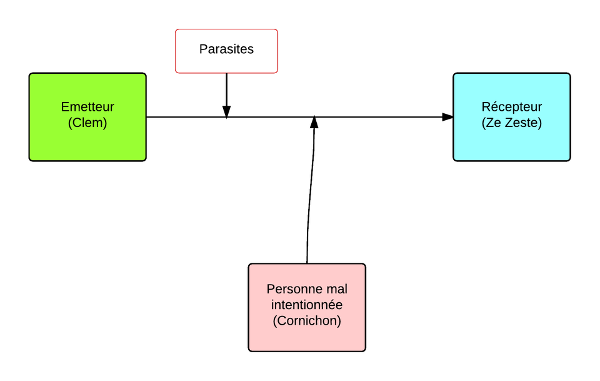
Dans le cadre de ce qui nous intéresse, on distingue trois grandes notions en ce qui concerne le message :
- L'intégrité : le message que reçoit Ze Zeste doit être celui émis par Clem
- La confidentialité : le message que reçoit Ze Zeste ne doit être lisible que par lui
- L'authenticité : Ze Zeste doit être sûr que c'est bien Clem qui a envoyé le message et pas Cornichon qui se prend pour Clem.
La signature en soi ne va s'occuper (la plupart du temps) que de l'intégrité et de l'authenticité du message.
L'article 1316 du code civil4 définit la signature électronique comme l’usage d’un procédé fiable d’identification garantissant son lien avec l’acte auquel elle s’attache.
Revenons quelques secondes à la signature sur un document papier. Dans un monde parfait, chaque signature est unique et donc signer c'est bel et bien s'assurer que le signataire est celui qu'il prétend être.
De plus, par divers procédés, allant du cachet de la Poste (encore une signature tiens  ), au duplicata envoyé à soi-même, on peut réussir à s'assurer que la signature a été apposée sur un document authentique.
), au duplicata envoyé à soi-même, on peut réussir à s'assurer que la signature a été apposée sur un document authentique.
L'analogie ne s'arrête pas là ! Pour apposer votre signature, il faut que le document réserve un espace blanc à cette dernière. Et il ne faut pas avoir une signature trop grosse sous peine d'écrire sur la table.
Pour un document électronique, c'est pareil. Le seul problème pour un document électronique, c'est que plus il est gros et plus il risque d'y avoir des erreurs dans sa transmission. Du coup si la signature prend trop de place, cette fois-ci on augmente le risque que le document reçu soit différent de celui émis5, dommage.
C'est pourquoi, pour créer une signature électronique, les créateurs de logiciels ont décidé de s'inspirer de ce qu'on appelle un algorithme de hachage.
-
Sa biographie. ↩
-
Pour connaître toute l'histoire. ↩
-
Dans la littérature, vous entendrez surtout parler de Alice (Expéditeur), Bob (Destinataire) et Eve (Homme dans le milieu). ↩
-
C'est l'article qui définit les usages légaux de documents électroniques. ↩
-
Et ce malgré la mise en place de codes correcteurs. ↩
Une histoire de digestion
Certains auront peut-être détecté un jeu de mots dans ce titre, pour la simple et bonne raison que les anglophones ont tendance à appeler le résultat d'un algorithme de hachage un digest (ou hash).
L'idée de ces algorithmes est au départ de générer une structure de données qui certes peut prendre un peu d'espace en mémoire, mais qui aura des temps d'accès constants1. La représentation la plus simple de cette structure appelée table de hachage (ou HashTable) est le tableau avec un titre à chaque colonne.
Le principe de cette table, c'est de faire un tableau plein de vide, où les données ne seront pas très nombreuses. Mais elles seront placées d'une manière "spéciale". En fait pour ranger ces données, plutôt que de demander la case n°42 par exemple, vous allez demander la case "clémentine". Et le mot clémentine va être passé dans un algorithme de hachage qui va le transformer en un nombre qui représente le numéro de la case recherché. Du coup pour chercher la case "clémentine", seul le temps pris par l'algorithme de hachage compte.
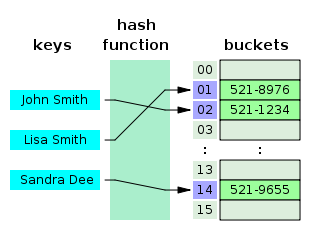
Bucket Table (sur wikipédia, CC-BY-SA)
Je ne vais pas m'étendre sur les HashTable, mais on peut déjà remarquer quelques problèmes dans les algorithmes qui permettent de les construire.
Le nombre possible de mots est immense. Par exemple, en ne prenant que les 26 lettres minuscules de l'alphabet latin, il existe $26^{10} = 1,411670957\times10^{14}$ mots de 10 lettres (comme "clementine"), si votre algorithme ne donne un résultat que sur 32 bits, il n'y a que $ 2^{32} = 4 \times 10^9$ digests différents. Cela met en évidence une chose : il peut y avoir deux mots qui ont le même hash. Pire, leur simplicité fait que ces doublons (appelés collision) sont prévisibles ! Cela signifie deux choses si je connais le hash je peux créer une fausse signature qui a le même hash. Ce qui n'est pas l'effet recherché.
C'est pourquoi on a créé des algorithmes de hashage dits cryptographiques. Ils utilisent des calculs plus complexes qui rendent leur falsification presque impossible.
Les plus connus sont md5 et sha1 (qui sont de moins en moins utilisés aujourd'hui pour les applications de sécurité). En effet, grâce à la puissance grandissante des ordinateurs et à la baisse des prix du stockage, des tables qui rassemblent un nombre important de digest avec les mots qui les ont générés ont été créées. De ce fait en les utilisant, on peut réussir à générer une collision2.
Aujourd'hui, on utilise les algorithmes de type sha2 qui rassemblent des algorithmes tels que sha256 et sha512. Ces Secured Hash Algorithms sont validés par la NSA et plusieurs grandes organisations qui travaillent sur la sécurité. Leur principe est open source et leur implémentation dans les langages habituels aussi. Vous pouvez par exemple trouver leur description sur wikipédia.
Afin de prévoir le jour où ces algorithmes seront aussi cassés, la famille sha3 qui se base sur le principe d'une fonction éponge a été créée.
-
Lorsqu'on crée des algorithmes qui manipulent des données on a tendance à les mettre dans des gros tableaux. Seulement pour trouver quelque chose dans un tableau, il faut le parcourir et si la donnée est à la fin, il faut parcourir toutes les cases. Avec une HashTable on trouve tout dans un temps qui ne dépend pas de la taille de la table. ↩
-
Sans compter que des faiblesses au sein même de l'algorithme ont été trouvées qui démontrent qu'un calcul distribué des collisions est efficace. ↩
Assurer l'intégrité du document et de l'acte
Si je vous ai parlé des algorithmes de hachage cryptographiques, c'est avant tout car ils ont des propriétés intéressantes dans le cas de la signature de document.
En effet, le mieux pour s'assurer qu'un document est intègre c'est-à-dire qu'il n'a pas été modifié, même très légèrement, c'est qu'au moindre petit changement dans le document, le changement dans la signature doit être important.
Notons aussi qu'il faut que les algorithmes demandent une certaine quantité de ressources afin de s'assurer qu'une attaque par force brute1 ne sera pas utilisée pour découvrir des collisions.
Ces algorithmes sont très connus des gestionnaires de paquets. Ces derniers créent un hash du fichier avant son envoi. Puis une fois l'envoi terminé, ils vous communiquent le hash. Il vous suffit alors de calculer le hash et de vérifier qu'ils sont identiques2.
Pour le cas de notre document que nous allons signer, il ne faut pas oublier la notion "d'acte" qui est inscrite dans le temps. C'est le 4 mai 2015 à 14h42 que j'ai envoyé mon document, pas hier, pas demain. Si je veux que mon document soit une preuve irréfutable, il faut donc que l'heure de la signature y soit intégrée. L'horodatage se fait souvent grâce au timestamp unix, c'est à dire le nombre de secondes depuis le premier janvier 1970.
-
Tester en masse des mots pour qu'ils donnent une collision. Cette technique peut se révéler viable grâce au paradoxe des anniversaires. ↩
-
Les antivirus utilisent aussi cette technique pour détecter un virus. Néanmoins, pour éviter la propriété qui fait changer le hash au moindre changement, ils utilisent un fuzzy hash algorithm (en) ↩
Tout en assurant l'authenticité.
Le principal but d'une signature, c'est de dire que c'est bien la personne qui a signé qui a envoyé le document. Pour cela, il va falloir s'inspirer de ce qu'il se fait en cryptographie.
Il serait trop long de faire un exposé des principaux algorithmes qui permettent la signature électronique. J'ai pris le parti de vous en présenter un qui se base sur un mot de passe connu de l'expéditeur et du destinataire.
Cet algorithme s'appelle HMAC pour Hash based Message Authentication Code. Il s'exprime par la formule :
En effet, comme l'acronyme nous l'indique, la fonction nommée H dans notre formule fait référence à un algorithme de hachage. On peut donc utiliser les outils déjà vus.
En pseudo-code, cela donnerait :
1 2 3 4 5 6 7 | message = "Mon épée est vôtre / Mon arc est vôtre / Et ma hache MAC." opad = 0x5c * X ipad = 0x36 * X mot_de_passe = string_vers_un_nombre_de_X_bits("Clem vaincra Cornichon") i_pad_mdp = mot_de_passe XOR ipad o_pad_mdp = mot_de_passe XOR opad hmac = sha1(o_pad_mdp + sha(i_pad_mdp + message)) |
Le HMAC n'est pas forcément l'algorithme le plus sécurisé à cause du fait que la "clé privée" doit être connue des deux participants. On préférera utiliser des algorithmes qui se basent sur RSA pour signer un document puis faire certifier par une autorité de confiance que la clef publique n'est pas atteinte.
Le HMAC est une solution très simple qui permet d'éviter ce surcoût tout en s'assurant que votre document est intègre. Et imaginer une situation dans laquelle la clef est connue de vous et de votre destinataire n'est pas si compliqué.
Imaginez un service qui vend des "signatures numériques dans le cloud". Son intérêt sera que vous ayez un compte chez lui, ainsi que votre destinataire. Il stocke alors des versions hachées de vos clefs privées à chacun et lorsque vous signez un document, lui il peut attester que vous êtes celui que vous prétendez être.
Notons enfin que dans la plupart des cas, HMAC possède une faiblesse : comme le mot de passe est connu des deux côtés, ZeZeste peut prétendre que ce n'est pas lui qui a signé le message mais Clem, on dit que HMAC est répudiable.
Dans le sens inverse, si Clem n'était pas une personne aussi sympa on pourrait penser que parfois elle signe des documents à la place des gens, on dit qu'elle leur impute ces documents. Il est bien évidemment souhaitable qu'une signature ne soit pas imputable.
Le mot de la fin
Si le concept de signature numérique, qui pourtant peut permettre d'améliorer votre confiance en les mails, factures, ou toute communication que vous recevez est en expansion, son utilisation n'est pas encore très connue du grand public. En effet, les outils à dispositions manquent soit de facilité d'accès (gpg/pgp par exemple) ou demandent un coût financier très élevé (certificat). Surtout, la défiance est d'autant plus forte que si le fait de signer un papier est quelque chose d'observable (ne prend-on pas en photo les mariés qui signent le registre d'état civil ?) la signature numérique se passe dans une boîte noire. Il faut donc en plus faire confiance aux logiciels et l'actualité nous a plus d'une fois montré les cas de failles volontaires ou non dans ces derniers.
Sources
- L'icône de cet article est publiée sous licence CC-BY-SA sur Wikipédia par Adobe Corporation sous le titre "Adobe EcoSign".
- L'algorithme spamsum qui permet de détecter la proximité entre deux messages différents (en).
- ANSSI (Agence Nationale de Sécurité des Systèmes d'Information.
- legifrance
- L'utilisation des algorithmes FNV et FNV1a (en).
- Utiliser gpg (fr).












