Début juillet 2022, s’est tenu le Congrès international des mathématiciens, au cours duquel, conformément à la tradition, la médaille Fields a été remise à de jeunes chercheurs ou chercheuses en mathématiques.

Le Congrès est le grand rendez-vous des mathématiciens ! Tous les quatre ans, il permet aux invités de se rencontrer, d’échanger et d’assister à des conférences par d’éminents chercheurs. Un moment fort de cet événement est la cérémonie de remise de la médaille Fields, qui récompense au plus quatre mathématiciens ou mathématiciennes de moins de 40 ans. Son prestige est tel qu’on la compare souvent au prix Nobel ! Cette année, le Congrès s’est tenu essentiellement à distance et non pas à Saint-Pétersbourg comme prévu initialement, pour cause de guerre russo-ukrainienne.
Cette année, les personnes lauréates sont, dans l’ordre alphabétique :
- le français Hugo Duminil-Copin de l’institut des hautes études scientifiques,
- l’américano-sud-coréen June Huh de l’université Stanford,
- le britannique James Maynard de l’université d’Oxford,
- l’ukrainienne Maryna Viazovska de l’école polytechnique fédérale de Lausanne.
Présentons cette mathématicienne et ces mathématiciens et surtout leurs travaux plus en détails !
- Hugo Duminil-Copin, spécialiste de la théorie des probabilités
- June Huh, spécialiste de géométrie algébrique et combinatoire
- James Maynard, spécialiste de théorie analytique des nombres
- Maryna Viazovska, spécialiste de géométrie
Hugo Duminil-Copin, spécialiste de la théorie des probabilités
Hugo Duminil-Copin est un jeune mathématicien français de 36 ans, qui s’intéresse particulièrement aux aspects mathématiques de la physique statistique. Autrement dit, il analyse rigoureusement des problèmes mathématiques émergeant de la physique statistique, une branche de la physique qui étudie le monde à travers le comportement aléatoire des particules, par exemple dans les gaz.

Physique statistique et changement de phase
Un des champs de la physique statistique est l’étude des changements de phase. Vous êtes sûrement familier des changements de phase de la vie courante, comme la glace qui se liquéfie pour se changer en eau, ou l’eau liquide qui bout pour se transformer en vapeur. La physique statistique s’intéresse à ce type de changement physique, qui ne concerne pas que des changements d’états, mais aussi d’autres phénomènes dans la matière tels que le ferromagnétisme.
Un des modèles mathématiques pour ces changements de phase est le modèle d’Ising, qui est un modèle très simplifié de la réalité physique, mais assez puissant pour expliquer partiellement certains phénomènes. Il consiste à considérer un quadrillage, où chaque intersection est occupée par un élément ayant un de deux états possibles. Pour le ferromagnétisme, un tel élément peut être un atome ayant pour état l’orientation de son champ magnétique, vers le haut ou vers le bas.
Une configuration du modèle s’obtient en tirant au sort les états des éléments. Ce tirage au sort ne se fait pas au hasard, mais en respectant des règles correspondant à des probabilités de répartition qu’on retrouve en physique, de sorte à prendre en compte des phénomènes par exemple lié à l’énergie d’une configuration, qui joue sur la taille des régions homogènes, ou à la température, qui augmente le désordre.
Un des comportements intéressant de ce modèle est la présence d’une transition de phase. Il existe une température particulière, à partir de laquelle le modèle change de comportement. D’un côté, le modèle est organisé avec une séparation assez claire en grandes régions homogènes, et à l’opposé, les régions restent petites et mélangées aléatoirement1. Le changement de comportement se produit rapidement à la température critique, laquelle a ainsi un comportement spécial et important, similaire aux choses intéressantes qui se passent lors d’un changement de phase en physique.
Le modèle d’Ising décrit ici présente également d’autres variantes qui forment toute une famille de modèles.
Les travaux récompensés
Hugo Duminil-Copin a obtenu sa médaille « pour avoir résolu de vieux problèmes en théorie probabiliste des transitions de phases en physique statistique, plus spécifiquement en dimensions trois et quatre2 ».
Hugo Duminil-Copin a contribué à de nombreux résultats sur des modèles voisins du modèle d’Ising, notamment en prouvant des résultats d’invariances par certaines symétries au point critique, qui renseignent sur le comportement de ces modèles. Il a aussi produit des résultats sur la continuité et la discontinuité de la transition de phase pour certaines classes de modèles. Les dimensions trois et quatre sont spécifiquement citées car elles présentent certaines difficultés qu’on ne retrouve pas en dimension deux ni en dimensions supérieures.
Ces travaux font avancer la compréhension du domaine et sont un jalon vers des questions plus complexes et profondes, qui ne seront pas abordées ici.
- Voir ce document, Figure 1, p. 3 pour une illlustration du modèle.↩
- En version originale : « for solving longstanding problems in the probabilistic theory of phase transitions in statistical physics, especially in dimensions three and four ».↩
June Huh, spécialiste de géométrie algébrique et combinatoire
June Huh est un mathématicien américano-sud-coréen né en 1983, qui travaille à la frontière entre la géométrie algébrique et la combinatoire. Autrement dit, il se place à l’interface entre l’étude des formes à travers des équations (la géométrie algébrique) et le dénombrement d’objets comme discipline mathématique (la combinatoire).

Géométrie et dénombrement
Un des problèmes les plus basiques de la géométrie combinatoire est le décompte de droites étant donné un ensemble de points du plan. Deux points suffisent à définir une droite, mais en fonction de la configuration, certaines peuvent être confondues. Il ne suffit donc pas de compter le nombre de paires de points ! La figure ci-dessous illustre ce point.
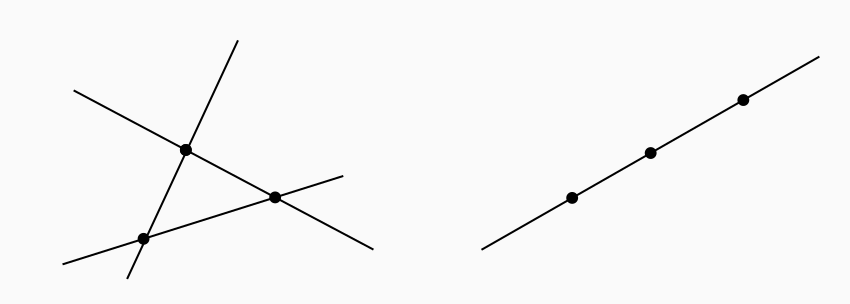
Dans l’espace à trois dimensions usuel, on peut compter des droites (définies par deux points) et des plans (définis par trois points). Ces questions de dénombrement se généralisent encore plus : dans des espaces à d dimensions, ou aussi en comptant autre chose que des droites (des hyperplans par exemple), et bien sûr en changeant le nombre de points, et en explorant les configurations spéciales.
Pour aller plus loin, la situation présentée ci-avant peut se transposer aux matroïdes, des structures plus abstraites qui généralisent les notions d’incidence (le fait qu’une droite est définie par deux points, un plan par trois points, etc.) en des notions plus générales, tout en conservant le cœur de l’idée. Ce sont des abstractions combinatoires de configurations géométriques. On retrouve des matroïdes dans les espaces projectifs, les extensions de corps et bien d’autres domaines.
Comme le montre la figure ci-dessus, les différentes configurations possibles, surtout celles particulières, peuvent être très nombreuses. Il y a en particulier plus de configurations spéciales dans les plus grandes dimensions et elles varient en fonction de l’objet exact qu’on considère (différent types de matroïdes par exemple). Cela n’empêche pas de vouloir démontrer des propriétés de dénombrement.
Un ensemble de questions portent sur l’évolution du nombre de droites, plans, etc. (ou leurs analogues) à mesure que le nombre de points nécessaires pour les définir augmente (plus rigoureusement le rang). Plus spécifiquement, les mathématiciens se questionnent sur l’unimodalité (est-ce que la suite présente une unique bosse ?) et la comparaison du dénombrement pour différents rangs (y a-t-il plus de plans que de droites pour une configuration de points donnée ?).
Les travaux récompensés
June Huh a obtenu sa médaille « pour l’apport à la combinatoire des idées de la théorie de Hodge, la démonstration de la conjecture de Dowling-Wilson pour les treillis géométriques, la démonstration de la conjecture de Heron-Rota-Welsh pour les matroïdes, le développement de la théorie des polynômes lorentziens et la démonstration de la conjecture forte de Mason1 ».
La conjecture (désormais théorème) de Dowling-Wilson pour les treillis géométriques est un résultat décrivant l’évolution du nombre d’objets en fonction du rang pour une configuration donnée ; June Huh a pu la prouver pour les treillis géométriques, un type particulier de matroïdes.
Les autres théorèmes relient étroitement les matroïdes à une classe particulière de polynômes, les polynômes lorentziens. June Huh a contribué à développer leur théorie, prouvé un résultat important à leur sujet en introduisant des idées nouvelles dans la combinatoire (les théories de Hodge). La conjecture de Mason forte a également trait à ce domaine.
- En version originale : « for bringing the ideas of Hodge theory to combinatorics, the proof of the Dowling–Wilson conjecture for geometric lattices, the proof of the Heron–Rota–Welsh conjecture for matroids, the development of the theory of Lorentzian polynomials, and the proof of the strong Mason conjecture ».↩
James Maynard, spécialiste de théorie analytique des nombres
James Maynard est un mathématicien britannique de 35 ans, professeur à l’université d’Oxford. Il travaille en théorie analytique des nombres, la branche des mathématiques qui utilise les outils de l’analyse (les fonctions, dérivées, intégrales, etc.) pour étudier les entiers. Il étudie en particulier les écarts entre nombres premiers, objets phares de la théorie des nombres.

La structure des nombres premiers
Les nombres premiers sont des objets mathématiques simples à définir : ce sont les entiers naturels qui ont exactement deux diviseurs : 1 et eux-mêmes. Par exemple, 5 est premier, il n’est divisible que par 1 et 5. L’entier 6 n’est pas premier, il est divisible par 2 et 3 en plus de 1 et 6.
Les nombres premiers sont en nombre infini. En effet, si l’on suppose qu’ils existent en nombre fini , qu’on nomme à , alors on peut fabriquer le nombre qui est premier mais n’est pas dans la liste précédente, il s’agit d’une contradiction, et on peut faire cela pour tous les entiers, et on en déduit qu’il y a une infinité de nombres premiers.
Une question qui se pose à partir de là, est celui de leur répartition globale. Y en a-t-il de moins en moins à mesure qu’on avance vers l’infini ? Peut-on estimer grossièrement leur proportion ? La réponse à ces deux questions est oui. La réponse est donnée par le théorème des nombres premiers, qui dit que le compte de nombres premiers inférieurs ou égal à un réel donné évolue de manière similaire à pour les très grands. Autrement dit, les nombres premiers se raréfient à mesure qu’on avance vers l’infini, et on a une mesure de la vitesse de décroissance. Ce théorème a été démontré avec des outils de l’analyse, et a marqué la naissance de la théorie analytique des nombres. Ce que l’on suppose être une encore meilleure estimation est liée à la conjecture de Riemann, mais la démonstration de cette conjecture, si elle est vraie, paraît inaccessible pour le moment.
On peut aussi s’intéresser à la répartition locale des nombres premiers, notamment via l’écart entre premiers consécutifs. Une conjecture importante, mais toujours non démontrée, est celle des nombres premiers jumeaux, qui stipule qu’il existe une infinité de paires de nombres premiers consécutifs dont la différence vaut 2. De nombreuses avancées majeures ont été faites récemment (voir ces slides de Terence Tao datant déjà de 2015), qui démontrent qu’il y a une infinité de nombres premiers consécutifs écartés d’au plus 246 (voire moins, si j’ai raté les tous derniers développements). Se pose aussi la question de la manière dont l’écart maximal entre nombres premiers consécutifs augmente à mesure que les nombres premiers grandissent. Ces problèmes ont également des variantes, où on regarde l’écart non pas entre premiers consécutifs, mais entre premiers séparés par un ou plusieurs autres nombres premiers.
Les travaux récompensés
James Maynard a obtenu sa médaille « pour des contributions à la théorie analytique des nombres, qui ont mené à des avancées majeures dans la compréhension de la structure des nombres premiers et de l’approximation diophantienne1 ».
James Maynard a fourni des idées nouvelles, autour des techniques de crible, et des résultats surprenants au sujet de la répartition des nombres premiers, qui ont permis de descendre l’écart évoqué précédemment à 600 alors que les techniques précédentes ne permettaient plus d’avancées. Ce record a ensuite été amélioré à 246 par un effort collectif. Ces idées ont aussi permis de prouver la présence d’une infinité de groupes de 2, 3, 4, etc. nombres premiers pas trop éloignés les uns des autres. À l’opposé, il a aussi pu prouver la présence de zones moins denses en nombres premiers que la moyenne, cette question ayant peu progressé depuis des décennies.
L’autre travail mentionné concerne l’approximation diophantienne, c’est-à-dire l’approximation des réels par des rationnels. J’ai choisi de ne pas développer le sujet dans le présent article, car moins abordable, mais il reste intéressant, et toujours en théorie des nombres !
- En version originale : « for contributions to analytic number theory, which have led to major advances in the understanding of the structure of prime numbers and in Diophantine approximation ».↩
Maryna Viazovska, spécialiste de géométrie
Maryna Viazovska est une mathématicienne ukrainienne né en 1984. Elle étudie la géométrie, et plus particulièrement le problème de l’empilement compact de sphères. De formulation simple, les différentes variantes de ce problème de géométrie donnent du fil à retordre aux mathématiciens.

Empilement compact de sphères
L’empilement compact de sphère est un problème surprenamment simple à formuler et pourtant terriblement dur à traiter.
En deux dimensions, il s’agit d’empiler des cercles (ce sont des sphères à deux dimensions). L’empilement le plus compact est un empilement où chaque cercle a 6 voisins organisés dans un réseau hexagonal régulier. La preuve que ce réseau est le plus optimal des réseaux a été faite par Gauss, mais il a fallu attendre 1940 et le travail de Fejes Tóth pour prouver que c’était le meilleur de tous les empilements possibles, en incluant également ceux qui ne sont pas des réseaux !
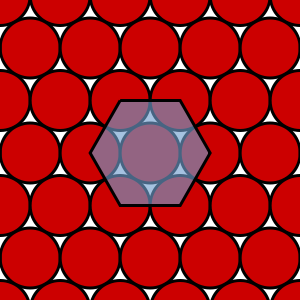
En trois dimensions, le travail mathématique a également été compliqué. L’empilement sous forme de réseau régulier qu’on connait tous, s’appelle D3. Il a été montré comme optimal parmi les empilements sous forme de réseaux par Gauss en 1831, mais la preuve qu’il s’agit du meilleur empilement de tous les empilements, et pas seulement sous forme de réseau, a été faite après des calculs informatiques d’optimisation assez lourds par Thomas Callister Hales en 1998 ; l’article a même mis plusieurs années à être revu par la communauté avant publication !

Que se passe-t-il pour les dimensions plus grandes ? D4 et D5, des analogues de D3 à plus grande dimension, sont les réseaux les plus compacts, mais sans qu’il soit démontré qu’il s’agisse des empilements les plus compacts en incluant également ceux qui ne sont pas des réseaux réguliers. En plus grande dimension encore, des cas particuliers apparaissent. E8, l’empilement désormais prouvé le plus compact à 8 dimensions, est un de ces cas, tout comme Λ24 !
Entre les cas particuliers décrits ci-avant, les dimensions intermédiaires recèlent encore une part de mystère, et font de cet empilement de sphères un problème plus intéressant qu’il n’y paraît à première vue.
Les travaux récompensés
Maryna Viazovska a obtenu sa médaille « pour la démonstration du fait que le réseau E8 fournit l’empilement le plus compact de sphères en 8 dimensions, et d’autres contributions à des problèmes extrémaux connexes et à des problèmes d’interpolation en analyse de Fourier1 ».
Cette preuve se base sur la construction d’une fonction « magique ». Cette fonction est périodique, en lien avec la périodicité du réseau E8 et il s’agit d’une solution d’un problème extrémal, car cette fonction atteint une borne générale déjà identifiée auparavant pour la compacité, ce qui la rend maximale et prouve qu’E8 est bien l’empilement le plus compact possible. L’analyse de Fourier apparaît naturellement dans ce type de problèmes où l’on travaille sur des réseaux périodiques.
- En version originale : « for the proof that the E8 lattice provides the densest packing of identical spheres in 8 dimensions, and further contributions to related extremal problems and interpolation problems in Fourier analysis ».↩
Références
- La page des médailles Fields 2022 sur le site de l'IMU.
- Portrait de June Huh sur la chaîne Youtube de l'ICM.
- Portrait de Hugo Duminil-Copin sur la chaîne Youtube de l'ICM.
- Portrait de Maryna Viazovska sur la chaîne Youtube de l'ICM.
- Portrait de James Maynard sur la chaîne Youtube de l'ICM.


