Générer de la musique grâce aux chaînes de Markov
Ce billet est publié en parallèle sur le blog de RTFMCorp..
Il y a quelques temps maintenant, sur le forum de ce même site, j’ai créé un sujet pour parler d’un projet sur lequel je travaillais dans le cadre de mon travail de Bachelor à l’Université de Fribourg.
Le projet consistait à créer un programme capable de générer des mélodies de musique irlandaise après avoir analysé une banque de données de morceaux originaux et en avoir tiré certaines statistiques intéressantes sur la façon dont les morceaux sont écrits.
Plusieurs personnes semblaient plutôt intéressées d’en savoir un peu plus sur le projet, comme je n’ai ni la prétention d’écrire un tuto ni le temps de faire un article complet, je profite des tribunes libres pour partager les quelques unes des connaissances que j’ai pu acquérir pendant cette expérience.
Les chaînes de Markov
En bref, une chaîne de Markov (si vous n’avez pas peur de quelques maths, l’article de wikipedia est assez complet) est un graphe d’état dirigé pondéré, dont le poids des arrêtes représente la probabilité d’aller vers l’état connecté (en vrai c’est un peu plus que ça, mais c’est cette notion qui va nous intéresser.). Le but d’une chaîne de Markov est d’établir la probabilité des états futurs d’un système en connaissant l’état présent.
Reprenons depuis le début
Un Graphe ?
Un graphe est un ensemble de sommets (que l’on appellera plus tard "états") et d’arêtes (que l’on appellera plus tard "arêtes"), chaque arête relie deux sommets entre eux.
Pour les férus de formalisation mathématique ça se note comme ça : $G = (V,E)$ avec $E = \{\{i,j\} \in V^2\}$
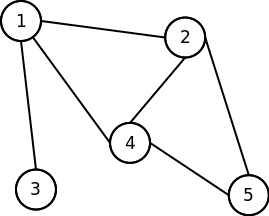
Donc comme on le voit sur l’image ci-dessus il s’agit simplement de plusieurs sommets reliés entre eux par des arêtes; deux sommets ne peuvent être reliés entre eux qu’une fois et un sommet peu être relié à lui-même (ici les chiffres servent simplement de numérotation pour identifier les différents sommets). Les arêtes sont à voir comme des ponts, ici par exemple, depuis le sommet n°1 on peut rejoindre les sommets n°2, 3 et 4.
Un Graphe d’états ?
Rien de bien compliqué ici, il s’agit d’une dénomination purement symbolique. Le but des chaînes de Markov étant d’anticiper les états futurs possibles d’un système, les sommets d’un graphe servent donc à symboliser ces états. C’est pourquoi nous parlerons désormais d’états à la place de sommets.
Un Graphe d’états dirigé ?
Apportons une petite modification à notre graphe. Avant, les arêtes faisaient office de pont entre deux états; et si nous mettions des ponts à sens unique ? Le terme "dirigé" prend alors tout son sens, non ?
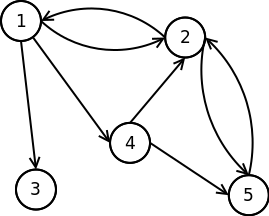
Comme on le voit ci-dessus, chaque arête est maintenant représentée par une flèche, qui symbolise le sens dans lequel on peut se déplacer. Dans cet exemple, depuis l’état n°1, on peut toujours rejoindre les états n°2, 3 et 4, mais depuis l’état n°3 par exemple, on reste bloqué. On voit maintenant que deux états peuvent être reliés entre eux deux fois, une fois pour un sens, une autre fois pour l’autre.
Un Graphe d’états dirigé pondéré ?
Et oui ! A présent, on va rajouter des valeurs à nos ponts. Je le rappelle, le but à la base est de pouvoir établir des probabilités sur les états futurs possibles d’un système donné. On va donc ajouter sur chaque pont un nombre indiquant la probabilité que celui-ci soit emprunté.
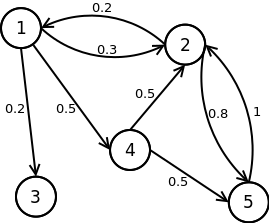
Et voilà un exemple de chaîne de Markov ! Ici, nous avons attribué à chaque arête un poids (d’où le terme "pondéré") représentant la probabilité qu’à partir d’un état donné, on rejoigne l’état relié par cette arête. Comme il s’agit d’une probabilité, chaque poids se situe entre 0 et 1, le 0 étant noté par l’absence d’arête et représentant une probabilité nulle, le 1 représentant une probabilité absolue. De plus, la somme des poids de chaque arête partant du même état doit être égale à 1.
Dans cet exemple, depuis l’état n°4 nous avons 1 chance sur 2 d’atteindre l’état n°2 et 1 chance sur 2 d’atteindre l’état n°5.
Et la musique alors ?
On y vient ! Maintenant que nous savons ce qu’est une chaîne de Markov, nous pouvons l’utiliser pour définir des règles sur la manière dont nos mélodies seront écrites. Pour une partition donnée, nous allons établir un programme qui pointera sur une note, l’état courant de notre système correspondra alors à la note en question. Nous pourrons alors établir des probabilités sur la note suivante.
Admettons que nous sommes en train d’écrire une mélodie et que nous avons déjà écrit les notes suivantes :
Pour composer la suite de notre mélodie, nous allons simplement regarder la dernière note écrite, celle sur laquelle pointe notre programme (ici la note marquée en rouge, un Do). Nous allons alors regarder notre chaîne de Markov :
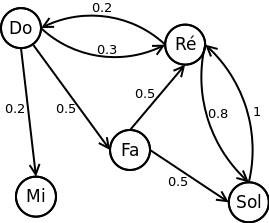
Etant donnée la dernière note (un Do), nous sommes donc sur l’état "Do". Selon les règles établies par la chaîne de Markov ci-dessus, la note suivante a alors 20% de chance d’être un Mi, 50% de chance d’être un Fa et 30% de chance d’être un Ré.
Et c’est tout ?
Et bien oui, c’est la base de l’idée.
Mais c’est nul, on choisit donc la note suivante à partir de la dernière note uniquement ?
Effectivement, pour rappel, une chaîne de Markov sert à prévoir l’état futur avec pour seule donnée l’état présent ! Mais on peut tout de même améliorer le système en "trichant" un peu. On va essayer de simuler une "mémoire" en augmentant le nombre d’états. En fait, c’est assez simple. Au lieu de prendre en compte seulement la dernière note, on va prendre en compte les deux dernières, ou les trois dernières etc…
Essayons de prendre en compte les deux dernières notes. Pour faire cela, chaque état ne représentera plus une seule note mais plutôt un groupe de notes (en l’occurrence un couple). Ainsi, pour reprendre l’exemple précédent, au lieu de partir d’un état "Do", étant donné que l’avant-dernière note est un Ré, nous allons partir d’un état "Ré-Do". Tous les états vers lesquels nous pourrons alors nous diriger seront des états montrant que l’avant dernière note était, avant d’en écrire une nouvelle, un Do.
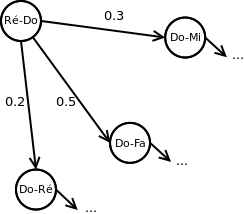
Dans cet exemple, seulement la partie de la chaîne qui nous intéresse apparaît, la partie centrée sur l’état "Ré-Do". Nous voyons que selon les règles de cette chaîne de Markov, après les notes Ré et Do nous avons 20% de chance de voir un Ré, 50% de chance de voir un Fa et 30% de chance de voir un Mi.
Comme nous prenons en compte les deux dernières notes de la mélodie, nous allons alors parler d’une chaîne de Markov de degré 2. Nous pouvons augmenter le degré de notre chaîne de Markov autant qu’on le souhaite.
Quelques contraintes pratiques…
Autant qu’on le souhaite ? En théorie peut-être mais dans la pratique, au bout d’un moment ça commence à faire beaucoup, mais alors beaucoup d’états. Prenons notre toute première méthode : la chaîne de Markov de degré 1, celle qui prend en compte uniquement la dernière note. Nous aurons en toute logique un maximum de 12 états, 12 étant le nombre de notes qui existent dans la gamme (en prenant en compte la gamme traditionnelle occidentale et en excluant les octaves bien sûr 
).
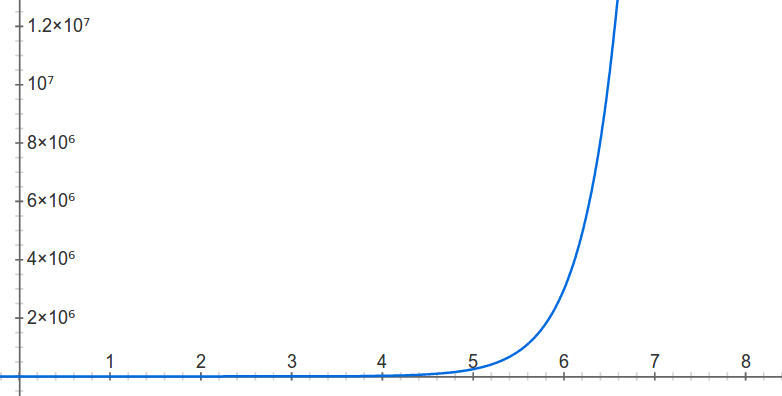
Essayons maintenant de construire une chaîne de degré 2, le maximum d’état sera donc de $12^2 = 144$; comme il y a 12 notes dans la gamme et que nous prenons en compte des couples de notes, nous avons bien $12 \cdot 12$ états possibles. Vous le voyez venir ? Et oui, la quantité d’états croit exponentiellement. Soit $n$ le nombre de notes à prendre en compte pour générer la note suivante et $|V|$ le nombre d’états, on a $|V| = 12^n$, ce qui nous donne ceci :
Voilà, nous avons fait le tour de la théorie à la base de mon projet de génération de mélodies de musique irlandaise. Bien évidemment, tout le projet ne se résume pas uniquement à ça. Donc pour ceux qui veulent en savoir plus et n’ont pas peur de l’anglais, vous pouvez télécharger mon rapport complet (incluant notamment les résultats des tests) ici.
Allez, salut à tous !
C’est intéressant de voir qu’avec une méthode de génération relativement simple, et sans avoir besoin d’encoder dans un algorithme des règles de composition, on arrive à des résultats concluants.
