Ah ce sujet est vraiment intéressant. Aux premiers instant on aperçois le schéma d’une brasserie. Rien de plus réjouissant pour commencer son examen. J’aurais aimé avoir le même sujet ! 
Voici ma proposition de résolution, elle s’appuie notamment sur la proposition incomplète offerte par Studyrama.
- Partie 1 - Dosage conductimétrique des ions chlorure dans une eau de brassage
- Partie 2 - Autour de la fermentation
- Partie 3 - Le conditionnement de la bière
Partie 1 - Dosage conductimétrique des ions chlorure dans une eau de brassage
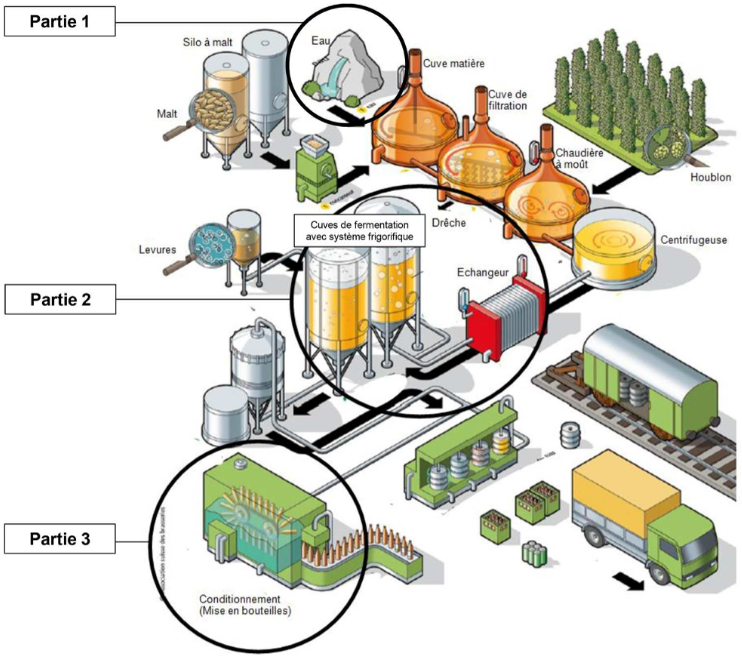
1.1 À l’aide de la figure 1 page $2$, citer les matières premières utilisées dans la fabrication de la bière.
Nous avons typiquement une question de lecture de document. Les entrées, c’est ça qu’il faut regarder :
- Eau
- Levures
- Houblon
- Malt
Vous ne pouviez pas le deviner mais il s’agit surement du Malt d’orge typique (une graine germée). Il suffisait de suivre les flèches directionnelles qui nous indiquées d’où venait les matières premières pour résoudre cette question.
Énoncé : En brasserie, les bières sont toutes produites selon le même procédé. Cependant, en fonction notamment de l’eau utilisée pour le brassage, toutes ne possèdent pas les mêmes caractéristiques (goût, aspect, etc…). Afin de savoir si l’eau utilisée pour le brassage convient pour une production de bière brune, il faut doser les ions chlorure. Pour ce faire, on procède à un titrage par une solution de nitrate d’argent $\mathrm{(Ag^+_{(aq)} + NO^-_{3(aq)})}$. Le dosage est suivi par conductimétrie. L’équation de la réaction de dosage est la suivante :

1.2 En s’aidant des valeurs de conductivités ioniques molaires données dans le document 1 page $7$, justifier l’allure de la courbe de dosage fournie dans le document réponse en annexe page $9$. Montrer ensuite graphiquement sur le document réponse que le volume équivalent $V_e$ vaut $12,0$ mL.

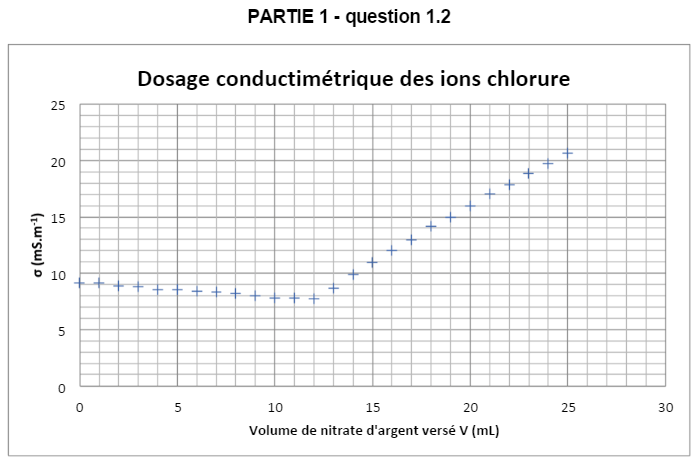
Au départ on peut avoir peur et se dire qu’on aura besoin de la loi de Kohlrausch qui est clairement au cœur du chapitre de l’analyse conductimètre du cycle de terminale STL-SPCL.
Mais pas du tout, donc ne nous compliquons pas la tâche pour rien et allons au plus simple :
Alors ici je vais séparer en deux idées :
- L’équivalence se lie facilement
- Explications partie par partie des zones de la courbe à l’aide des coefficients de conductivité molaire donné dans le tableau
Le premier point est simple, on vous dit que l’équivalence est à $12.0$ mL, et en plus vous voyez vous même que la courbe change de forme lorsqu’elle passe au dessus du $12$ de l’axe des abscisses. C’est la question : "Qui sait lire le graphique ?" du coups vous imaginez bien qu’elle n’est pas l’essence même de la question… Donc si vous voulez les points il va falloir étayer :
Le volume équivalent se trouve en traçant les droites des deux zones respectives de la courbe. L’intersection de ces deux droites nous donnera un point situé au volume équivalent sur l’axe des abscisses :
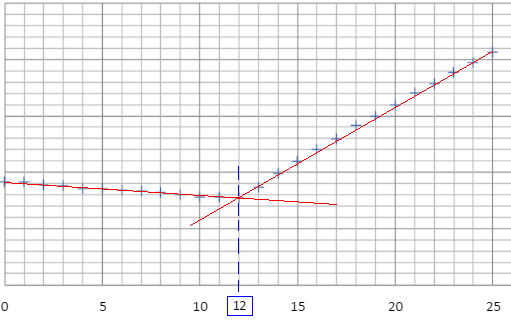
Avant l’équivalence nous avons donc une zone ou la conductivité baisse un tout petit peu. Rien de bien impressionnant. Pourquoi ?

Et bien la raison est clairement liée à la manipulation. Que faisons nous ? Nous ajoutons à l’eau de brassage, qui contient des chlorures, des ions $\mathrm{Ag^+}$. Les ions chlorures précipitent sous forme de $\mathrm{AgCl_{(s)}}$. Donc ils quittent la solution, ne sont plus ionique, donc ne conduisent plus l’électricité.
- Les ions chlorures sont responsables de $\sigma = 9\;mS.m^{-1}$
- Puis on ajoute des $\mathrm{Ag^+}$ qui vont éliminer les $\mathrm{Cl}^-$
- Substentiellement on ajoute des $\mathrm{NO_3^-}$ qui ont une conductivité moins élevé que les chlorures
- On aura finalement substitué l’anion $\mathrm{Cl^-}$ par des $\mathrm{NO_3^-}$ moins conducteur, normal que la conductivité baisse
Après que l’équivalence soit atteinte on a plus de chlorure qui puissent réagir avec l’argent. Donc ce qui se passe typiquement :
- On ajoute des ions $\mathrm{Ag}^+$ à une solution inerte (qui ne réagit plus)
- La quantité de $\mathrm{NO_3^-}$ continue elle aussi à grimper
- La concentration en ion augmente sans s’arrêter d’où l’augmentation de la conductivité de la solution $\sigma = 21\;mS.m^{-1}$
1.3 Calcul de la concentration massique en ions chlorure.
- Déterminer la valeur de la concentration molaire en ions chlorure $\mathrm{C_{Cl^-}}$ de l’eau de brassage
- La masse molaire atomique du chlore vaut $\mathrm{M = 35,5\;g.mol^{-1}}$ . Montrer que la concentration massique en ions chlorure $C_M = 42.6\;mg\cdot L^{-1}$.
Avec :
- $\mathrm{C_{Ag^+} = 10\;mmol \cdot L^{-1}}$
- $\mathrm{V_e = 12.0\;mL = 0.012\;L}$
- $\mathrm{V_1 = 100\;mL = 0.1\;L}$
Nous avons de quoi déterminer la concentration molaire d’ions chlorures :
Maintenant pour convertir en concentration massique (en faisant attention aux unités !) on utilise $\mathrm{C_n \cdot M= C_{massique}}$.
1.4 On cherche à estimer l’incertitude sur la concentration massique en ions chlorure $\mathrm{U_{(C_M)}}$ dans l’eau de brassage.
- L’incertitude $\mathrm{U_{(V_1)}}$ sur le volume de l’eau de brassage $\mathrm{V_1}$ est de $\mathrm{1\;mL}$. On estime que l’incertitude $\mathrm{U_{(Ve)}}$ sur la détermination du volume équivalent $\mathrm{V_e}$ vaut $\mathrm{0,5\;mL}$. On admet que la relation de propagation des incertitudes s’écrit :
Comparer l’influence des différentes sources d’erreur sur l’estimation de U(C)et M justifier qu’une d’entre elles est prépondérante devant les autres.
- En ne tenant compte que de la source d’erreur prépondérante, calculer $\mathrm{U_{(C_M)}}$ puis écrire correctement la concentration massique en ions chlorure de l’eau de brassage $\mathrm{C_M}$ avec son incertitude.
C’est pas la partie qui m’intéresse le plus ce n’est pas mon fort… Donc j’vous laisser avec la correction de studyrama page $2$ et $3$ ici.
1.5 D’après le document 2, déterminer si cette eau convient pour la fabrication d’une bière brune.

Encore une fois petite séance de lecture de document. On a, pour rappel, $\mathrm{C_{Cl^-} = 42.6\;mg\cdot L^{-1}}$. Nous avons donc une bière avec une eau limpide et une dureté en bouche faible puisque ne sommes largement sous la barre des $\mathrm{70\;ppm}$. Nous avons là une bière légère, très certainement une bonne blonde !
Partie 2 - Autour de la fermentation
Énoncé : La fermentation du moût est un processus exothermique. Elle nécessite une température optimale de $\mathrm{9,0°C}$, or le moût sort de la dernière cuve de brassage à $\mathrm{100,0°C}$. Pour assurer une bonne fermentation, il est donc nécessaire de :
- refroidir le moût de $\mathrm{100,0°C}$ à $\mathrm{9,0°C}$ . La rapidité du refroidissement est cruciale afin à d’éviter l’infection par d’éventuelles bactéries. On utilise pour cela un échangeur à plaques.
- durant toute la fermentation à l’aide d’un système maintenir le contenu de la cuve à $\mathrm{9,0°C}$ frigorifique.
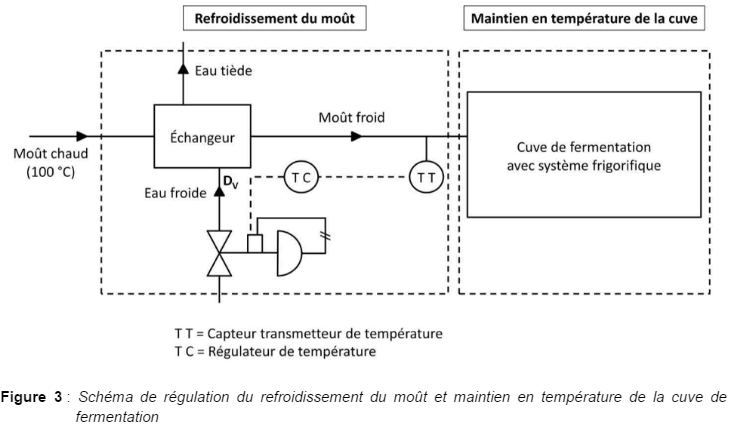
A - Le refroidissement du moût.
Énoncé : L’échangeur est alimenté par de l’eau froide ; il en ressort de l’eau tiède qui pourra être réutilisée dans une autre partie de l’usine. Le débit volumique d’eau froide $\mathrm{D_V}$ peut être modifié avec une vanne commandée par un régulateur, en lien avec le capteur de température placé à la sortie de l’échangeur.
2.1 L’eau et le moût circulent à contre-courant dans l’échangeur. Justifier ce choix.
Faire circuler à contre courant qu’est ce que ça veut dire et à quoi ça sert ? C’est réellement ça qui est demandé dans cette question.
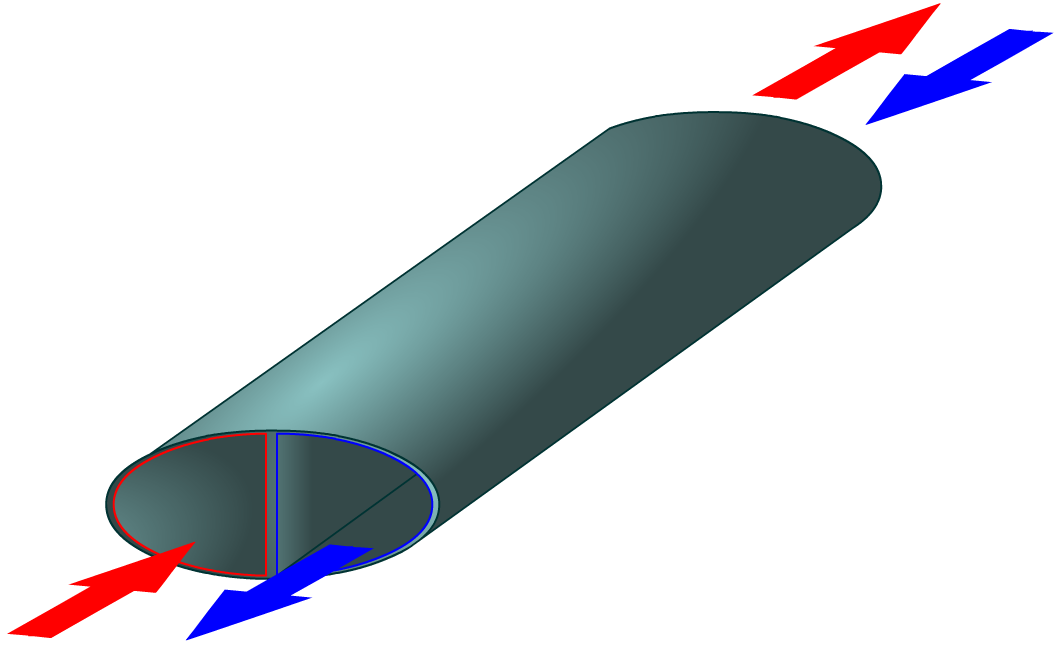
Le fluide chaud (rouge) arrive par un coté où le fluide froid (bleu) lui en sort. C’est ça un contre courant. Mais en quoi c’est un choix judicieux ?
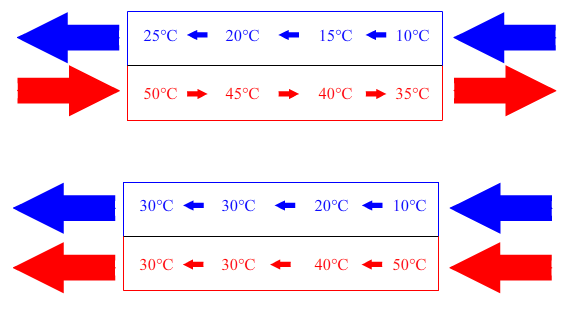
Le premier est le schéma (avec le gradient de température) de deux fluide à contre-courant. On voit qu’à la fin (à chaque sortie ou entrée) les températures ne sont pas égales, on peut échanger de la chaleur.
Dans le deuxième cas, cas co-courant le fluide très chaud arrive proche du très froid et échange beaucoup de chaleur. A la fin les deux fluides sont à la température d’équilibre et n’échange plus rien.
A l’aide de ce genre de comparaison vous pourrez montrer que :
- vous avez compris qu’il s’agit d’un système différent et meilleur que le système co-courant
- vous avez pu éviter de vous faire prendre au piège avec une explication bancale
Ne pas improviser des définitions si vous avez des problèmes de clarté, si vous avez un schéma en tête, dessinez le.
2.2 Le fonctionnement de l’échangeur est régi par un régulateur. Indiquer la grandeur réglée, la grandeur réglante et la valeur de la consigne
Nous venons de passer 5 minutes à réfléchir à la température dans un système, nous sommes tenté de répondre :
- "Bah on va régler la température non ?"
Mais c’est une question qui se positionne comme un petit piège. Car en réalité on ne va pas s’amuser à chauffer ou refroidir certains liquide. Ici on va surtout s’assurer du débit d’eau froide qui lui réglera finalement la température.
C’est bien plus coûteux en énergie de refroidir (perte par dissipation thermique, achat de materiel) de l’eau froide qui circule dans un tuyaux. Alors que nous avons a disposition de toute façon :
- Une pompe qui achemine l’eau
On est obligé d’avoir quelque chose qui envoie de l’eau dans les tuyau autant simplement régler cet appareil pour simplement mettre $2$ fois plus d’eau dans les tuyaux.
- Grandeur réglée : Température actuelle
- Grandeur réglante : Le débit d’eau froide
- Valeur de la consigne : Température finale qui nous satisfasse
B - Maintien en température de la cuve de fermentation
Énoncé : Durant toute la fermentation (une semaine), la température intérieure de la cuve doit être maintenue à $\mathrm{9,0°C}$. Pour ce faire, un système frigorifique est installé sur la cuve de fermentation. Ce système permet par ailleurs de réchauffer de l’eau stockée dans un bassin. Cette eau sera ultérieurement utilisée comme eau de brassage (document 3). La température de la pièce dans laquelle se trouve la cuve est de $\mathrm{21°C}$.
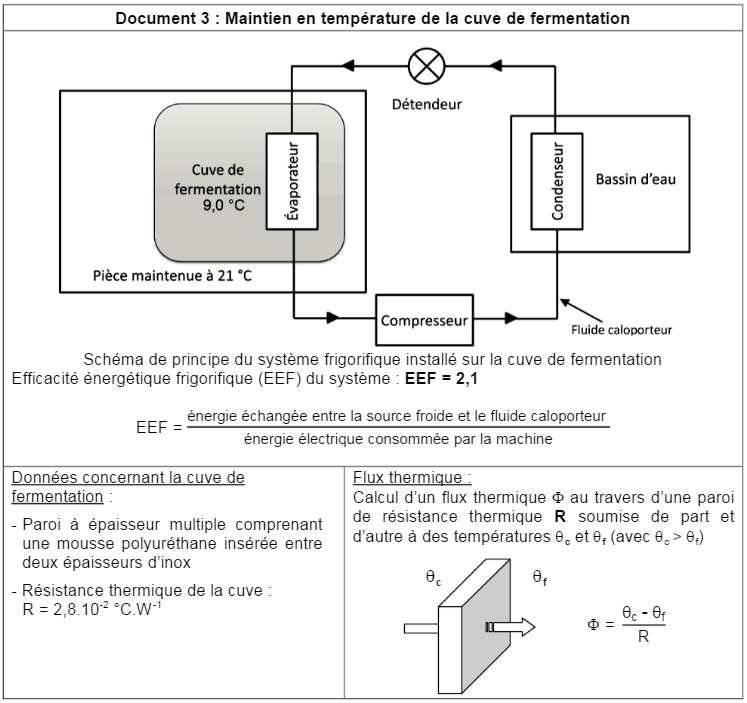
2.3. Nécessité d’un système de refroidissement :
-
À l’aide du document 3, montrer que le flux thermique $\Phi$ la paroi de la traversant cuve est de l’ordre de $\mathrm{430\;W}$.
-
En vous appuyant sur vos connaissances et en le justifiant, préciser le sens du transfert thermique à travers la paroi de la cuve. Justifier la nécessité d’un système de refroidissement.
Là on essaye de vous aider au maximum avec un document 3 qui vous donne la formule d’obtention de $\Phi$ :
L’ordre de $\mathrm{430\;W}$ est clairement respectés.
Maintenant le sens de transfert il faut bien comprendre que ce dont on parle quand on parle de chaleur c’est d’agitation microscopique. Plus la température est élevé plus les molécules sont agités, c’est ça la notion de température. La chaleur est la transmission de cette agitation : un peu comme si nous étions dans une foule si tout le monde se remue de droite un gauche on est un peu forcer de faire pareil. Quand on a un liquide chaud (très agité à l’échelle microscopique) face à un liquide froid, c’est l’agitation qui va être contagieuse.
Par exemple la phrase "Ferme la fenêtre tu vas faire rentrer le froid" n’a pas de sens, puisque c’est la chaleur qui se diffuse et se partage.

Tout ça pour dire : les transfert s’effectue de la source la plus chaude vers la source la plus froide.
Pour l’histoire de la fermentation nous avons besoin de refroidir le moût à $\mathrm{9,0°C}$ car il est à une température trop élevé pour que la fermentation se déroule selon le protocole de la conception de la bière qui est mis en jeu.
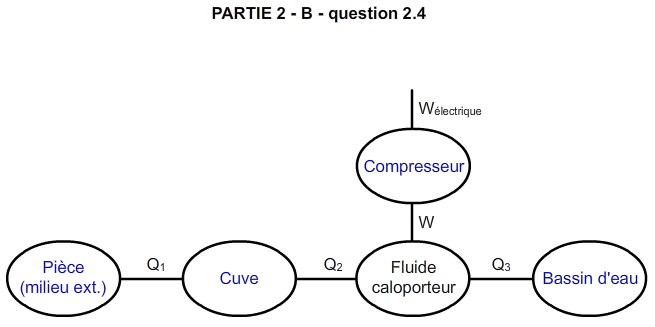
2.4 Sur le document réponse en annexe page 9, à rendre avec la copie, compléter le schéma énergétique du système en sélectionnant certaines expressions parmi celles proposées dans la liste suivante :
- Bassin d’eau
- Compresseur
- Cuve de fermentation
- Détendeur
- Pièce
- Fluide caloporteur.
Préciser à l’aide de flèches le sens réel des transferts énergétiques notés $\mathrm{Q}$ pour des transferts thermiques, et $\mathrm{W}$ pour du travail.
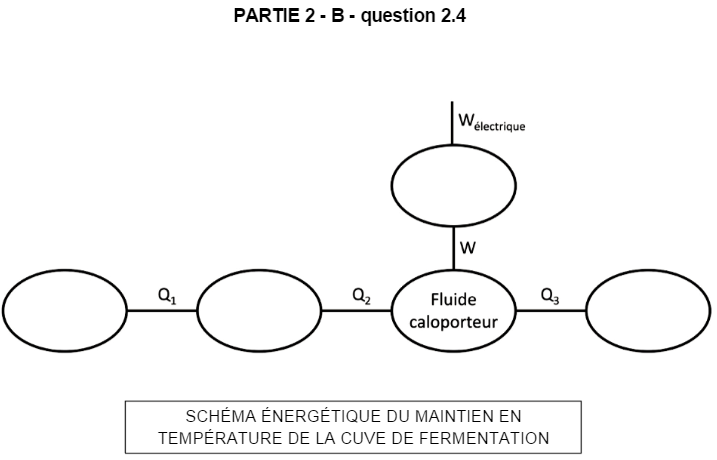
Le fluide caloporteur est déjà placé profitons en. On sait qu’on doit acheminé de l’électricité dans au moins l’un des appareil de la liste puisque nous pouvons lire : $\mathrm{W_{élec}}$. C’est un bel indice.
Un bassin d’eau ça consomme de l’électricité ? Pas terrible hein ? Pourquoi pas plutot le compresseur qui justement est une pompe qui achemine les fluides. Ça c’est sur que c’est un appareil qui fonctionne à l’électricité.
Maintenant il nous reste les positions :
Déjà celui qui réchauffe tout le système, c’est le plus grand. Qui englobe tout. La pièce en elle-même réchauffe forcément les appareils.
En ayant l’œil sur le document 3, on voit qu’après la cuve ce qui transporte la chaleur c’est le fluide caloporteur qui possède un sens de circulation. Et il va même passer par le compresseur avant le bassin d’eau. On sait exactement comment le circuit se boucle ainsi :
2.5 Évaluation du coût hebdomadaire du maintien en température de la cuve en négligeant l’énergie thermique libérée par la réaction de fermentation
2.5.1 Déduire de la question 2.3.1. la quantité d’énergie thermique $\mathrm{Q_1}$ apportée au contenu de la cuve pendant $\mathrm{1,0\;s}$ par le milieu extérieur.
Sachant que $\mathrm{t = 1\;s}$ :
2.5.2 On note $\mathrm{Q_2}$ l’énergie thermique cédée par la cuve de fermentation au fluide caloporteur. Sachant que la température intérieure de la cuve doit être constante, établir un lien entre les valeurs absolues des énergies thermiques $\mathrm{|Q_1|}$ et $\mathrm{|Q_2|}$. Justifier la réponse.
Nous avons tout à l’heure fait un schéma complet des arrivés et des sorties. On sait que $\mathrm{|Q_2|}$ ne dépend que de $\mathrm{|Q_1|}$… Donc on arrive, parce que la température est constante (pas d’évolution) :
2.5.3 Exprimer l’efficacité énergétique frigorifique $\mathrm{EEF}$ définie dans le document 3 en fonction des notations utilisées dans le schéma du document réponse en annexe. Vérifier que l’énergie électrique consommée par la machine pour maintenir l’intérieur de la cuve à $\mathrm{9,0°C}$ pendant $\mathrm{1,0\;s}$ est de l’ordre de $\mathrm{200\;J}$
Avec pour rappel :
Sur notre schéma, juste avant le fluide caloporteur nous avions $\mathrm{Q_2}$ :
Nous avons déjà croisé cet "énergie électrique consommée par la machine", c’était $\mathrm{W_{élec}}$ :
Maintenant que nous avons tout en main il suffit de réarranger :
L’ordre de $\mathrm{200\;J}$ est clairement respectés.
2.5.4 Calculer l’énergie nécessaire au maintien en température de la cuve pendant une durée d’une semaine, soit $7$ jours (durée de la première étape de fermentation). Sachant que l’on peut estimer le coût de $\mathrm{1\;kW.h}$ d’électricité à $0,145\;€$, calculer le coût financier du maintien de la cuve à $\mathrm{9,0°C}$ pendant $7$ jours
Commençons par le plus simple, combien d’heure ça fait, $7$ jours ?
Maintenant on va devoir comprendre combien de $\mathrm{Joules}$ notre machine consomme pour une certaine durée :
Il faut donc multiplier nos $\mathrm{204.3\;J}$ par le temps que l’on va exposer notre appareil :
Donc nous avons converti les joules en watts. Il suffit maintenant d’obtenir des kilowatts par heure :
|
$\mathrm{kW\cdot h}$ |
tarif en € |
|---|---|
|
$\mathrm{1\;kW\cdot h}$ |
$\mathrm{0.145\;€}$ |
|
$\mathrm{34.32\;kW\cdot h}$ |
$\mathrm{?}$ |
Produit en croix :
Soit près de $5\;€$ la semaine. A peine plus cher qu’un Döner Kebab :p.
2.5.5 En tenant compte de la réaction de fermentation qui a lieu à l’intérieur de cette cuve, discuter de la validité de l’estimation du coût financier du maintien de la cuve à $\mathrm{9,0°C}$ effectuée précédemment.
Lors d’un processus de fermentation avec des levures, nous avons l’obligation de respecter des normes. Si le protocole à été conçu de cette manière c’est que le maintiens à $\mathrm{9,0°C}$ été primordiale pour une fermentation contrôlée. De plus le système est largement peu onéreux… près de $5\;€$ la semaine ça reste viable sur le long terme !
Partie 3 - Le conditionnement de la bière
Énoncé : On s’intéresse dans cette partie à la mise en bouteille de la bière. Le système retenu pour contrôler le niveau de bière au remplissage de chaque bouteille est constitué d’une fibre optique dont le cœur est en $\text{polyméthacrylate de méthyle}$ (document $4$) parcourue par un faisceau laser ; l’extrémité de la fibre plonge dans le goulot de la bouteille. Le détecteur est sensible au flux énergétique renvoyé par l’extrémité de la fibre. Le remplissage est stoppé lorsque le niveau de liquide atteint la pointe de la fibre.
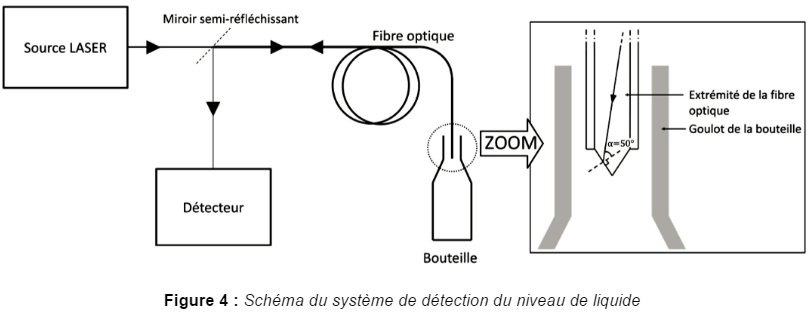
3.1 À l’aide des documents $4$ et $5$, préciser, en justifiant, la couleur de la lumière émise par la source laser.


Pour répondre à cette première question les deux documents sont obligatoire. Mais vous aurez en plus une équation à retrouver.
Dans le document $4$ vous trouvez la fréquence : $\mathrm{\nu = 4.75 \cdot 10^{14}\;Hz}$ Et vous devez savoir que l’unité réel (SI) des Hertz ($\mathrm{Hz}$) est en réalité : $\mathrm{s^{-1}}$
De cette fréquence nous allons devoir extirper une longueur d’onde ($\mathrm{nm}$) donc il va falloir convertir des $\mathrm{s^{-1}}$ en $\mathrm{nm}$ à l’aide de la célérité ($\mathrm{c}$) donné à la fin du document $5$.
Ce genre d’équation, je vous rassure, vous pouvez la retrouver simplement si vous ne vous en souvenez pas parfaitement. Via l’homogénéité des unités :
Bon vous le voyez il faut que la longueur d’onde néanmoins soit converti de $\mathrm{m}$ à $\mathrm{nm}$ à la fin de l’opération suivante :
Si l’on compare dans le tableau du document $5$ à quel couleur cela correspond, c’est un laser rouge.
3.2 Expliquer le principe de la propagation guidée de la lumière au sein d’une fibre optique. Une explication détaillée (sans calcul) du phénomène physique mis en jeu est attendue. Illustrer les quelques lignes d’explication par un schéma soigné et légendé du trajet d’un rayon lumineux dans la fibre optique (on pourra éventuellement s’aider des documents $4$, $6$ et $7$)

Le principe d’une fibre optique et d’obtenir un faisceau guidé, qui soit monochromatique, à travers un milieu permettant des réflexions (ici le $\mathrm{Plexiglass^{(R)}}$ aussi connu sous le nom de $\text{polyméthacrylate de méthyle}$). Avec pour rayon incident un angle particulier au delà de la valeur limite, angle rasant, cela permet d’éliminer les phénomènes de réfraction, seule la réflexion est possible au sein de la gaine.
Donc l’information transporté par le laser est transporté à la vitesse de la lumière sans perte de données (réfraction) et est réfléchis instantanément1 au point d’arrivé.
3.3 On s’intéresse au rayon arrivant à l’extrémité épointée de la fibre, lorsque celle-ci plonge dans la bière. À l’aide des documents $4$, $6$ et $7$, calculer l’angle $\mathrm{i_{lim}}$ d’incidence limite à l’interface fibre/bière.
Dans le cas où l’extrémité épointée de la fibre est dans l’air, l’angle d’incidence limite à l’interface fibre / air est de $42,5°$
On utilisa la très célèbre formule de Descartes : $\mathrm{n_{1}\sin (i_1) = n_{2} \sin (i_2)}$ (en faisant attention à utilisé le mode "dégrée" de votre calculette.)
- A l’interface fibre/air on a $\mathrm{i_{lim} = arcsin \left( \dfrac{1}{1,48} \right)} = 42.5°$.
- A l’interface fibre/air on a $\mathrm{i_{lim} = arcsin \left( \dfrac{1,34}{1,48} \right)} = 64.9°$.
$\mathrm{r}$ étant plus petit que l’angle d’incidence limite $64.9°$; il y a bien une réfraction en sortie de la fibre. Il n’y a pas de réflexion totale ici car $\alpha$ est plus petit que l’angle d’incidence limite $64.9°$.
-
A la vitesse de la lumière quoi, c’est déjà pas mal
 ↩
↩
Mon collègue, Holosmos, a proposé aujourd’hui de publier des corrections d’exercices de mathématiques. Cela m’a donné une idée, merci à lui pour l’initiative intéressante.
Les autres parties seront disponibles ici même au fur et à mesure.


