Maths en images #3

J’ai hésité à faire ce billet. Aujourd’hui, je ne vous présente pas un dessin portant sur un théorème ou une notion, mais un dessin plus personnel basé sur mes émotions.

Le dessin

Sans plus attendre, le voici.

De la topologie algébrique.

Légende

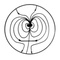
Des explications s’imposent, d’autant plus si je ne puis l’affilier à un résultat singulier. L’idée de ce dessin, c’était de faire ressentir la façon dont je vis la topologie algébrique.

En topologie, il est commun, presque naturel, de chercher à décomposer des objets et de chercher à les recoller. Mais ce recollement n’est pas toujours aisé [regardez ici comment on ne peut pas terminer la couture au centre du fait du retournement de la bande]. Et que ce soit aisé ou non, des choses intéressantes se produisent.

Dans le cas présent, j’ai voulu dessiner une bande de Möbius sur laquelle on essaye de coudre (plus joli que recoller pour un dessin) un simple plan. Cette couture est impossible globalement, du moins pas dans notre espace à 3 dimensions. (Si l’on cherchait à faire de jolies coutures, on pourrait par exemple voir que la bouteille de Klein est la couture de deux bandes de Möbius.)

Je terminerais par dire (sans beaucoup de détails malheureusement) que cette obstruction au recollement illustre aussi une construction subtile qui consiste en les classes d’obstruction primaire.

Si ce genre de dessins vous plait aussi, indiquez-le moi, j’en ai quelques autres en réserve … :-)

8 commentaires

Quand est-ce que tu as abordé la topologie pour la première fois Holosmos?

Et aussi, est-ce la même chose la topologie comme l’étude des déformations et celle comme l’étude des espaces avec des structures relatives à la continuité, aux voisinages, toussa?

+1 -0

Quand est-ce que tu as abordé la topologie pour la première fois Holosmos?

Il y a plus de trois ans maintenant

Et aussi, est-ce la même chose la topologie comme l’étude des déformations et celle comme l’étude des espaces avec des structures relatives à la continuité, aux voisinages, toussa?

On parle plutôt de topologie générale pour ces dernières notions. La topologie algébrique est l’étude introduite principalement par Henri Poincaré il y a plus d’un siècle. C’est d’ailleurs plutôt la topologie algébrique qui a motivé l’étude de la topologie générale afin de donner les outils nécessaires pour donner la rigueur aux intuitions de Poincaré (ses écrits étaient entachés d’erreurs).

C’est pas le même sujet bien qu’il y ait des liens évidents entre les deux parce que la topologie générale est essentielle dans toutes les branches des maths (absolument toutes). De mon point de vue, c’est plus un langage qu’un sujet d’étude, bien que ce soit incontournable.

+1 -0

Peut-on considérer la topologie générale comme fondement des mathématiques, au même titre que la théorie des ensembles ou des catégories?

Ozmox

Ce n’est pas un fondement parce que ça repose déjà sur autre chose de plus général (théorie des ensembles ou théorie des catégories, etc.). Il me faudrait détailler cette réponse, mais un logicien ne viendra probablement pas me contredire.

Et puis même si la topologie générale est présente dans toutes les branches, si on regarde plus précisément chaque sujet, il y a parfois des choses qui ne nécessitent pas de topologie. Par exemple tout ce qui se faisait avant le XXe.

En revanche, il y a aujourd’hui l’émergence d’une nouvelle fondation des mathématiques par la théorie homotopique des types. C’est une théorie qui a des liens très étroits avec la topologie algébrique (et non générale cette fois-ci) et qui peut être utilisée comme socle des mathématiques.

+1 -0

J’ai une autre question qui se détache un peu du contexte purement mathématique : pourquoi utilise-t-on la topologie en physique, lorsqu’on parle de relativité restreinte par exemple?

On utilise énormément la topologie générale et la topologie algébrique en physique ! Par exemple la théorie de jauge qui fournit le modèle standard des particules est entièrement basée sur des considérations de topologie algébrique.

Pourquoi, c’est une question très difficile à laquelle personne ne saura répondre sérieusement.

En revanche, ce que je peux dire, c’est que la topologie algébrique c’est un ingrédient clef quand on veut faire de la géométrie. Et la physique est évidemment une théorie géométrique. Que ce soit de la géométrie riemannienne pour la relativité ou de la théorie quantique des champs, les considérations topologiques sont incontournables.

+1 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte