Pour un petit robot, j’ai du réaliser un petit système localisant une personne qui parle dans l’espace avec un STM32F4, un raspberry pi et quelques micros.
- Récupérer le son
- Garder les sons utiles
- Dispositif de capture
- Calcul de l'angle de provenance
- Un angle smooth
Récupérer le son
Généralement, on trouve deux possibilités. La première est de localiser la personne après la capture du son et l’autre en même temps. Si on souhaite effectuer la localisation après, il faut juste penser à récupérer le son sur plusieurs canaux. Dans mon cas, il s’agissait de le faire en même temps que la personne parlait en traitant la sortie des micros (PCM 16 bits, 4 channels (un par micros), 48KHz). Ainsi, à l’entrée de mon algorithme, j’avais un petit tableau qui représentait les 4 micros et 0.2 secondes de son.
Garder les sons utiles
La seconde étape est de savoir si on souhaite localiser une personne sur cette entrée. Comme j’avais relativement peu de puissance (j’y reviendrais), je sommais juste les échantillons et je comparais la somme à un offset qui correspond à savoir si il y avait un bruit assez fort sur ces 0.2 seconde (plus, une seconde passe avec la Raspberry et une capture plus longue (1 seconde), mais le premier filtre marchait relativement bien).
Dispositif de capture
Tout l’algorithme tournait sur un STM32F4 qui comprenait aussi les 4 micros. La carte renvoyait sur la sortie SPI l’angle et le son capturé par les micros. Puis on pouvait au choix utiliser une raspberry ou une BeagleBone pour contrôler et afficher la STM, ou encore streamer le son. Pour localiser le son sur 180°, il suffit de 2 micros éloignés de quelques cm. On va donc partir du principe qu’on dispose de 2 micros.
Calcul de l'angle de provenance
Imaginons nous parler devant deux micros. L’un à 1 mètre devant nous, l’autre 1 mètre plus loin. Le son va alors partir de notre bouche, passer par le premier micro, puis par le second. Appellons cet écart $\Delta$. Ce qui nous donne :
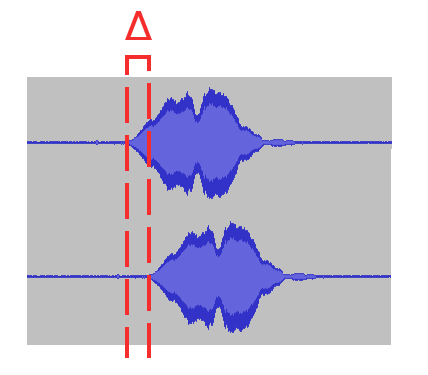
Cet écart, nous pouvons le calculer mathématiquement assez simplement avec ce qu’on appelle une cross-corrélation. $\Delta=min(\sum^{N-1}_{n=0}|x[n]-y[n-l]|^2)$ avec $x$ et $y$ nos deux canaux et $l$ les différents écarts possibles. On peut connaître $l_{max}$ à l’aide de notre fréquence d’échantillonage, de la vitesse du son dans l’air et de l’écart entre les deux micros $\Delta^*_{cm} = \Delta \times \frac{soundCel(cm/s)}{Frequency(frames/s)}$.
Ce qui nous permet d’obtenir notre angle de provenance $\theta$ sur 180° avec deux micros avec $\theta=\frac{acos(\frac{\Delta^*}{distanceMics})}{\pi \times 180}$

Note : 180°, car deux provenances donnent le même $\Delta$, imaginons un micro à 50cm à votre droite et un autre à 50cm à gauche, les deux vont recevoir le son en même temps.
Un angle smooth
Comme votre échantillonage est discret et non continu, l’angle en sortie sera lui-aussi discret. C’est-à-dire que vous n’aurez pas une précision infinie, surtout si vos micros sont très proches.
Il reste à régler deux problèmes. Le premier et que le moindre bruit peut fausser l’angle et donc on peut obtenir un angle qui change très vite du tout au tout. On peut améliorer le résultat en effectuant une moyenne pondérée de la valeur obtenue et des 10 précédentes valeurs, ce qui aura pour effet de smoother l’évolution de l’angle de provenance. Dans un second temps, sur des micros proches, il est possible d’ajouter des micros sans pour autant localiser dans des dimensions supérieures mais seulement pour en avoir un qui élimine les bruits à l’intérieur du robot et d’autres pour améliorer la précision de capture, comme le fait Alexa de Amazon pour localiser une personne à 360° avec 7 micros (6 en hexagone, 1 au centre pour éliminer les bruits interne je pense).
Pour ce petit projet, je me suis surtout heurté à des problèmes relatifs à l’embarqué. Vu que je touchais la limite de la puissance de calcul de la carte (pas en mémoire par contre), il y avait plein de fonctionnalités de C de base que je ne pouvais pas utiliser comme malloc, free, acos, qsort sans dépasser les limites de la carte et ne plus avoir le temps de communiquer les informations via le SPI. Par exemple, j’ai du réimplémenter acos mentionné plus haut pour qu’il prenne une division entière comme entrée qui me donnait l’indice d’un tableau en mémoire pour obtenir l’angle qui m’intéressait.
Mais au final, l’application fonctionnait.






