J’ai pris l’habitude de jouer une dizaine d’euros à chaque Vendredi 13 que je qualifie de perdu dès que je les joue. Aujourd’hui, j’ai eu le courage de réfléchir et d’aller chercher les informations pour répondre à la question : "Faut-il continuer à jouer ?" / "Pourrais-je avoir un gain de 10 000€ un jour ?".
- Combien de chance avons nous de gagner ?
- Pourrais-je avoir un gain de 10 000€ un jour ?
- Faut-il continuer à jouer ?
Combien de chance avons nous de gagner ?
Je suis allé sur le règlement du jeu EuroMillions pour trouver les chances de victoire page 19 que voici :
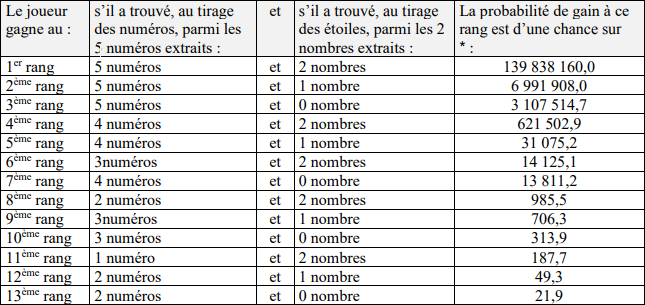
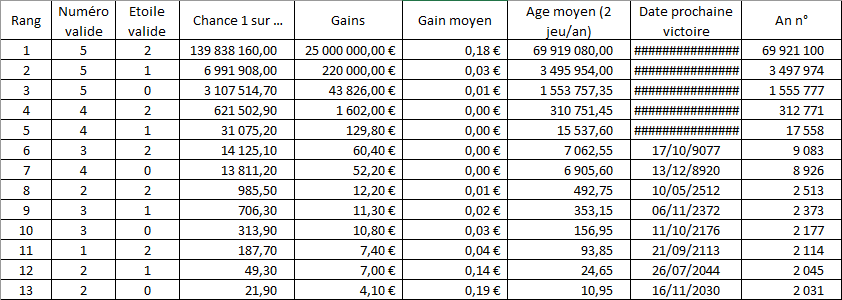
Ensuite j’ai regardé les répartition des gains pour ce tirage des derniers tirages et j’ai fais une moyenne basse pour obtenir ce tableau :
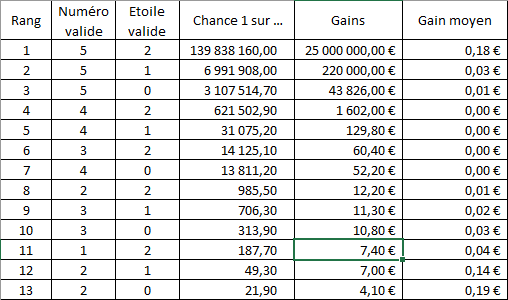
Ce qu’il faut comprendre (en prenant le rang 13 en exemple) c’est que pour gagner 4.10 €, vous avez 1 chance sur 22 jeu de gagner 4.10€ donc un gain un remboursement moyen par jeu de 0.19€. C’est-à-dire que vous perdrez à chaque jeu 2.31€ (= 2.5€ - 0.19€).
La probabilité de mourir dans un avion est estimé entre 12 à 16 millions. Si mourir en avion ne fait pas partie de vos peurs, gagner à l’Euromillions ne devrait pas faire partie de vos espérances.
Gagner le rang 1 équivaut à mourir une dizaine de fois en avion.
Pourrais-je avoir un gain de 10 000€ un jour ?
Quel est le remboursement moyen par jeu pour 10 000€ de gain ?
Le rang 3 (43 826€) à un gain remboursement moyen par jeu de 0.01€ en reprenant la colonne "Gain moyen" de mon précédent tableau.
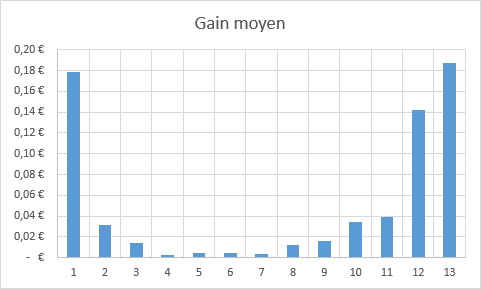
J’utilise le terme "Gain" dans mon graph mais le terme "Remboursement" est plus adapté.
Mes suppositions partent du principe que si j’ai 1 chance sur 20 de gagner, je gagnerais après le 20ème essais, ce qui n’est pas vrai dans la réalité, je peux très bien gagner au 1er essai comme au 39ème ou 52ème. Il me semble que c’est la loi Binomiale pour calculer la chance de gagner après X essais.
Quand pourrais je gagner plus de 10 000€ ?
Pour espérer gagner plus de 10 000€, en jouant à chaque tirage (2 fois par semaine) la moyenne est de 30 siècles.
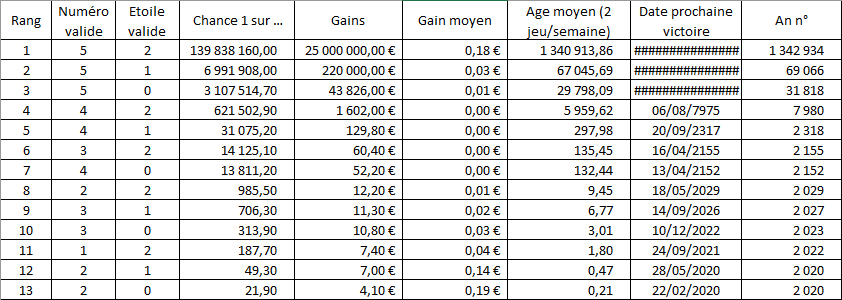
D’accord, et si on part sur un montant plus faible ? Par exemple, 1 000€.
Quand pourrais je gagner 1 000€ (rang 7) ?
En jouant à chaque tirage (2 fois par semaine), dans 132 ans le 13 avril 2152. Ce qui représente 260€ dépensé par an, soit au total 34 528€.

En jouant uniquement les Vendredi 13 soit environ 2 fois par an, je pourrais gagner le rang 7 après 7 siècles !
En jouant 5 numéros (= 12.5€) chaque Vendredi 13 soit 10 fois par an, je pourrais gagner le rang 7 le 19 février 3400.

Faut-il continuer à jouer ?
On dépense 2.5€ par jeu, il faut 22 jeux pour espérer gagner le premier palier de 4.10€ ! Ce qui représente un remboursement de 0.19€ par jeu. On dépense 2€50 pour essayer de gagner 20 centimes ! On gaspille donc 2€30 à chaque jeu.
Sans erreur statistique (c’est-à-dire que la victoire n’apparaît pas avant la moitié des jeux requis), je gagnerais 1 000 € (rang 7) en dépensant 12€50 chaque Vendredi 13 dans 1 300 ans.
Pour gagner le rang 7, j’ai besoin en moyenne de 13 811 essais, les 1 000€ de gain me rembourse seulement 400 jeux ! (1000 / 2.5 = 400).
Je joue mes 25€ par an en sachant que je les perdrais mais je me demande s’il n’y a pas meilleur investissement ou façon de les perdre. Comme par exemple : les placer dans une fontaine et faire un vœux.
Si j’ai fais une erreur dans mes calculs n’hésitez pas !



 Je pense que ça sera d’autant plus intéressant, étant donné le public de ZdS.
Je pense que ça sera d’autant plus intéressant, étant donné le public de ZdS.




 ).
).

