Des lentilles et des matrices

La première étape est donc de modéliser une interface sphérique. Pour coller à notre modèle linéaire, on veut extraire l’influence de la hauteur et de l’angle du rayon d’entrée. On va donc raisonner sur le schéma suivant.

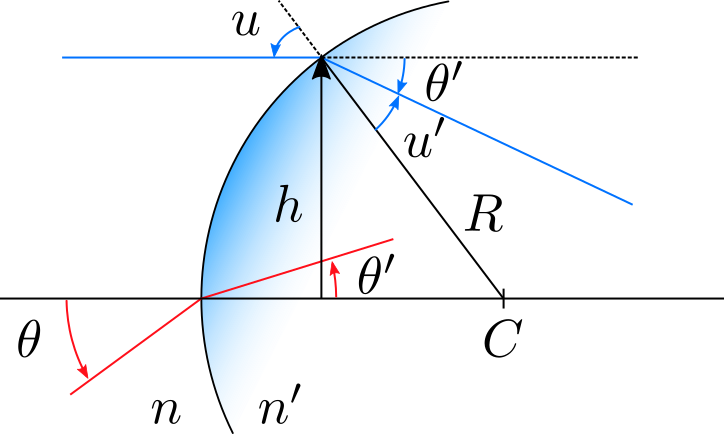
Pour arriver à nos fins on va supposer que le rayon $R$ de l’interface est très grand devant les distances considérées sur l’axe $\mathbf{\hat{z}}$ et devant $h$. Ceci permet de supposer que la hauteur du rayon ne va pas changer au passage de l’interface. Autrement dit, on connaît la première ligne de la matrice de l’interface $M_R$.

On se place également dans l’approximation des petits angles.

Ces hypothèses nous permettent de supposer qu’au point d’impact du rayon horizontal bleu sur l’interface, cette dernière est quasiment plane. On y applique la loi de Snell-Descartes dans l’approximation des petits angles.

Un peu de géométrie nous permet également d’avoir la relation suivante entre $\theta'$, $u'$ et $u$.

En combinant les deux on obtient une relation entre $u$ et $\theta'$.

$\textcolor{blue}{\theta'} = u\left(\frac{n}{n'}-1\right)$

Puisque d’autre part on a $u \approx \sin u = \frac{h}{R}$, on a finalement:

On traite également le rayon rouge. Ici une simple application de la loi de Snell-Descartes dans le cadre de nos hypothèses nous donne:

Dans le cadre de nos hypothèses (on parle d’approximation paraxiale), on a donc la matrice $M_R$ suivante, où la couleur rappelle l’origine de chaque expression :

Si vous êtes arrivés jusqu’ici, il est probable que vous ayez une bonne idée de ce que peut être une lentille. Cependant se poser la question va nous permettre d’en décrire une avec le formalisme que nous avons développé jusqu’ici. On va donc modéliser une lentille comme un matériau d’indice $n'$ et de longueur $L$ avec deux interfaces sphériques de rayons $R_1$ et $R_2$.

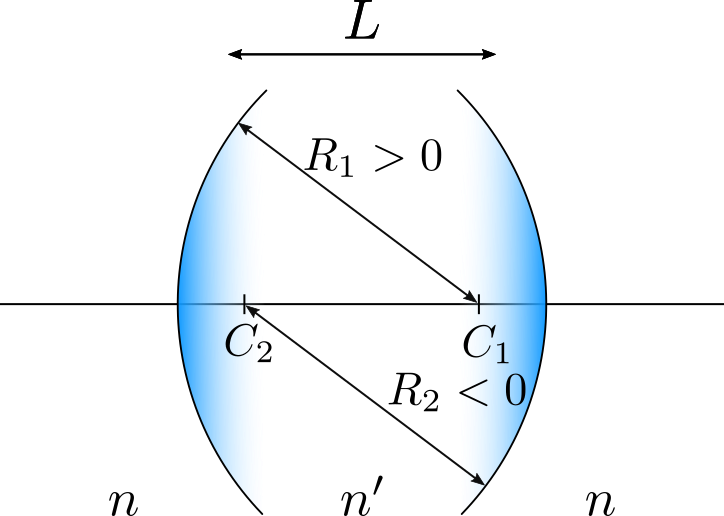
On peut maintenant essayer de déduire la matrice $M$ d’une lentille, paramétrée par $R_1$ et $R_2$ les rayons de ses interfaces, $n'$ l’indice de réfraction du matériau, $n$ l’indice de réfraction du milieu dans lequel est utilisée la lentille et $L$ l’épaisseur de la lentille.

On pourrait s’acharner à calculer cette matrice, mais il est plus utile de réaliser quelques approximations. Tout d’abord on va supposer que l’on peut parler de lentille fine. Autrement dit $L=0$. Ceci donne léquation suivante.

Il est ici utile de rappeler que le schéma utilisé pour raisonner représente les interfaces telles que $R_1>0$ et $R_2<0$. Ceci n’est absolument pas une hypothèse de notre calcul. Il existe des lentilles avec toutes sortes d’arrangements pour $R_1$ et $R_2$. Je porte par exemple des verres de lunettes dont les deux interfaces sont "dans le même sens".

On peut continuer à simplifier un peu notre expression pour $M$. Tout d’abord, vous le savez peut-être, on donne généralement $f$ la longueur focale d’une lentille. Ensuite on va utiliser notre lentille dans l’air, ce qui signifie que l’on peut supposer $n \approx 1$. $f$ vérifie ainsi :

On appelle ceci la Lens maker’s formula¹.

Ceci nous permet donc de simplifier encore l’écriture de $M$ pour arriver à la forme que nous utiliserons par la suite pour les lentilles minces.

C’est une formulation simple de l’effet du passage d’un rayon lumineux dans une lentille mince: le rayon est "tordu" proportionnelement à sa hauteur.

J’avais promis des applications, en voici une pour résoudre un problème commun d’optique géométrique : un système $2f$. Pour celleux qui n’ont jamais rencontré se montage (ou qui auraient oublié), c’est un montage avec deux lentilles séparées par la somme de leur distances focales. On raisonne sur le schéma suivant.

Ce genre de système permet de réaliser une lunette grossière : un objet à l’infini est grossi. Comment calculer ce grossissement ?

La première étape est de modéliser ce système.

Je n’ai pas besoin de modéliser la propagation en dehors du système puisqu’on utilise un objet à l’infini, donc des rayons parallèles à l’axe optique.

Ceci nous donne :

On a immédiatement le grossisement : un vecteur $V=\begin{pmatrix}h\\0\end{pmatrix}$ est transformé par le système en $V'=MV=\begin{pmatrix}- \frac{f_2}{f_1}h\\ 0 \end{pmatrix}$. On a donc agrandi l’objet d’un facteur $-\frac{f_2}{f_1}$. On peut remarquer que l’angle de sortie est mis à l’échelle par un facteur inverse de celui de hauteur. Autrement dit si on note $V=\begin{pmatrix}h\\ \theta\end{pmatrix}$ et $V'=MV=\begin{pmatrix}h'\\ \theta'\end{pmatrix}$, on a $h\theta=h'\theta'$. C’est un cas particulier de l’invariant de Lagrange, on peut y penser comme une condition de conservation de l’énergie.

Je pense que la plupart des gens qui souhaiteraient calculer rapidement la position d’une lentille mince pour imager un objet utiliseraient les fameuses formules de conjugaison. Mais peut-on retrouver ces formules avec l’approche matricielle ?¹

On considère le système suivant :

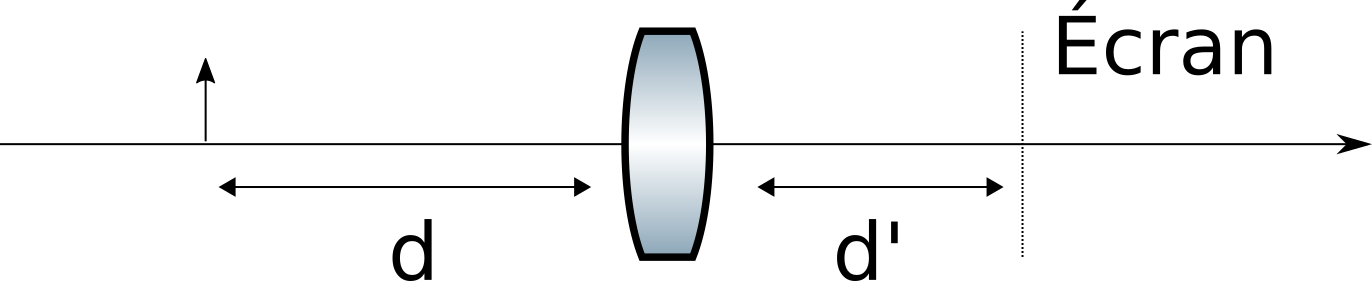
Notre objectif est donc de trouver $d$ et $d'$ afin de former une image sur l’écran. Il faut donc d’abord savoir ce que siginifie "former une image sur l’écran". En l’absence d’abbérations dans le système optique, on dit qu’une image est formée sur l’écran lorsque tous les rayons issus d’un point de l’objet se croisent au même endroit sur l’écran. Plus formellement, considérons le système est décrit par la matrice $M$ telle que:

Si le rayon $V=\begin{pmatrix}h\\ \theta\end{pmatrix}$ se présente en entrée du système, puisque le plan d’entrée est imagé sur le plan de sortie, alors le vecteur de sortie $V'=MV=\begin{pmatrix}h'\\ \theta'\end{pmatrix}$ est tel que $h'$ ne dépend pas de $\theta$. Pour cela il est nécessaire que $B=0$.

Cela nous permet donc d’avoir une condition sur la matrice $M$ pour former une image sur l’écran. Calculons $M$.

La condition $B=0$ peut donc être ré-écrite $d + d'\left( 1 - \frac{d}{f} \right) = 0$, ce qui s’écrit encore $\frac{1}{d'} + \frac{1}{d} = \frac{1}{f}$. Je vous laisse vous convaincre qu’avec la bonne convention de signe, on vient de retrouver la relation de conjugaison de Descartes.

Si maintenant on considère le même système, mais avec des distances labellisées légèrement différemment (figure suivante), on peut retrouver la relation de conjugaison de Newton.

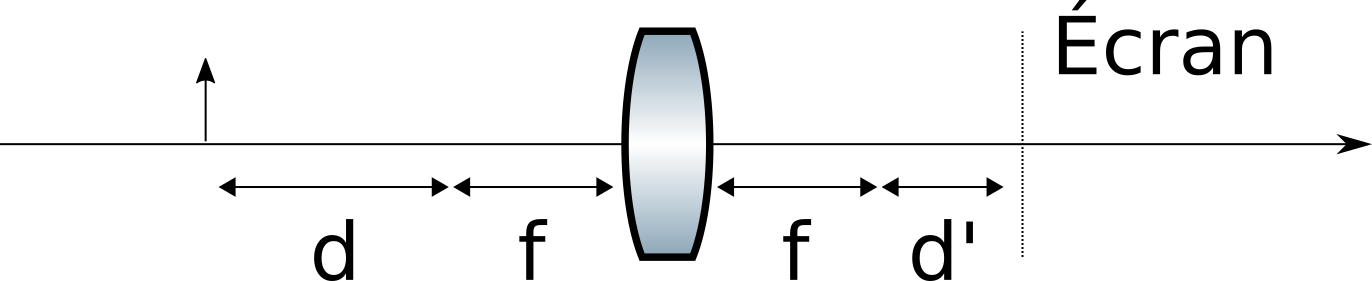
Calculons la matrice décrivant le système.

En appliquant la condition $B=0$ pour former une image,

À une convention de signe pour les distances près, on a bien retrouvé la formule de conjugaison de Newton.