Comment GCC optimise la mise à la puissance

Assembleur généré sans optimisation

GCC¹ génère de l’assembleur lisible à partir du code ci-dessus quand on lui demande gentiment à l’aide de la commande ci-dessous. Par défaut, le code sera généré sans optimisation.

gcc -S pow.c -o pow_noopt.s

La partie intéressante de la sortie est la suivante :

pushq	%rbp
.cfi_def_cfa_offset 16
.cfi_offset 6, -16
movq	%rsp, %rbp
.cfi_def_cfa_register 6
movsd	%xmm0, -8(%rbp)
movsd	-8(%rbp), %xmm0
mulsd	-8(%rbp), %xmm0
mulsd	-8(%rbp), %xmm0
mulsd	-8(%rbp), %xmm0
popq	%rbp
.cfi_def_cfa 7, 8
ret

Les lignes surlignées nous montrent qu’il y a 3 multiplications, et en regardant les registres utilisés, on déduit que le calcul qui est fait est $((x \cdot x) \cdot x) \cdot x$.

Assembleur généré avec optimisation

Demandons maintenant à GCC de refaire le travail mais en optimisant. Le niveau d’optimisation -O1 est suffisant pour ce billet, à condition d’autoriser en plus les optimisations non sûres, c’est-à-dire celles qui peuvent changer légèrement le résultat du calcul à cause des propriétés des nombres flottants².

gcc -S pow.c -o pow_opt.s -O1 -funsafe-math-optimizations

Le cœur du calcul est alors :

mulsd	%xmm0, %xmm0
mulsd	%xmm0, %xmm0
ret

Ce n’est plus le même calcul ! On n’a plus que deux multiplications, qui correspondent au calcul suivant : $x \cdot x \rightarrow y$ puis $y \cdot y \rightarrow x^4$. On a ainsi économisé une multiplication grâce au compilateur !

Obtenir les dumps des passes d’optimisation

Lors de la compilation GCC passe par des langages intermédiaires à partir desquels il fait certaines optimisations, notamment la représentation GIMPLE, proche du C et qui nous intéresse dans ce billet.

On peut observer le travail du compilateur en lui demandant des dumps de la représentation GIMPLE au fil des différentes passes d’optimisation. La commande est la suivante¹ :

gcc -S pow.c -o pow_opt.s -O1 -funsafe-math-optimizations -fdump-tree-all

On pourrait avoir encore plus de dumps avec l’option -fdump-rtl-all, qui rajoute toute une série de passe d’optimisations de plus bas niveau, sur une autre représentation utilisée plus en aval lors de la compilation.

Optimisation des puissances

Dans cette série de passes GIMPLE, GCC optimise les puissances en deux étapes :

1. la première consiste à remplacer les multiplications successives par une même valeur par une mise à la puissance builtin (c’est-à-dire powi), qui pourra être optimisée ensuite ;
2. une réécriture des mises à la puissance en termes de multiplications (et de manière optimale pour les plus petites).

Insertion de powi

Avant la passe 122, on a le code GIMPLE suivant :

pow4 (double x)
{
  double _1;
  double _2;
  double _4;

  <bb 2> [100.00%]:
  _1 = x_3(D) * x_3(D);
  _2 = _1 * x_3(D);
  _4 = _2 * x_3(D);
  return _4;

}

Après la passe 122, appelée reassoc1, qui correspond à l’étape 1 mentionnée ci-dessus, on voit la mise en place des puissances :

pow4 (double x)
{
  double _4;
  double reassocpow_6;

  <bb 2> [100.00%]:
  reassocpow_6 = __builtin_powi (x_3(D), 4);
  _4 = reassocpow_6;
  return _4;

}

En fait, c’est essentiellement comme si on avait compilé le code suivant, utilisant une builtin de GCC :

double pow4(double x)
{
  return __builtin_powi(x, 4);
}

Développement des puissances

Ensuite, cette builtin est redéveloppée sous forme de multiplications lors de la passe sincos ² :

pow4 (double x)
{
  double powmult_1;
  double powmult_4;
  double reassocpow_6;

  <bb 2> [100.00%]:
  powmult_1 = x_3(D) * x_3(D);
  powmult_4 = powmult_1 * powmult_1;
  reassocpow_6 = powmult_4;
  return reassocpow_6;

}

L’algorithme utilisé pour développer les puissances est optimal en termes de multiplications pour les petites puissances, les plus rencontrées en pratique.

On peut s’amuser à prendre un exemple un peu plus costaud, à savoir le calcul de $x^{91}$.

double pow91(double x)
{
    return __builtin_powi(x, 91);
}

Avec l’algorithme des multiplications successives par $x$, on aurait 90 multiplications. GCC s’en sort avec 9 :

pow91 (double x)
{
  double powmult_4;
  double powmult_5;
  double powmult_6;
  double powmult_7;
  double powmult_9;
  double powmult_10;
  double _13;
  double _15;
  double _16;

  <bb 2> [100.00%]:
  powmult_9 = x_1(D) * x_1(D);
  powmult_10 = x_1(D) * powmult_9;
  _16 = powmult_9 * powmult_10;
  _15 = powmult_10 * powmult_10;
  powmult_7 = _15 * _16;
  powmult_6 = powmult_7 * powmult_7;
  powmult_5 = powmult_6 * powmult_6;
  _13 = powmult_5 * powmult_5;
  powmult_4 = powmult_10 * _13;
  return powmult_4;

}

Cet algorithme forme successivement la puissance 2, 3, 5, 6, 11, 22, 44, 88, et enfin 91.

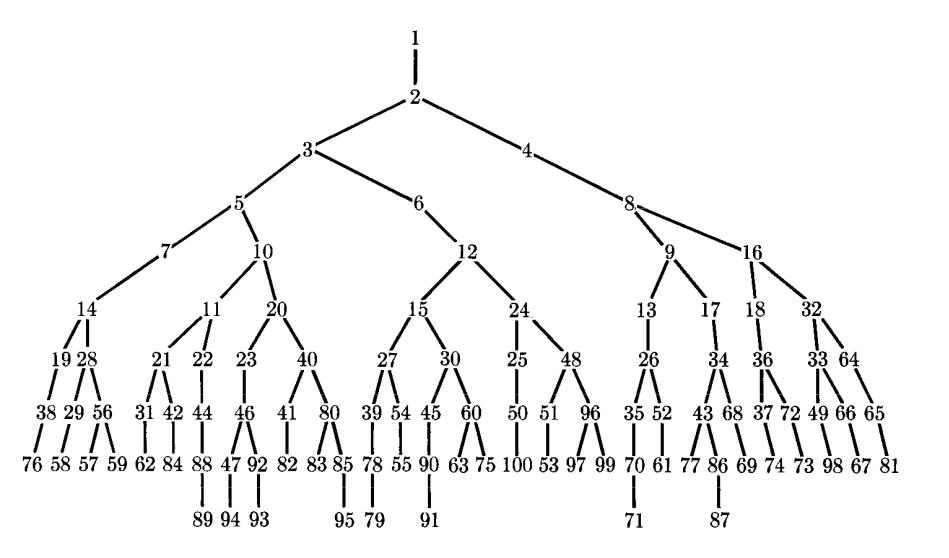
L’arbre optimal ci-dessous permet de vérifier que 9 est bien le nombre minimal d’étapes : pour 91, il y a 9 arêtes, chaque arête correspondant à une multiplication. On voit aussi qu’il existe plusieurs solutions : l’arbre ci-dessous ne forme pas les mêmes puissances que GCC.