Bonjour à tous !
Nous allons voir dans le très court billet comment savoir si deux tranches horaires se superposent.
Imaginons donc deux tranches horaires :
- La première qui va de A1 (heure de début) à A2 (heure de fin)
- Le seconde, qui va de B1 (heure de début) a B2 (heure de fin)
Comment feriez-vous ?
C’est facile ! Si B1 est entre A1 et A2, ou que B2 est entre A1 et A2, alors il y à supperposition !
C’est bien essayé, mais ce n’est pas tout à fait exact.
Si on fait un petit schéma, cette solution fonctionne dans les cas suivants :
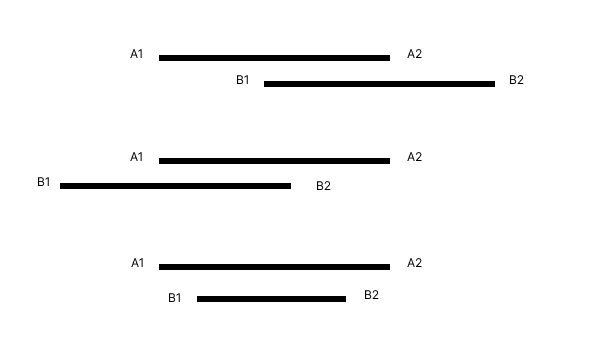
Mais cela ne fonctionne pas pour ce cas-ci, où les tranches horaires entrent pourtant en collision :
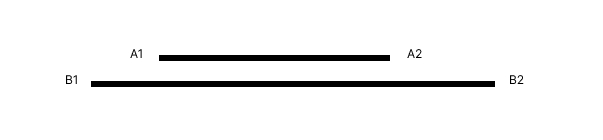
Afin de trouver la meilleure solution, faisons un schéma de tous les cas possibles.

Si on regarde ce schéma, on peut voir que dans les deux premiers cas, il n’y a pas de collision, alors qu’il y en a dans tous les autres cas.
Je vous propose donc de prendre le problème à l’envers : Faisons une conditions pour savour où il n’y à PAS de collision.
Il n’y a pas collision si la deuxième tranche horaire est trop à gauche de la première, ou trop à droite de la première.
Le pseudo-code associé serait donc :
SI B2 INFERIEUR A A1 OU QUE B1 SUPPERIEUR A A2 ALORS
PAS DE COLLISION
SINON
COLLISION
FIN
C’est bien joli tout ça, mais moi je voulais savoir quand il y avait collision !
Et bien nous avons juste à inverser la condition !
SI PAS (B2 INFERIEUR A A1 OU QUE B1 SUPPERIEUR A A2) ALORS
COLLISION
SINON
PAS DE COLLISION
FIN
Et voilà !
J’espère que cette petite astuce vous aura été utile !
Sachez également que cela fonctionne pour tester les collisions entre deux rectangles dans un jeu en 2D. Il suffit d’ajouter l’axe vertical dans la condition, et le tour est joué !




