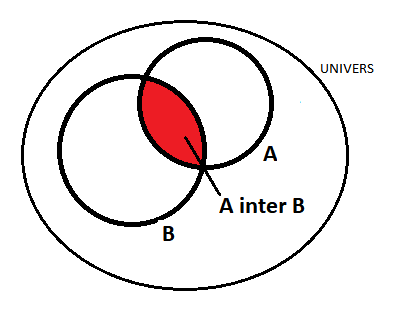
Intuition derrière la définition formelle de l'indépendance de deux évènement

a marqué ce sujet comme résolu.

Salut à tous,

dans un document que je lis, il est défini que deux évènements $A$ et $B$ sont indépendants si, et seulement si

$$P(A \cap B) = P(A)P(B).$$

Un des problèmes que me pose cette définition est que pour moi cette égalité est toujours vraie, mais je pense que c’est simplement parce qu’au collège/lycée on ne travaille qu’avec des évènements indépendants (surtout que j’ai déjà trouvé quelques contre-exemples donc bon).

Mais surtout le vrai problème c’est que je comprends par en quoi le fait que cette égalité soit respectée exprime que ces deux évènements ne s’influencent pas.

Merci d’avance pour vos réponses. :)

Édit : c’est l’intersection

+0 -0

C’est une intersection par contre ^^

$$ P(A \cap B) = P(A)P(B) $$

Attends je te fais le dessin qui donne l’intuition, deux secondes.

EDIT :

Dessin indépendance

La proportion qu’occupe A \cap B dans A est la même que la proportion qu’occupe B tout entier dans l’univers \Omega :

$$ \frac{P(A \cap B)}{P(A)} = \frac{P(B)}{P(\Omega)} $$

EDIT 2 : Sur mon dessin foireux, A et B ne sont pas du tout indépendants puisque ça se voit à l’œil nu que les proportions ne sont pas les mêmes, mais ça c’est parce que je suis une quiche. ^^

EDIT 3 : Du coup j’ai pas expliqué pourquoi c’est bien la notion naturelle d’indépendance : c’est parce que comme on a le respect des proportions que j’ai expliqué, pour $\omega \in \Omega$, si on sait que A est réalisé par $\omega$ ou pas (i.e $\omega \in A$ ou pas) ne change rien à la "chance" d’avoir $\omega \in B$.

Je sais pas si j’ai été clair, d’autant que mon dessin est pas très réussi. Tu as compris ?

+0 -0

Sans dessin, pour avoir l’intuition, il faut plutôt se poser la question pour deux évènements dépendants. Si $B$ dépend de $A$, une fois qu’on a fait $A$ – disons que si $A$ est vrai, on a beaucoup de chances que $B$ soit vrai – on a plus de chance de faire $B$ donc $P(A \cap B)$ sera plus grand que $P(A)P(B)$. Réciproquement si quand $A$ est vrai on a beaucoup de chances que $B$ soit faux, alors $P(a \cap B)$ sera plus petit que $P(A)P(B)$. On a deux cas extrêmes,

  • celui où $A = B$, on a $P(A \cap A) = P(A)$ ;
  • celui où $A = \overline{B}$, on a $P(A \cap B) = P(\varnothing)$.
+1 -0

Moi je vois cette formule comme quoi la probabilité de A sachant B, pour A et B indépendants, est égale à la probabilité de A. En somme cette dernière n’est pas affectée par B.

Idem inversement. Mais ça dépend de la manière dont ton cours est construit.

Ozmox

Cela repousse juste le problème d’intuition : "pourquoi la probabilité de B sachant A serait $\frac{P(A \cap B)}{P(A)}$ ?"

+0 -0

Quand on parle de probabilité, et d’événements indépendants ou non, je pense toujours aux exercices de base en probabilité : les exercices avec des dés.

Je lance 2 dés. Quelle est la probabilité que le 1er dé donne un nombre impair, quel est la probabilité que le 2ème dé donne un nombre impair, quelle est la probabilité que les 2 dés donnent des nombres impairs : on a 2 dés indépendants… tout va bien. 50% pour le 1er dé, 50% pour le 2ème dé, et 50%*50% pour le couple de dés.

Je lance maintenant un seul dé. J’ai 2 événements :

  • A = le dé sort un nombre pair.
  • B = le dé sort un nombre petit (1,2 ou 3)

Comme je lance un seul dé, on se doute que les événements sont dépendants (ce n’est pas une certitude)… et les calculs le confirment.

+0 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte