Bonjour à tous,
Aujourd’hui, je viens vous proposer une petite activité pour occuper ces longs mois de vacances pour ceux qui ont la chance d’encore en avoir : la construction d’un analemme.
Qu’est-ce qu’un analemme ?
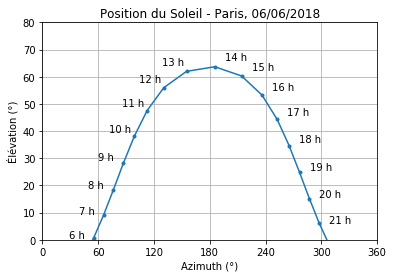
Vous savez déjà que le soleil bouge dans le ciel. Ou tout au mojs, semble bouger. Il se lève d’un coté, se couche de l’autre, va plus haut en été qu’en hiver, etc.
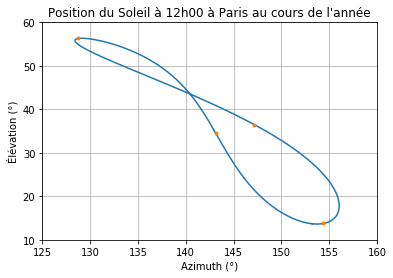
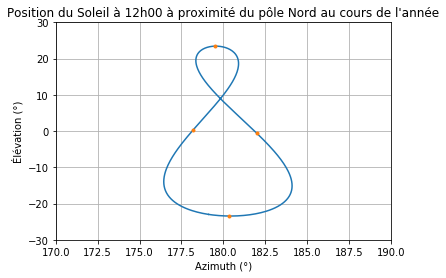
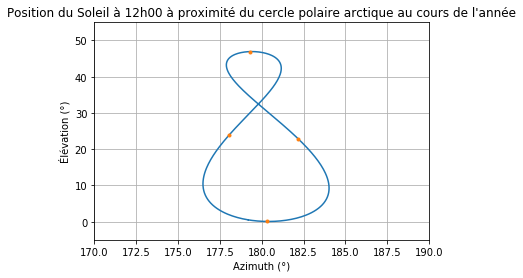
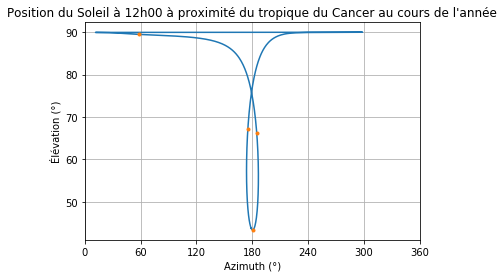
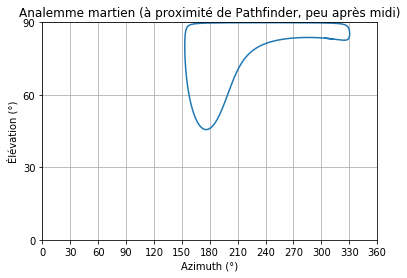
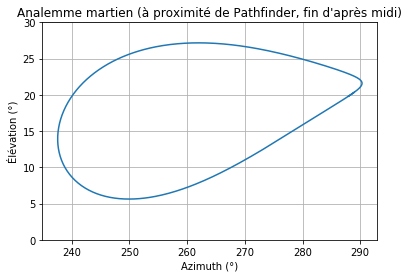
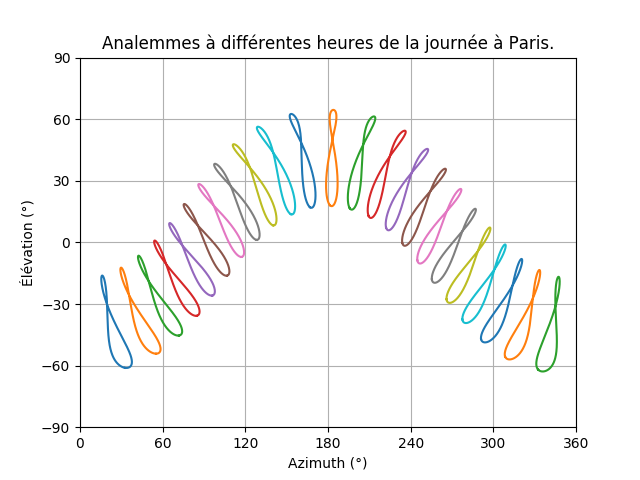
Ce que vous ne savez peut-être pas, c’est que si vous comparez la position du Soleil à la même heure tous les jours pendant un an, on obtient une forme de "8". Une petite photo juste en dessous.

Quel est le but de l’atelier ?
Il y en a deux :
- Le premier sera de comprendre d’où cet effet vient. De manière complètement fortuite, ça me permet aussi d’écrire beaucoup moins d’explication dans ce sujet initial.
- Le second sera d’écrire un programme qui permette de donner la position du Soleil dans le ciel à n’importe quel jour et heure, et n’importe quel endroit.
Il sera bien entendu possible d’approfondir. Quand je l’avais fait, j’avais calculé le nombre maximal d’heures d’ensoleillement derrière un mur pendant une année par exemple.
Prérequis
Selon le niveau de précision que vous voulez, ils peuvent être très bas. En gros, vous aurez besoin des trois relations trigonomètriques reliant cos, sin et tan aux longueurs des cotés d’un triangle. Et ce sera tout.
Pour vous guider un peu
Si vous voulez y réfléchir par vous même, ne lisez pas cette section. Mais même si vous la lisez, vous n’y trouverez pas toutes les réponses.
L’origine de l’analemme vient de la différence entre l’heure solaire et l’heure de nos montres. Le Soleil n’est pas toujours au plus haut à midi exactement. Calculer la différence va vous faire arriver sur "l’equation du temps".
Il y a deux phénomènes principaux à prendre en compte (mais selon le degré de raffinement souhaité, vous pouvez en prendre davantage) :
- l’orbite de la Terre autour du Soleil n’est pas circulaire, mais elliptique
- et les plans de la rotation autour du Soleil et de la rotation de la Terre sur elle-même ne sont pas les mêmes.
C’est à vous !
Maintenant, y’a plus qu’à ! Si vous avez des questions, n’hésitez pas. Si je vois que ça bloque, je posterai des schémas pour aider. En espérant que ça vous intéresse !